Файл: Алгебра жне анализ бастамалары сабатарында физикалы мазмнды тапсырмаларды олдануды Тсілдері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 20
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ӘОЖ 37,016:51:531,26
«АЛГЕБРА ЖӘНЕ АНАЛИЗ БАСТАМАЛАРЫ» сабақтарында физикалық мазмұнды тапсырмаларды қолданудың ТӘСІЛДері
Шымкент университеті
П.ғ.к., аға оқытушы Утебаева Ш.К, магистр оқытушы Таджиханова К.И.
В этой статье рассматривается
Алгебра және анализ бастамаларында негізгі тараулардың бірі - “Интеграл”. Мұнда Ньютон-Лейбниц формуласын пайдаланып физикалық мазмұнды есептер шығарту мүмкіндігі мол. Сонда оқушылар “алғашқы функцияны табу”, “интегралдау шектері”, “шек”, “қосынды таңбасы” сияқты ұғымдарды өздеріне таныс нақты құбылыстар арқылы түсіну мүмкіндігін пайдалана алады. Мұнда физикалық процестерді талдау кезде міндетті түрде математикада үйренген ережелерді басшылыққа ала отырып, физикалық тұрғыдан ойлауға үйрету керек. “Қисық сызықты трапецияның ауданы” тақырыбы өтілгеннен кейін, оқушыларға “Айнымалы күштің жұмысын” есептеп табу тапсырмасын беруге болады.
Талдау жобасы мынадай болуы мүмкін. Айталық, координата өсіндегі
болады.
Сонда i бөліктегі
Сонда теоремаға сәйкес
Мысалы: Бұрамалы серіппенің хсығылу күші
Шешуі:
немесе
10-11 сыныптың “Алгебра және анализ бастамалары” пәніндегі қарастырылатын мәселелерді шартты түрде екі топқа бөлуге болады:
-
1.Туынды. Туындыны түрлі функциялар (тригонометриялық, дәрежелік, көрсеткіштік және логарифмдік) зерттеуге қолдану. -
2.Интеграл. Интегралды есептеулерде қолдану.
Енді міне осы топтар бойынша, негізгі тарауларды оқып-үйрену кезінде оларды физикамен байланыстыра отырып оқушы шығармашылығын дамыту жолдарын қарастырайық.
1. Физикадағы лездік жылдамдық, лездік үдеу, орын ауыстыру, лездік қуат, шек ұғымдары математикадағы туынды, алғашқы функция, интеграл ұғымдарын байланыстыра оқыту бұл ұғымдардың оқушылардың дұрыс қабылдауына мүмкіндік туғызады. өйткені бұл ұғымдар математикада қатаң абстракты ұғымдар түрінде берілсе, физикада көрнекі-бейнелік түрде қабылдау мүмкіндігі бар. Шын мәнінде математикада бұл ұғымдар қалыптастырылу барысында физикалық құбылыстар мысалға келтіріледі. Физиканың негізгі заңдары туынды, дифференциал, интеграл түрінде жазылғанда өзінің қатаңдығын сақтайды (Ньютонның екінші заңы, электромагниттік индукция заңы, тартылыс өрісіндегі жұмыс, тепе-теңдіктің түрлері т.б) [1].
Осы тұрғыдан алғанда, физикалық және математикалық функционалдық тәуелділіктерді анықтаудың ортақ алгоритмдік сұлбасын жасаған дұрыс. Мысалы, туынды көмегімен физикалық ұғымды анықтаудың жалпы сұлбасы төмендегідей болуы мүмкін: [2].
-
Туынды ұғымын қолдануға болатындығына көз жеткізгеннен кейін функционалдық тәуелділікті y=f(x) түрінде жазып алу; -
Функцияның орташа өзгеру жылдамдығын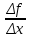 түрінде табу;
түрінде табу; -
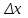
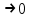 жағдайында функцияның шекті
жағдайында функцияның шекті 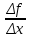 мәнін f'(x)=
мәнін f'(x)=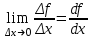 түрінде жазу;
түрінде жазу; -
Мынадай тізбек бойынша физикалық шаманың анықтамасын тұжырымдау: берілген функциядан алынған туынды бойынша анықталған физикалық ұғымның аты, функцияның атауы, аргумент атауы, т.б.
Ал интеграл арқылы физикалық ұғымды анықтауда мына ретті сақтауға болады (мұнда интегралдаудың дифференциалдауға кері амал ескеріледі).
5.Сәйкес келетін аргументі бойынша ізделінді функцияның туындысын, мысалы
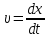 түрінде жазу;
түрінде жазу; 6.Алғашқы функциясы, мысалы x=
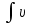 dt бойынша функцияны анықтау;
dt бойынша функцияны анықтау;-
Аргументтің сәйкес мәндері бойынша, ізделінді функцияның өзгерісін табу, мысалы х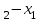 =
=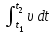 интегралы түрінде, содан кейін физикалық шаманың анықтамасын тұжырымдау. Мұндай ортақ тәсілмен жүргізілген жұмыстар оқушылардың жоғарыда аталған ұғымдарды дұрыс меңгеріп, оларды шығармашылық тапсырмаларды орындауда тиімді пайдаланатындығын тәжірибе көрсетіп берді.
интегралы түрінде, содан кейін физикалық шаманың анықтамасын тұжырымдау. Мұндай ортақ тәсілмен жүргізілген жұмыстар оқушылардың жоғарыда аталған ұғымдарды дұрыс меңгеріп, оларды шығармашылық тапсырмаларды орындауда тиімді пайдаланатындығын тәжірибе көрсетіп берді.
Физикадағы лездік жылдамдық, лездік үдеу шамаларын радиус-вектордан уақыт бойынша алынған туындысына тең деп, мынадай белгілеулер енгізіледі
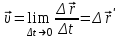 [2]. Бұдан ары қарай оның мағынасына талдау жасалмайды. Енді математикада осы ұғымды оқушылармен кеңірек талдауға болады. Айталық, әйтеуір бір нүкте АВ қисық сызық бойымен қозғалсын (1-сурет).
[2]. Бұдан ары қарай оның мағынасына талдау жасалмайды. Енді математикада осы ұғымды оқушылармен кеңірек талдауға болады. Айталық, әйтеуір бір нүкте АВ қисық сызық бойымен қозғалсын (1-сурет). 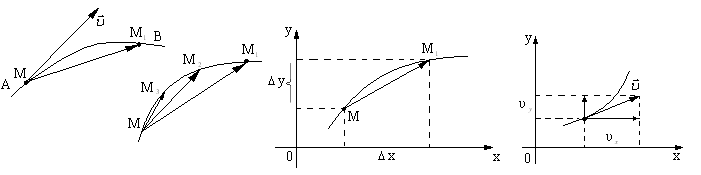
1 - сурет 2 - сурет 3 - сурет 4 - сурет
Нүктенің t және (t+
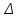 t) уақыттағы орындары М және М
t) уақыттағы орындары М және М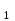 болсын. Сонда
болсын. Сонда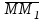 векторы
векторы 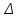 t уақыт ішіндегі дененің орын ауыстыруын көрсетеді. Физикада
t уақыт ішіндегі дененің орын ауыстыруын көрсетеді. Физикада 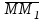 =
=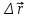 (радиус вектор өзгерісі),
(радиус вектор өзгерісі), 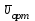 - векторлық шама
- векторлық шама 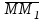 орын ауыстыруының
орын ауыстыруының 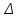 t уақыт аралығына қатынасымен анықталып, нүктенің орташа жылдамдығын анықтайды
t уақыт аралығына қатынасымен анықталып, нүктенің орташа жылдамдығын анықтайды 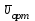 =
=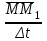 .
. 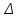
t- оң скаляр шама болғандықтан,
 векторы
векторы  векторымен бағыттас болады. Уақыт аралығының азаюына қарай ММ орын ауыстыруының модулі де бағытында өзгереді (2-сурет).
векторымен бағыттас болады. Уақыт аралығының азаюына қарай ММ орын ауыстыруының модулі де бағытында өзгереді (2-сурет). 
 ұмтылғанда, М
ұмтылғанда, М нүктесі М нүктесіне шектеусіз жақындайды, сонда
нүктесі М нүктесіне шектеусіз жақындайды, сонда 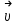 =
=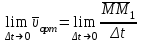 . Бұл шек, нүктенің М нүктесіндегі лездік жылдамдығын анықтайды, ал оның бағыты М нүктеге жүргізілген жанама бағытымен сай келеді. Енді нүкте қозғалысын ХОУ координата жазықтығында қарастырайық. Қозғалыс x=f
. Бұл шек, нүктенің М нүктесіндегі лездік жылдамдығын анықтайды, ал оның бағыты М нүктеге жүргізілген жанама бағытымен сай келеді. Енді нүкте қозғалысын ХОУ координата жазықтығында қарастырайық. Қозғалыс x=f (t) және y=f
(t) және y=f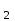 (t) теңдеулермен берілсін (3-сурет).
(t) теңдеулермен берілсін (3-сурет). Сонда
 векторы
векторы  t уақыт ішіндегі орын ауыстыру болсын. Енді
t уақыт ішіндегі орын ауыстыру болсын. Енді  векторын координата өстеріне проекциялайық, сонда (
векторын координата өстеріне проекциялайық, сонда ( )
)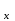 =
= , (
, (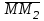 )
)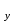 =
=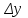 дейік.
дейік.  =
= екендігі белгілі, онда (
екендігі белгілі, онда ( )
)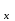 =
=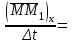
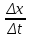 және
және 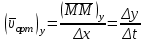 .
. 
