19-21 (19 – базовый уровень, 20 – повышенный уровень,
21 – высокий уровень, время – 6 + 8 + 11 мин)

Тема: Теория игр. Поиск выигрышной стратегии.

Что проверяется:

Умение анализировать алгоритм логической игры. Умение найти выигрышную стратегию игры. Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию.

1.5.2. Цепочки (конечные последовательности), деревья, списки, графы, матрицы (массивы), псевдослучайные последовательности.

1.1.3. Умение строить информационные модели объектов, систем и процессов в виде алгоритмов.

Что нужно знать:

• 
  в простых играх можно найти выигрышную стратегию, просто перебрав все возможные варианты ходов соперников
  
• 
  для примера рассмотрим такую игру: сначала в кучке лежит 5 спичек; два игрока убирают спички по очереди, причем за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку
  
• 
  первый игрок может убрать одну спичку (в этом случае их останется 4), или сразу 2 (останется 3), эти два варианта можно показать на схеме:
  

• 
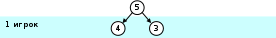
  если первый игрок оставил 4 спички, второй может своим ходом оставить 3 или 2; а если после первого хода осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну:
  

• 
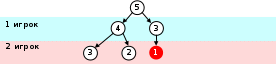
  если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом:
  

• 
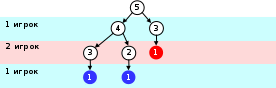
  простроенная схема называется «деревом игры», она показывает все возможные варианты, начиная с некоторого начального положения (для того, чтобы не загромождать схему, мы не рисовали другие варианты, если из какого-то положения есть выигрышный ход)
  
• 
  в любой ситуации у игрока есть два возможных хода, поэтому от каждого узла этого дерева отходят две «ветки», такое дерево называется двоичным (если из каждого положения есть три варианта продолжения, дерево будет троичным)
  
• 
  проанализируем эту схему; если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока
  
• 
  кто же выиграет при правильной игре? для этого нужно ответить на вопросы: 1) «Может ли первый игрок выиграть, независимо от действий второго?», и 2) «Может ли второй игрок выиграть, независимо от действий первого?»
  
• 
  ответ на первый вопрос – «да»; действительно, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу
  
• 
  ответ на второй вопрос – «нет», потому что если первый игрок сначала убрал одну спичку, второй всегда проиграет, если первый не ошибется
  

---

• 
  таким образом, при правильной игре выиграет первый игрок; для этого ему достаточно первым ходом убрать всего одну спичку
  
• 
  в некоторых играх, например, в рэндзю (крестики-нолики на бесконечном поле) нет выигрышной стратегии, то есть, при абсолютно правильной игре обоих противников игра бесконечна (или заканчивается ничьей); кто-то может выиграть только тогда, когда его соперник по невнимательности сделает ошибку
  
• 
  полный перебор вариантов реально выполнить только для очень простых игр; например, в шахматах сделать это за приемлемое время не удается (дерево игры очень сильно разветвляется, порождая огромное количество вариантов)
  
• 
  все позиции в простых играх делятся на выигрышные и проигрышные
  
• 
  выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
  
• 
  если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
  
• 
  выигрышные и проигрышные позиции можно охарактеризовать так:
  

• 
  позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
  
• 
  позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию - выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
  

---

Пример задания:

P-02(демо-2023).Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит

куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 129 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 128.

Задание 19.

Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Задание 20.

Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

− Петя не может выиграть за один ход;

− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Задание 21

Найдите значение S, при котором одновременно выполняются два условия:

– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Решение (программа, автор разбора А. Кабанов, идея – И. Воропаев, доработка – А. Кабанов и К. Поляков).

1. 
   Напишем функцию, которая определяет существование выигрышной стратегии не более чем за m ходов обоих игроков. Функция имеет два параметра: количество камней S и наибольшее возможное количество ходов m. С каждым ходом значение m уменьшается на 1, показывая тем самым оставшееся число ходов до необходимого окончания игры:
   

def f(s,m):

if s>=129: return m%2==0 #1

if m==0: return 0 #2

if m%2!=0:

return f(s+1,m-1) or f(s*2,m-1) #3

else:

return f(s+1,m-1) and f(s*2,m-1) #4

---

2. 
   При завершении игры функция отмечает победными такие варианты игры, в которых игра закончилась ровно за m ходов или менее, но тем же игроком (оставшееся значение m чётно) (#1).
   
3. 
   Варианты, требующие большей глубины, чем m, отбрасываются (#2).
   
4. 
   Если оставшееся число ходов нечётно, то для победы достаточно существования стратегии в одном из следующих ходов (#3). В противном случае стратегия должна быть во всех ходах (#4). Так происходит, потому что нечётное количество ходов подразумевает победу игрока, выполняющего ход из этой позиции. Тогда как чётное количество ходов подразумевает гарантированную победу его противника.
   
5. 
   Для нахождения ответа на 19 задание найдём значение S, для которого существует выигрышная стратегия за 2 хода
   

print( '19)', *[s for s in range(1,129) if f(s,2)] )

6. 
   Для нахождения ответа на 20 задание найдём значения S, для которых не существует выигрышной стратегии за 1 ход, но существует за 3 хода.
   

print( '20)', *[s for s in range(1,129) if not f(s,1) and f(s,3)] )

7. 
   Для нахождения ответа на 21 задание найдём значение S, для которого не существует выигрышной стратегии за 2 хода, но существует за 4 хода.
   

print( '21)', *[s for s in range(1,129) if not f(s,2) and f(s,4)] )

8. 
   Ответ:
   

19) 64

20) 32 63

21) 62

Ещё пример задания:

P-01(демо-2022).Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит

куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 29 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 28.

Задание 19.

Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Задание 20.

Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

− Петя не может выиграть за один ход;

− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Задание 21

Найдите значение S, при котором одновременно выполняются два условия:

---

– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Решение (построение таблицы).

9. 
   задачи с одной кучей просто решаются с помощью таблицы (массива); будем записывать в ячейках таблицы числовую оценку позиции: положительное число N означает выигрыш за Nходов, отрицательное число (–N) – проигрыш за N ходов
   
10. 
    очевидно, что при всех S ≥ 15 Петя выигрывает свои первым ходом, увеличив количество камней в куче вдвое; это позиции с оценкой 1 (выигрыш в один ход):
    

    1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	...
    														1	1	1

11. 
    все возможные ходы из позиции 14 (это 15 и 28) ведут в позиции с оценкой 1, то есть 14 – проигрышная позиция с оценкой –1: проигрыш за один ход (Петя, начинающий игру, может ходить любым способом, но Ваня своим первым ходом сразу сможет выиграть):
    

    1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	...
    													–1	1	1	1

12. 
    гарантированный выигрыш за 2 хода возможен для тех позиций, из которых есть ход в позицию с оценкой –1, то есть, из позиций 13 и 7; оценка этих позиций – 2:
    

    1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	...
    						2						2	–1	1	1	1

13. 
    дальше определяем все позиции, откуда все ходы ведут в позиции с оценкой 1 или 2 (все они уже заполнены в таблице); определяем, что это только позиция 12 (возможные ходы – 13 с оценкой 2 и 24 с оценкой 1):
    

---

Смотрите также файлы

• Экология мірді соып тран жрегі!.docx

• ТАырып Инвестициялы саясат туралы ым Инвестицияны экономикалы мазмны мен рлі Инвестиция термині латынны invest сзінен аударанда салым салу.docx

• Балаларды жасы 5 жас Жоспар андай кезеге жасалды (айды, жылды крсету).docx

• Математическая грамотность (8 класс) Характеристики заданий и система оценивания.docx

• Бастауыш, ши бауырса, самса мелкие, булочки мелкие, жеті нан.docx