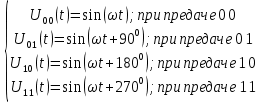Файл: Цель работы изучить основные способы увеличения энтропии дискретного источника и принципы эффективного кодирования. Домашнее задание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.12.2023
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Цель работы: изучить основные способы увеличения энтропии дискретного источника и принципы эффективного кодирования.
Домашнее задание
| N | p(A) | p(M) | p(A/A) | p(M/A) | p(A/M) | p(M/M) |
| 1 | 0.15 | 0.85 | 0.2 | 0.8 | 0.1 | 0.9 |
-
Задан дискретный источник двоичных сообщений, который производит слова, состоящие из двух букв А и М. Всего возможно четыре различных сообщения, слова: АА, АМ, МА, ММ. Рассчитайте вероятности p(AА), p(АМ), p(MA), p(ММ), если заданы безусловные вероятности p(А), p(М) и условные вероятности p(А/М) – вероятность буквы А, если первой в слове была буква М и т.д.
Вычислим вероятности каждого слова из двух букв
p(AA)=p(A)*p(A/A)=0.15*0.2=0.03
p(AM)=p(A)*p(M/A)=0.15*0.8=0.12
p(MA)=p(M)*p(A/M)=0.85*0.1=0.085
p(MM)=p(M)*p(M/M)=0.85*0.9=0.765
-
Рассчитаем энтропию источника H и его избыточность R.
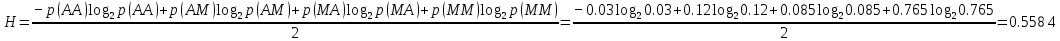
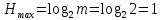
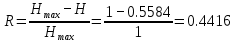
-
Закодируем слова четверичным кодом и рассчитаем его энтропию и избыточность.
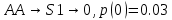
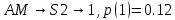
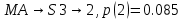
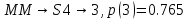
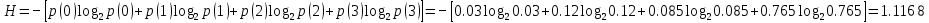
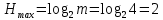
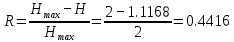
-
Закодируем четыре слова безызбыточным кодом с префиксными свойствами, построив кодовое дерево. Рассчитаем энтропию нового двоичного кода, его избыточность и среднюю длину кодовой комбинации.
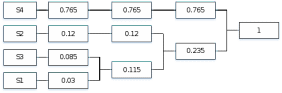
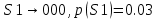
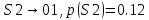
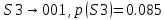
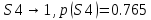
Вычислим вероятности 0 и 1 в кодовых комбинациях двоичного кода:
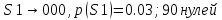
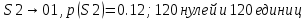
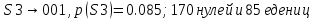
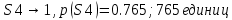
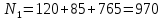
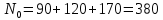
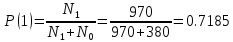
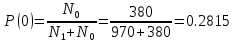
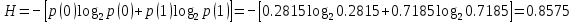

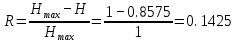
Рассчитаем среднюю длину кодовой комбинации:
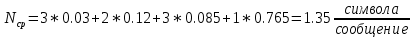
-
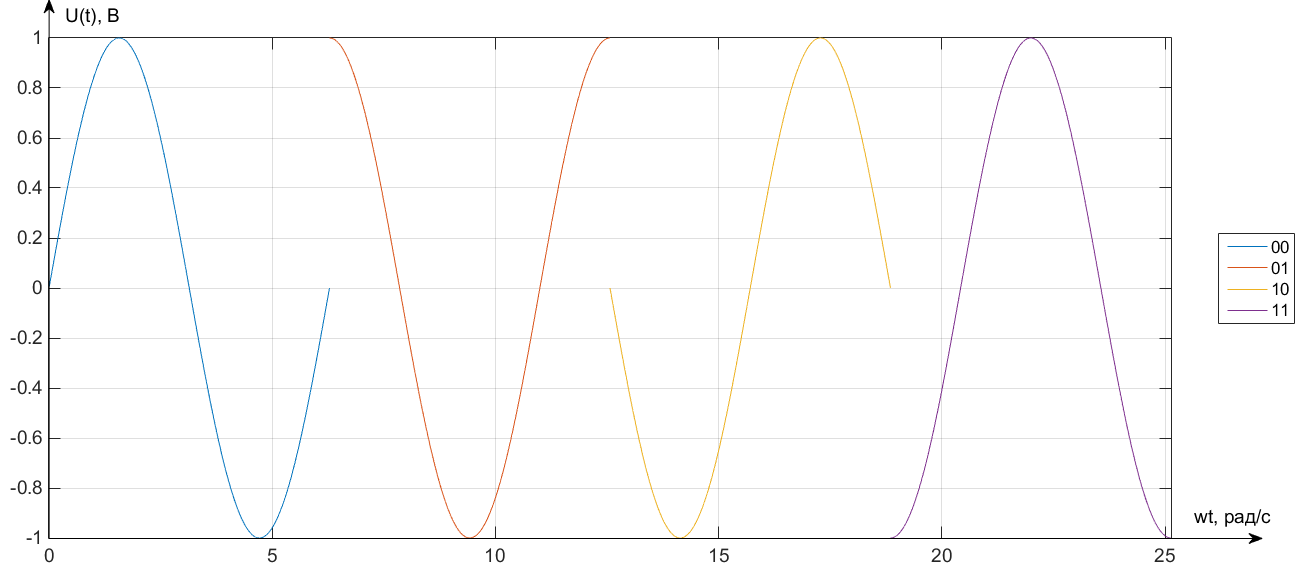
Запишем выражения, соответствующие передаче нуля и единицы с помощью двоичной фазовой модуляции. Запишем выражения, соответствующие передаче различных комбинаций из двух символов, “дебитов”, с помощью четырехпозиционной ФМ. Нарисуем временные диаграммы сигналов двоичной четырехпозиционной ФМ.
При ДФМ имеем следующие выражения:
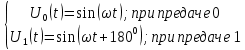
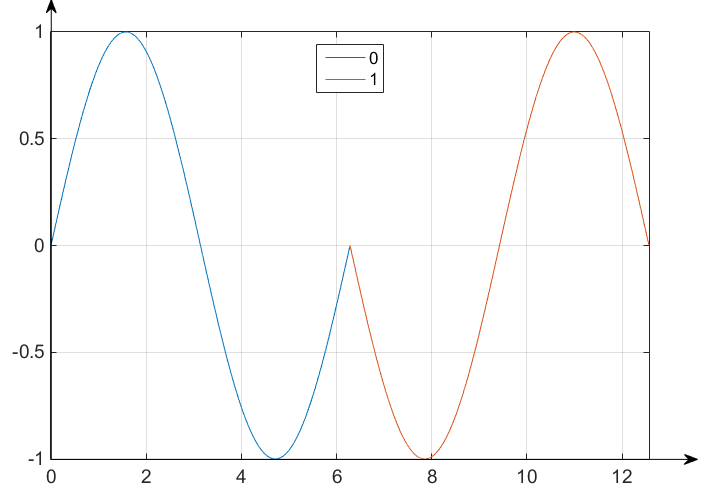
Дебиты 00, 01, 10, 11 кодируются четырёхпозиционной ФМ: