ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ ЖОҒАРҒЫ БІЛІМ МИНИСТРЛІГІ

Коммерциялық емес акционерлік қоғам «М.ӘУЕЗОВ атындағы Оңтүстік Қазақстан университеті»

«АҚПАРАТТЫҚ ТЕХНОЛОГИЯЛАР ЖӘНЕ ЭНЕРГЕТИКА» ЖОҒАРЫ МЕКТЕБІ
«ЕСЕПТЕУ ТЕХНИКАСЫ ЖӘНЕ БАҒДАРЛАМАЛЫҚ ҚАМТАМАСЫЗ ЕТУ»
кафедрасы

Зертханалық жұмыс №1
Тақырыбы: Жіктеу есептерінің сана көрсеткіштері

Орындаған: Серікбай Нұрғиса

Тобы: ИП-20-6к1

Қабылдаған: Досанова Гүлжан


Шымкент 2022ж
№ 1 зертханалық жұмыс. Жіктеу есептерінің сапа көрсеткіштері

Жұмыстың мақсаты

Бұл зертханалық жұмыстың мақсаты-екілік жіктеу сапасының негізгі көрсеткіштері және жіктеу алгоритмдерін дәл баптау нұсқалары туралы білім алу.

Қысқаша теориялық ақпарат

Жіктеу алгоритмдерінің мысалдары

Мұғаліммен Машиналық оқыту мәселесінде сапа көрсеткіштерін есептеу үшін тек екі шама қажет: нақты және болжамды мәндердің векторлары. Нақты мәндер-жаттығу және сынақ үлгісіндегі сынып белгілері; жіктеу алгоритмі болжанғандарды қайтарады.

Модельден шыққан бірнеше векторлық мысалдарды қарастырыңыз.

Біздің есепте нақты мәндер нөлдер мен бірліктердің векторын құрасын, ал болжамды мәндер интервалда болсын (мұнда сан мысалды "1"класына жатқызу ықтималдығын білдіреді). Біз мұндай векторлық жұптарды 1-суретте көрсетілгендей елестетеміз:



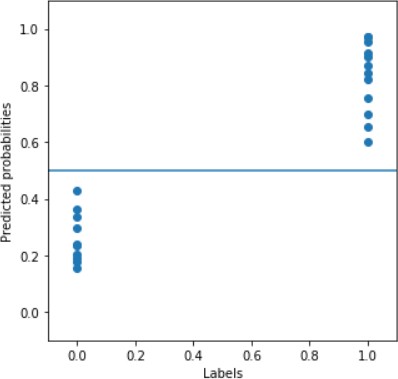
1-сурет-нақты (абсцисса осі бойынша) және болжамды (ординат осі бойынша) мәндердің мысалы

Қорытынды болжам жасау үшін (мысалды "0" немесе "1" класына жатқызу үшін) шекті (1 – суреттегі көлденең сызық) орнату керек: жоғарыда болжанған мәні бар барлық объектілерге "1" класы, қалғандарына "0"класы беріледі.

Ең жақсы жағдай: табалдырық болжамды ықтималдықтарды екі класс бойынша мүлдем дұрыс бөледі. Мысал үшін күріш. 1 ықтималдықтың идеалды аралықтарын шекті таңдау арқылы алуға болады .

---

Көбінесе ықтималдық аралықтары бір-бірінің үстіне қойылады (2б – сурет) - содан кейін шекті мұқият таңдау керек.

Қате оқытылған алгоритм керісінше орындайды: ол "0" сынып объектілерінің ықтималдығын "1" сынып мысалдарының ықтималдығынан жоғары қояды (2в сурет). Мұндай жағдайда жаттығу үлгісін алу кезінде "0" және "1" белгілерінің шатастырылғанын тексеру керек.


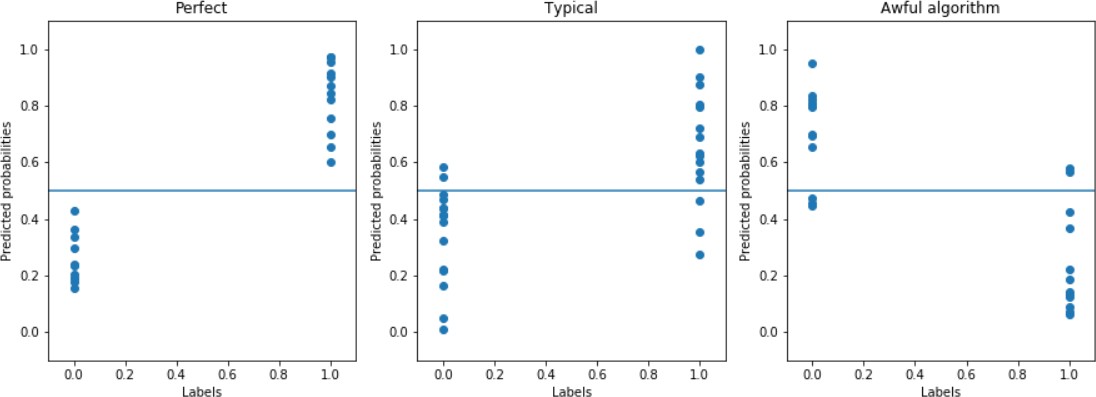
а б в

2-сурет-нақты және болжамды векторлардың мысалдары идеал (а), типтік (б) және дұрыс оқытылмаған (в) Алгоритмдер

Алгоритмдер абай болуы мүмкін және 0,5-тен тым алыс емес мәндерді шығаруы мүмкін (сурет. 3), немесе нөлге және бірлікке жақын мәндерді алу тәуекелін қабылдай алады (сурет. 4).


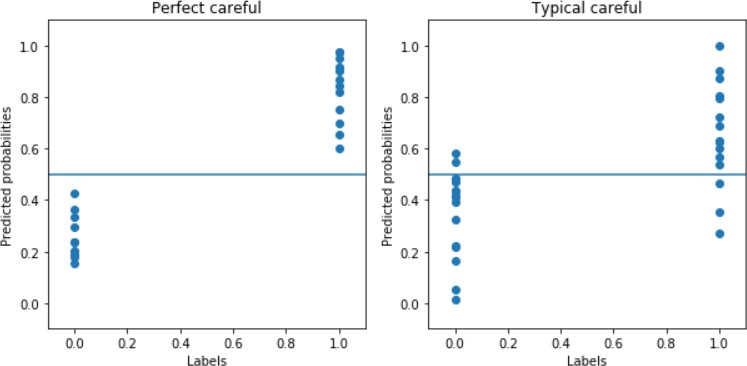
а б
3-сурет-идеалды (а) және типтік (б) сақтық алгоритмі үшін нақты және болжамды векторлардың мысалдары




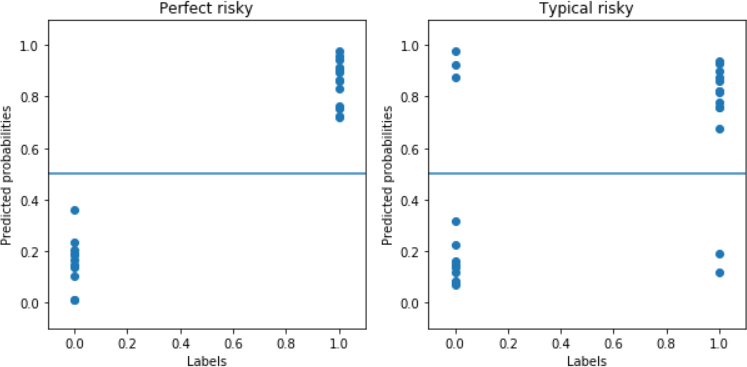
а б
4-сурет-идеалды (а) және типтік (б) тәуекел алгоритмі үшін нақты және болжамды векторлардың мысалдары

Ықтималдық аралықтарын ауыстыруға болады. Мысалы, егер I типтегі қателер қажет болмаса (false-positive), онда алгоритм орташа мәндерді нөлге жақын шығарады. Сол сияқты, II типтегі қателіктерді болдырмау үшін (false-negative) көбінесе 0,5-тен жоғары ықтималдық моделін алу қажет. 5-суретте осы жағдайлардағы векторлардың мысалдары келтірілген.


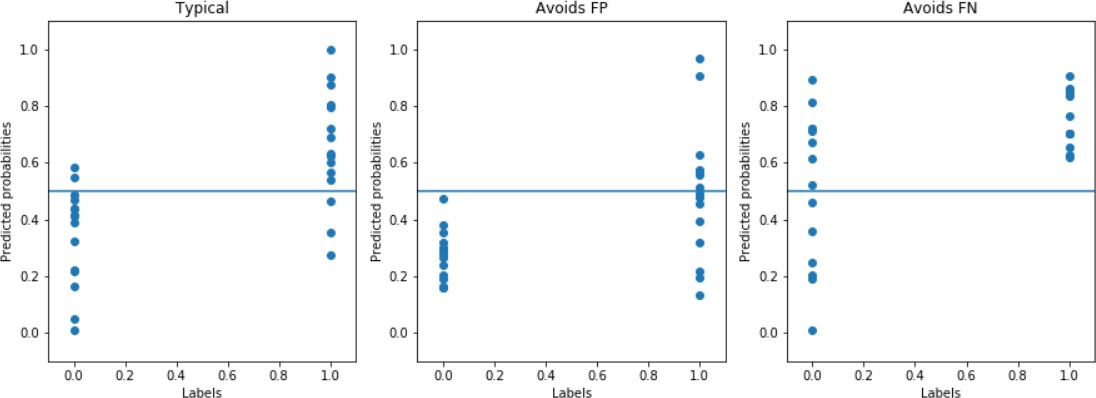
а б в
5-сурет-типтік (а) үшін нақты және болжамды векторлардың мысалдары, I тектегі қателіктерден аулақ болу (б) және II тектегі қателіктерден аулақ болу (в) Алгоритмдер

Precision және recall. Accuracy

Бұл көрсеткіштер болжанған мәндерді шекті мәнмен екілендіргеннен кейін есептеледі . 6-суретте нақты және болжамды мәндердің жұптарына байланысты объектілердің түрлері көрсетілген.



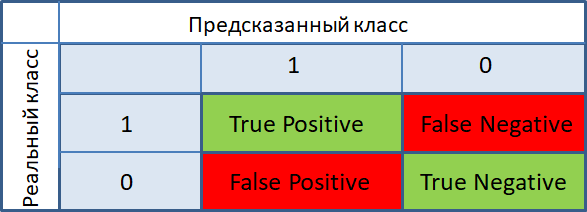
6 - сурет-нысан түрлері: True, False-сәйкесінше объектінің дұрыс және дұрыс емес болжамды класы; Positive, Negative-сәйкесінше объектінің болжамды класы "1" ("Иә") және "0" ("Жоқ")

---

Ең қарапайым және танымал метрика – accuracy. Ол дұрыс болжанған мысалдардың үлесін көрсетеді:


Барлық үш метриканың көмегімен Жақсы және нашар дайындалған жіктеу алгоритмдерінің жағдайларын оңай анықтауға болады. Сонымен қатар, мүмкін мәндер интервалда болғандықтан , оларды түсіндіру оңай.

Из данных метрик ничего нельзя узнать о самих значениях вероятностей объектов; можно определить только, какая их доля лежит не по ту сторону от порога T.

Accuracy метрикасы алгоритмге I және II қателер үшін бірдей айыппұл салады. Сонымен қатар, precision және recall жұптарын пайдалану қателер тұқымдары арасындағы қатынасты нақты орнатуға мүмкіндік береді: бұл көрсеткіштер сәйкесінше Fn және Fp қателерін бақылау үшін қолданылады.

8-суретте 5-суреттегі векторлық жұптар үшін T шекті мәніне негізделген дәлдік және қалпына келтіру көрсеткіштері берілген.

---

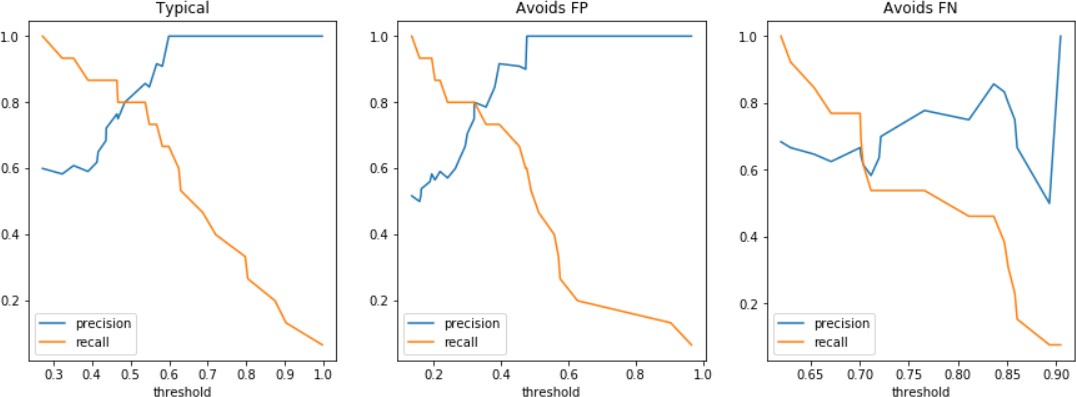
а б в

8 – сурет-precision және recall типтік үшін әр түрлі ???? шекті мәндерінде (а), i тектегі қателіктерден аулақ болу (б) және II тектегі қателіктерден аулақ болу (в) Алгоритмдер

T шекті мәні жоғарылаған сайын, қисықтардың бірі көтеріліп, екіншісі төмен қарай құлайтындығына сәйкес, біз FP-ден аз және Fn-ден көп қателіктер аламыз. Осы үлгіге сүйене отырып, precision және recall көрсеткіштері орналасқан оңтайлы шекті таңдауға болады мәндердің қолайлы аралығы. Егер мұндай шек табылмаса, оқытудың басқа алгоритмін табу керек.

Precision және recall қолайлы мәндері тапсырманың қолданбалы сипатымен анықталатынын атап өткен жөн. Мысалы, мәселе шешілген жағдайда, науқаста қарастырылып отырған ауру бар ма ("0" – дені сау," 1 " – Ауру), қателіктер өте қажет емес, сондықтан recall метрикасының мәні қойылады , . Біз пациентке оның ауру екенін айта аламыз және одан әрі диагноз қою арқылы қатені анықтай аламыз, бұл нақты ауруды елемеумен салыстырғанда әлдеқайда жақсы.

F1-score

Precision-recall жұбының айқын кемшілігі-біз екі метриканы есептейміз: алгоритмдерді салыстыру кезінде екеуін де бірден қалай пайдалану керектігі белгісіз. Бұл мәселенің шешімі метрика ????1-????????????????????:

_{????1-???????????????????? = 2} ????????????????i????i????????*???????????????????????? _.

????????????????i????i????????+????????????????????????

F1 метрика ????????????????I только I только = 1 және ???????????????????????? = 1 болғанда ғана бірлікке тең болады (яғни идеалды алгоритмде).

????1-???????????????????? көмегімен адастыру өте қиын: егер компоненттердің бірі 1-ге жақын болса, ал екіншісі төмен мәндерді көрсетсе (және мұндай жағдайды сәйкес алу оңай) сурет. 8), F1 метрика идеалды мәннен алыс болады. Бұл көрсеткішті оңтайландыру қиын, өйткені ол жоғары дәлдікті де, қателіктер арасындағы тепе-теңдікті де қажет етеді.

5А, 5б, 5в суреттерінде ұсынылған векторлар жұбы үшін ???? = кезінде 1 1-значение мәні сәйкесінше 0,828 , 0,636 және 0,765 құрады. Precision - recall жұбының бір мәні бірлікке тең болатын екінші және үшінші мысалдардың метрикалық мәндері бірінші теңдестірілген жағдаймен салыстырғанда аз болды.

Сипатталған көрсеткіштерді түсіндіру оңай, бірақ біз модельдің шығуынан алынған ақпараттың көп бөлігін ескермейміз. Кейбір тапсырмаларда Ықтималдықтар таза түрде қажет (яғни оларды екілендірусіз). Мысалы, футбол командасының ұтысына ставка қою кезінде сіз объект тағайындалатын сыныпты емес, оны тағайындау ықтималдығын білуіңіз керек. Болжамдарды екілендірмес бұрын, кез-келген заңдылықтың болуы үшін ықтималдық векторын қарастырған пайдалы болуы мүмкін.

---

Логистикалық қате функциясы (log_loss)

Метрика объектілерді белгілі бір сыныптарға жатқызу ықтималдығы мен олардың нақты сыныптары арасындағы орташа алшақтықты анықтайды:

????

1

????????????_???????????????? = − _???? ∑[????????????????????????_i * log⁽????????????????i????????????????_i⁾ + ⁽1 − ????????????????????????_i⁾ * log (1

i=1

− ????????????????i????????????????_i)],

мұндағы ???? ???? ???? ???? ???? ????i-i объектінің жарамды класы, ???? ???? ???? ???? I I I-объектіні " 1 " сыныпқа жатқызу ықтималдығы, ???? - объектілер саны. Функцияны азайту керек.

Әрі қарай, сіз бұрын қолданылған векторлық жұптар үшін қате функциясының мәнін көре аласыз.

Сапасы әртүрлі Алгоритмдер (сурет. 2):

Идеал-0,249

Типтік-0,465

Қате оқытылған – 1,527
Сақ және қауіпті Алгоритмдер (сурет. 3 және 4):

Мінсіз сақ-0,249

Идеал тәуекел-0,171

Әдеттегі сақтық-0,465

Әдеттегі тәуекел-0,614

Алгоритмдердің ???? ???? және ошиб қателіктеріне әртүрлі бейімділігі (сурет. 5):

Қателіктерден аулақ болу-0,585

Қателіктерден аулақ болу-0,589

Алдыңғы көрсеткіштер сияқты, log_loss жақсы және нашар оқытылған алгоритмдерді ажырата алады, бірақ сонымен бірге метрикалық мәндерді түсіндіру қиын: ол нөлге жете алмайды және жоғарғы жағында шектеу жоқ. Сонымен, тіпті дәл алгоритм үшін де, оның логистикалық қате функциясының мәнін қарастырсақ, оны мінсіз деп айту мүмкін болмайды.

Екінші жағынан, метрика сақ және қауіпті Алгоритмдер арасындағы айырмашылықтарды жасайды. Суреттен көрініп тұрғандай. 3Б және 4б, екілік шегі бар қате мысалдар саны ???? = 0, әдеттегі сақ және қауіпті модельдер үшін шамамен тең, ал идеалды Алгоритмдер жағдайында (сурет. 3а, 4а) қателер мүлдем жоқ. Алайда, тәуекел алгоритмі дұрыс таңдалмаған болжамдар үшін log_loss метрикасына көбірек салмақ қосады, егер модель типтік болса, сақтықпен салыстырғанда, ал егер модель мүлдем дәл болса, аз болады.

Осылайша, log_loss 0 және 1 және 0,5-ке жақын ықтималдықтарға сезімтал.

---

Смотрите также файлы

• Тема 4 Управление и организация.docx

• Программа Практическая биология.docx

• .docx

• Компьютерная сеть оао первоуральское рудоуправление.pdf

• Пример расчета основных критериев эффективности инвестиционного проекта Даны следующие условия.docx