Далее временные значения t_i, приведенные в таблице, сравниваем с Т_ср/2, поскольку нас интересует поведение системы в первый полупериод эксплуатации. Затем получим время t₀ нерабочего состояния элемента системы Х₉, выбирая лишь те случаи, когда t_i<Т_ср/2. Расчет производится по формуле



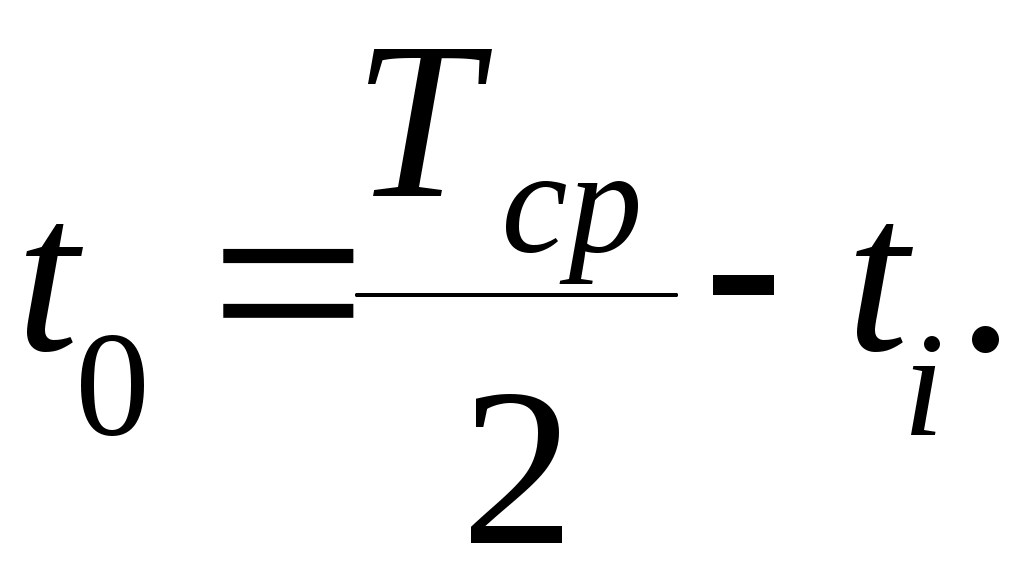
Полученное значение t₀ заносим в таблицу, указав его в скобках, затем суммируем нерабочее время в единичной реализации t₀ и берем отношение к сумме общего времени t_общ работы элемента в этой реализации. На основе полученных значений определим вероятность отказа элемента системы Х₉ для данной реализации по формуле:



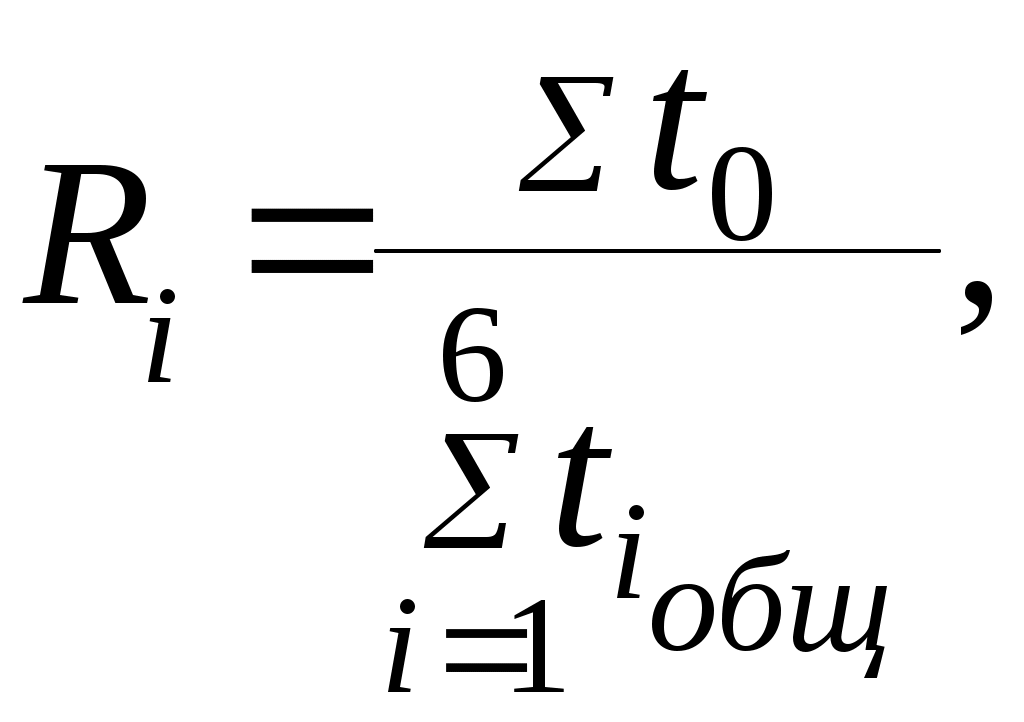
и так для каждой реализации.

Вероятность отказа элемента системы Х₃ является средним арифметическим этих значений:
R_X=1/5ΣR_i,
R_X9=
Аналогично определяем вероятности отказов элементов системы R_X4, R_x4, R_x10.
Примем среднюю наработку на отказ устройства при поломке корпуса (X₄) Т_ср = 80 000 час;

F(5000)=0,2 F(80000)=0,93

F(10000)=0,3 F(100000)=0,96

F(20000)=0,5 F( 120000)=0,98

F(40000)=0,7 F( 140000)=0,99
F(60000)=0,9




Интегральная функция экспоненциального распределения,
=1,2510^-5, 1/час.

Временная выборка из пяти реализаций для шести элементов (X₄) t10³ час

m n		Количество элементов						t0	tобщ	t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1
	2
	3
	4
	5
Итого:

---

R_X4=

Примем среднюю наработку на отказ устройства при поломке крышке (Х₇) Т_ср=80000 час.
График

Временная выборка из пяти реализаций для шести элементов (Х₇) t10³ час
Таблица
R_X7=

---

6. МОДЕЛИРОВАНИЕ ПОСТЕПЕННЫХ ОТКАЗОВ

Постепенные отказы подчиняются нормальному закону распределения. Интегральная функция нормального закона имеет вид:



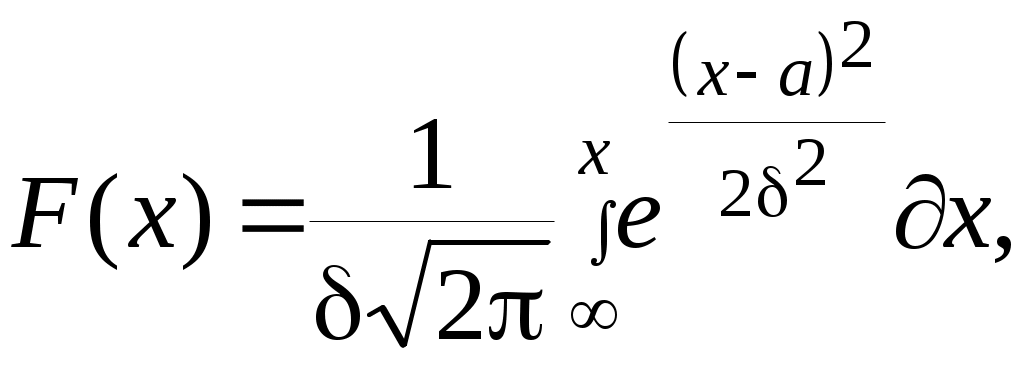
где  — среднеквадратичное отклонение;

a — математическое ожидание.

Для того чтобы не рассчитывать интеграл, воспользуемся половинной функцией Лапласа и с ее помощью рассчитаем нормальный закон распределения по формуле:



где Ф(х) — половинная функция Лапласа;
х=(t - T_ср)/, где

х — аргумент функции Лапласа;

t — время функционирования;

Т_ср — средняя наработка на отказ;

 — среднеквадратичное отклонение.

На рисунке представлен график половинной функции Лапласа.







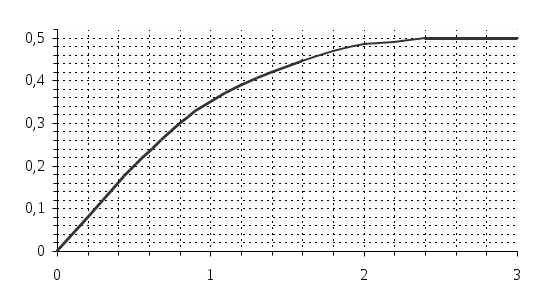
Рассчитаем интегральную функцию F(t) нормального распределения для Х₁, задавшись Т_ср= 40000 час., =500, определим аргумент функции Лапласа и занесем данные в таблицу.
Сводная таблица расчета интегральной функции
нормального распределения (Х₁)

t103, час.	18	18,5	19	19,5	20	20,5	21	21,5	22
Х	-4	-3	-2	-1	0	1	2	3	4
Ф(х)	-0,5	-0,5	-0,48	-0,34	0	0,34	0, 48	0,5	0,5
F(t)	0	0	0,02	0,16	0,5	0,84	0,98	1	1

---

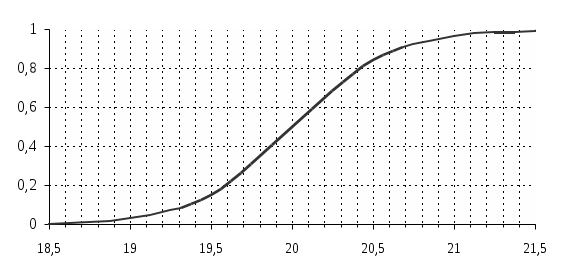
На основе расчетных данных построим график нормального распределения.

Полученную выборку 65 заносим в таблицу.

Полученные в таблице значения сравниваем с Т_ср, т. к. нас интересуют характеристики системы в первый период эксплуатации. В тех случаях, если t₀<T_ср, находим нерабочее время t₀ элемента системы Х₁по формуле . Полученное время указано в скобках в таблице. Затем, просуммировав время t₀ по реализации, берем отношение t₀ к суммарному времени функционирования элемента системы Х₁ в этой реализации . Вероятность отказа элемента системы Х₁ в данной реализации определяем по формуле:

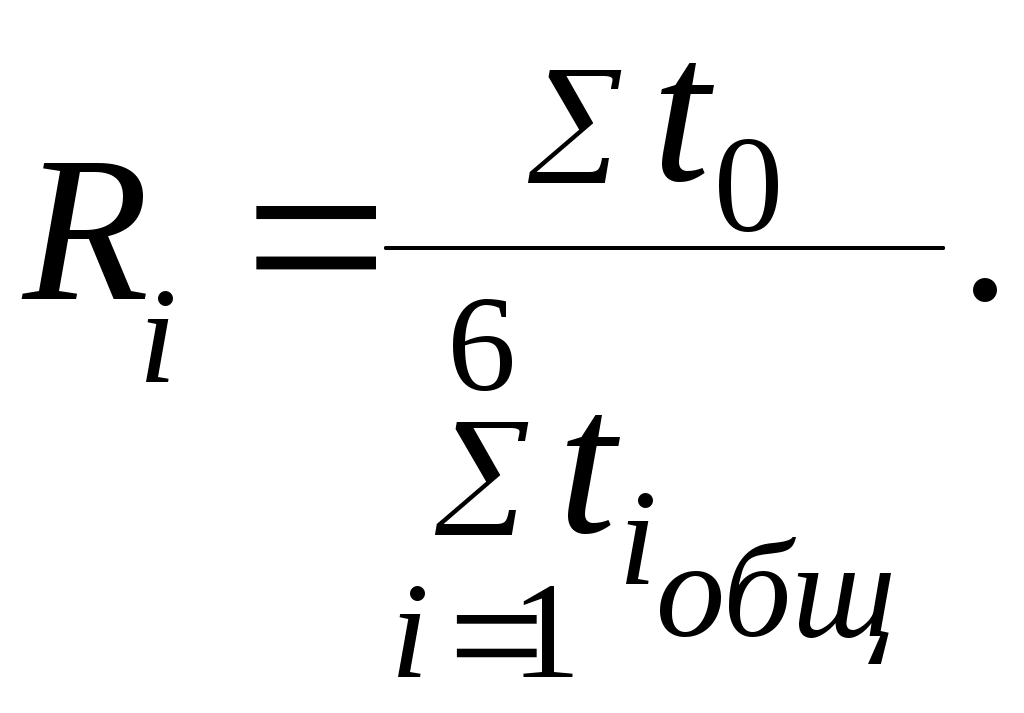
m n		Количество элементов						Σt0	tобщ	t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1
	2
	3
	4
	5
Итого:

---

R_X1=
Аналогично промоделируем для остальных элементов Х₂, Х₃, Х₄, Х₅, Х₆, Х₇, Х₈. Эти элементы системы имеют тоже самое время наработки на отказ, необходимо повторить процесс моделирования по графику.




Временная выборка из 6х5 элементов (Х₂).

m n		Количество элементов						Σt0	tобщ	t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1
	2
	3
	4
	5
Итого:

R_X2=

Временная выборка из 6х5 элементов (Х₅).

m n		Количество элементов						Σt0	tобщ	t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1
	2
	3
	4
	5
Итого:

---

Смотрите также файлы

• Лекция 18 2 часа. Способы, средства и организация пожаротушения. Прекращение процессов горения.doc

• Практическая работа по Основы экологического права дисциплине Выполнил(а) студент(ка).docx

• 1. Биологическая сущность человека 3 Смысл существования человека с философской точки зрения 4.docx

• Открытие магазина, специализирующегося на одежде для животных.docx

• Методические указания по выполнению комплексной курсовой работы по.docx