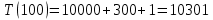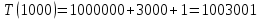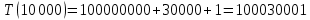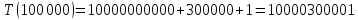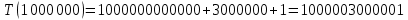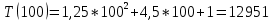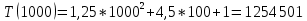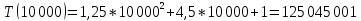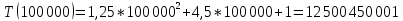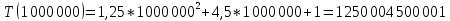Файл: Отчет по практической работе 2 Оценка сложности и определение эффективности алгоритма по дисциплине Структуры и алгоритмы обработки данных.docx
Добавлен: 11.12.2023
Просмотров: 172
Скачиваний: 18
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
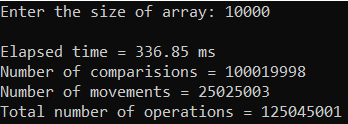
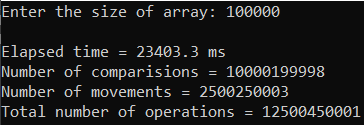
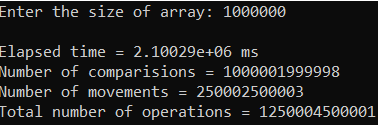
Рисунок 15 – Тестирование при n = 100.
Лучший случай
Рисунок 17 – Тестирование при n = 1000.
Лучший случай
Рисунок 23 – Тестирование при n = 1 000 000.
Лучший случай
Обработка результатов
-
Лучший случай:
Таблица 2 – Selection Sort, лучший случай
| n | T(n), мс | Тп(n) = Cф + Mф | Тт(n) = С + М |
| 100 | 0,046 | 10 301 | 10 301 |
| 1000 | 2,257 | 1 003 001 | 1 003 001 |
| 10 000 | 201,208 | 100 030 001 | 100 030 001 |
| 100 000 | 20 159,500 | 10 000 300 001 | 10 000 300 001 |
| 1 000 000 | 2 022 320,000 | 1 000 003 000 001 | 1 000 003 000 001 |
-
Худший случай:
Таблица 3 – Selection Sort, худший случай
| n | T(n), мс | Тп(n)=Cф+Mф | Тт(n)=С+М |
| 100 | 0,014 | 12 951 | 12 951 |
| 1000 | 1,146 | 1 254 501 | 1 254 501 |
| 10 000 | 115,184 | 125 045 001 | 125 045 001 |
| 100 000 | 12 382,100 | 12 500 450 001 | 12 500 450 001 |
| 1 000 000 | 1 536 200,000 | 1 250 004 500 001 | 1 250 004 500 001 |
График зависимости сложности от n
Г
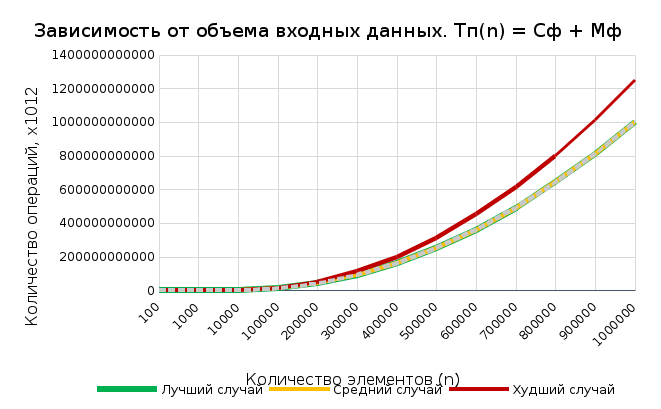 рафик 3
рафик 3Вывод по заданию 2
Полученные данные подтверждают, что сложность алгоритма имеет квадратичный характер вне зависимости от исходного состояния массива. Результаты теоретического расчета и практического выполнения совпали. В худшем случае сложность определяется формулой
 (квадратичная сложность), а в лучшем случае
(квадратичная сложность), а в лучшем случае  (квадратичная сложность).
(квадратичная сложность).Задание 3
Формулировка задания
Сравнить эффективность двух алгоритмов простых сортировок. Второй используемый алгоритм – Exchange Sort.
Описание математической модели
Осуществляется проход по массиву от 1 элемента до n-ного, сравнивая текущий элемент со всеми последующими. Если какой-то из последующих элементов меньше i-того, то меняем их местами.
Блок-схема алгоритма

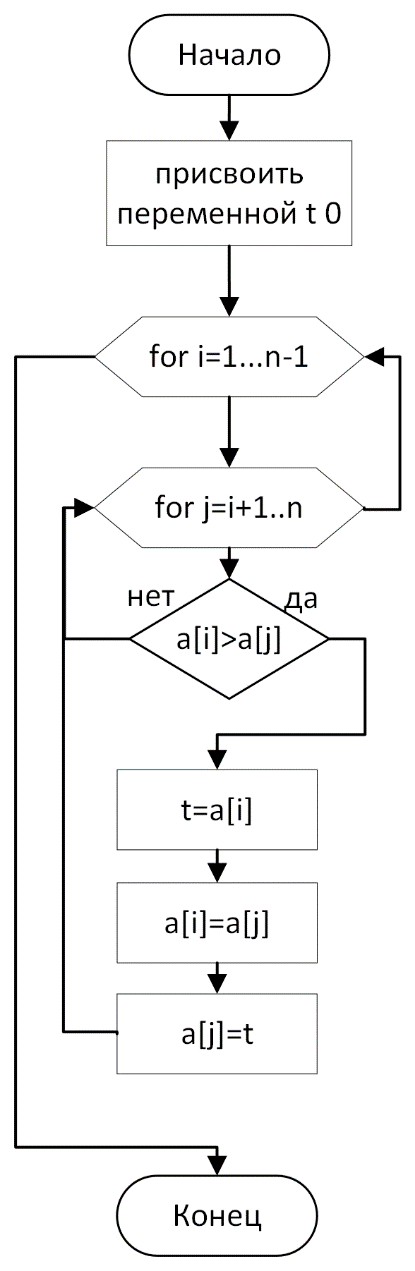
Рисунок 25 – блок-схема алгоритма сортировки
Реализация алгоритма
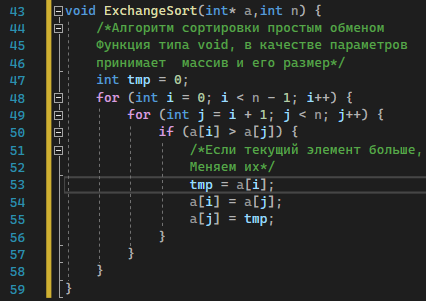

Рисунок 26 – Алгоритм сортировки
Тестирование
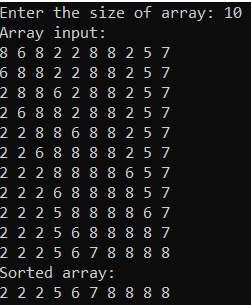


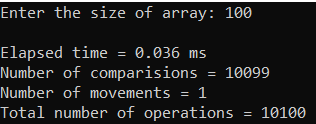
Рисунок 28 – Тестирование при n = 100. Лучший случай
Рисунок 27 – Тестирование и отладка при n = 10.
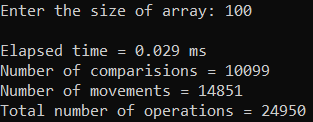





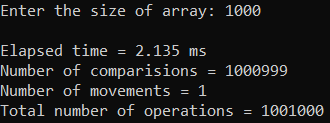
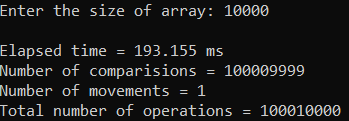
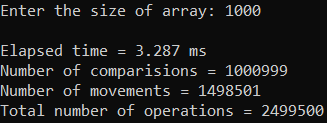
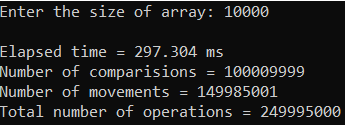
Рисунок 33 – Тестирование при n = 10 000. Худший случай
Рисунок 30 – Тестирование при n = 1000. Лучший случай
Рисунок 29 – Тестирование при n = 100. Худший случай
Рисунок 31 – Тестирование при n = 1000. Худший случай
Рисунок 32 – Тестирование при n = 10 000. Лучший случай
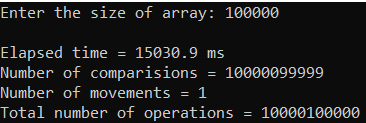

Рисунок 34 – Тестирование при n = 100 000. Лучший случай
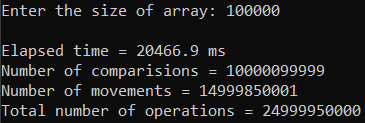

Рисунок 35 – Тестирование при n = 100 000. Худший случай
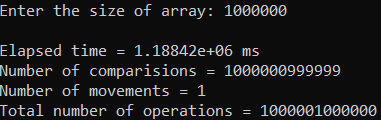


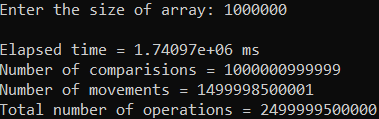
Рисунок 37 – Тестирование при n = 1 000 000. Худший случай
Рисунок 36 – Тестирование при n = 1 000 000. Лучший случай
Обработка результатов
Таблица 4 – Exchange Sort, лучший случай
| n | T(n), мс | Тп(n) = Cф + Mф |
| 100 | 0,036 | 10 100 |
| 1000 | 2,135 | 1 001 000 |
| 10 000 | 193,155 | 100 010 000 |
| 100 000 | 15 030,900 | 10 000 100 000 |
| 1 000 000 | 1 188 420,000 | 1 000 001 000 000 |
Таблица 5 – Exchange Sort, худший случай
| n | T(n), мс | Тп(n) = Cф + Mф |
| 100 | 0,029 | 24 950 |
| 1000 | 3,287 | 2 499 500 |
| 10 000 | 297,304 | 249 995 000 |
| 100 000 | 20 466,900 | 24 999 950 000 |
| 1 000 000 | 1 740 970,000 | 2 499 999 500 000 |
Оценка емкостной сложности
Используется 1 вспомогательная переменная, необходимая для перестановок. Емкостная сложность:

Графики зависимости сложности от n
Г
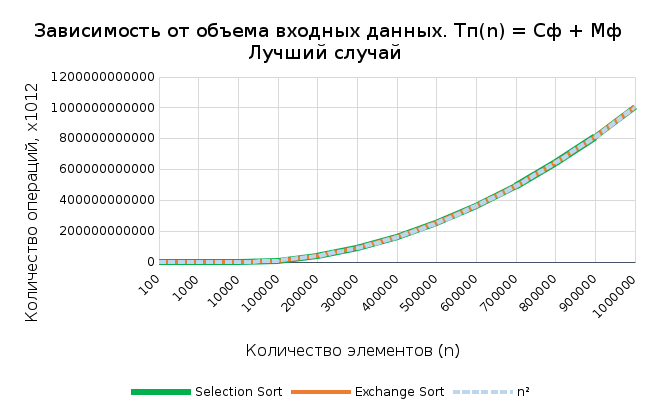 рафик 4
рафик 4Г
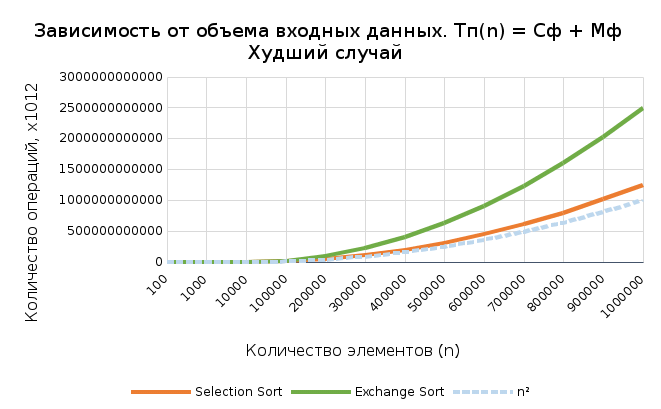 рафик 5
рафик 5Вывод по заданию 3
Полученные данные подтверждают, что оба алгоритма обладают квадратичной вычислительной сложностью, но на основе теоретического расчета можно установить, что функция роста второго алгоритма растет быстрее. Основываясь на графиках и таблицах, можно утверждать, что время выполнения зависит и от исходного состояния массива. Наибольшая разница заметна при худшем случае, в то время как сложности в лучшем и среднем случаях практически совпадают. Емкостная сложность у обоих алгоритмов – константная.
Вывод
В ходе работы приобретены и отработаны практические навыки по:
-
определению сложности алгоритмов сортировки на теоретическом и практическом уровнях; -
определению емкостной сложности алгоритмов сортировки; -
реализацией алгоритмов сортировки; -
определению зависимости (квадратичной/линейной) сложности алгоритма сортировки от объема входных данных; -
нахождению оптимального алгоритма сортировки с помощью данных, полученных в ходе теоретического расчета и практического выполнения.