Файл: Отчет по практической работе 2 Оценка сложности и определение эффективности алгоритма по дисциплине Структуры и алгоритмы обработки данных.docx

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«МИРЭА – Российский технологический университет»

РТУ МИРЭА


ОТЧЕТ

ПО ПРАКТИЧЕСКОЙ РАБОТЕ №2

Оценка сложности и определение эффективности алгоритма

по дисциплине

«Структуры и алгоритмы обработки данных»

Выполнил студент группы	ИКБО-27-22

Практическая работа выполнена	«__» марта 2023 г.	Ломилин М. Ю.
		(подпись студента)
«Зачтено»	«__» _________2023 г.	Ермаков С.Р.
		(подпись руководителя)

Москва 2023
Содержание

Цель работы

Приобретение практических навыков, связанных с:

• 
  определением сложности алгоритмов эмпирическим способом;
  
• 
  реализацией алгоритмов сортировки;
  
• 
  нахождением эффективного алгоритма решения задачи из нескольких
  

определением емкостной и временной сложностей алгоритма и их зависимости от объема входных данных.

• 
  
  

Ход работы

Задание 1

Формулировка задания

Оценить эффективность простого алгоритма сортировки на массиве, заполненном случайными числами (в среднем случае). Используемый алгоритм – Selection Sort.

---

Описание математической модели

Идет проход по массиву с помощью цикла для i. В min записывается значение текущего индекса. С помощью внутреннего цикла происходит поиск минимума и перезапись min. После выполнения внутреннего цикла при неравенстве текущего индекса и min происходит перестановка элементов.

Блок-схема алгоритма

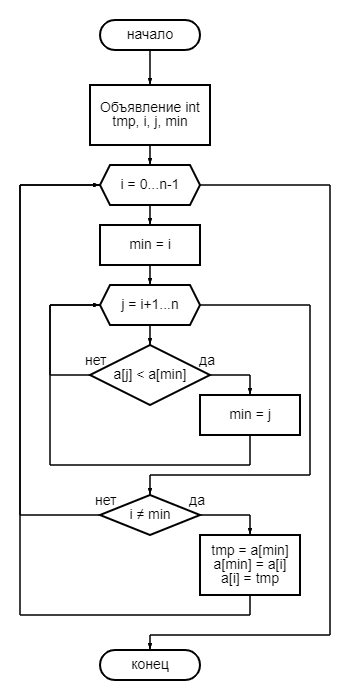
Рисунок 1 – блок-схема алгоритма сортировки

Код программы

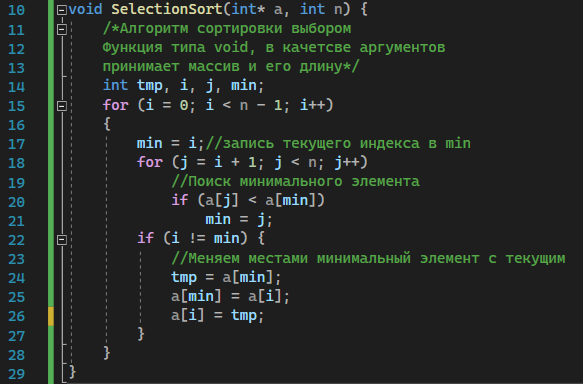
Рисунок 2 – Алгоритм сортировки

Рисунок 3 – Функция вывода массива

Рисунок 4 – Функция заполнения массива случайными числами





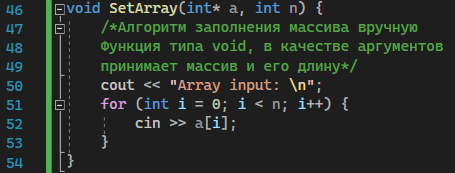
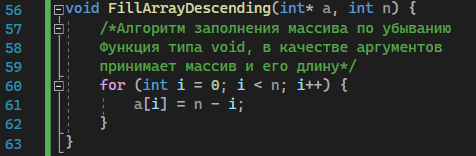
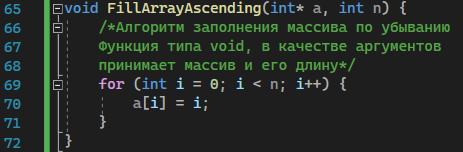
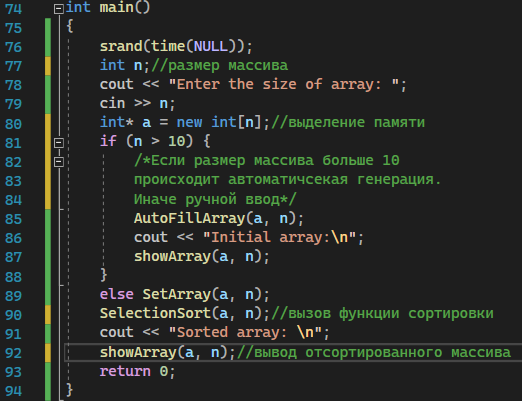
Рисунок 8 – Функция main

Рисунок 6 – Функция заполнения массива числами по убыванию

Рисунок 5 – Функция ручного заполнения массива

Рисунок 7 – Функция заполнения массива числами по возрастанию

---

Тестирование

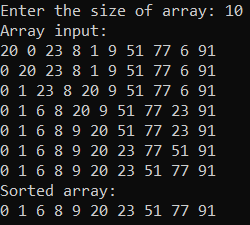
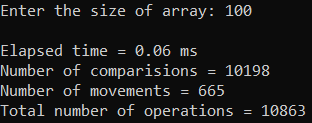
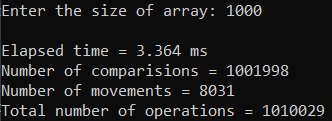
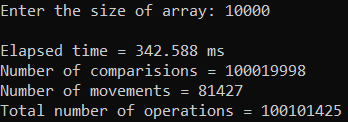
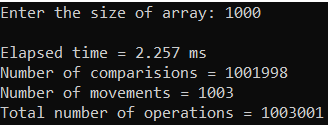
Рисунок 10 – Тестирование при n = 100. Средний случай

Рисунок 9 – Тестирование и отладка при n = 10.

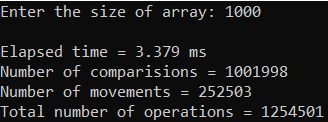
Рисунок 11 – Тестирование при n = 1000. Средний случай

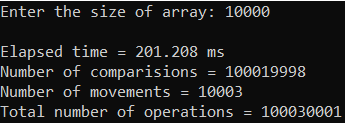
Рисунок 12 – Тестирование при n = 10 000. Средний случай





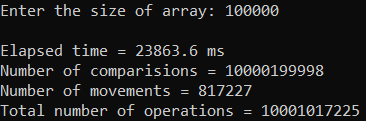
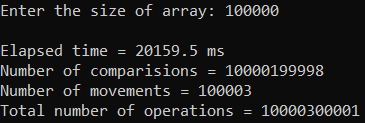
Рисунок 13 – Тестирование при n = 100 000. Средний случай





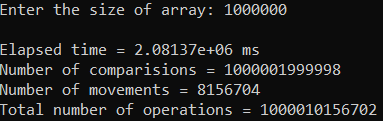
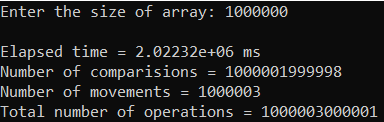
Рисунок 14 – Тестирование при n = 1 000 000. Средний случай

Обработка результатов

Таблица 1 – Selection Sort, средний случай

n	T(n), мс	Тп(n) = Cф + Mф
100	0,060	10 863
1000	3,364	1 010 029
10 000	342,588	100 101 425
100 000	23 863,600	10 001 017 225
1 000 000	2 081 370,000	1 000 010 156 702

Оценка емкостной сложности

Используется 1 вспомогательная переменная, необходимая для перестановок. Емкостная сложность:

---

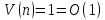
Графики зависимости сложности от n

Г 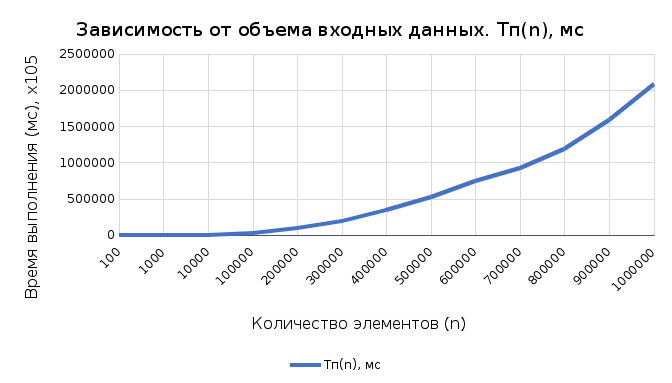рафик 1

Г 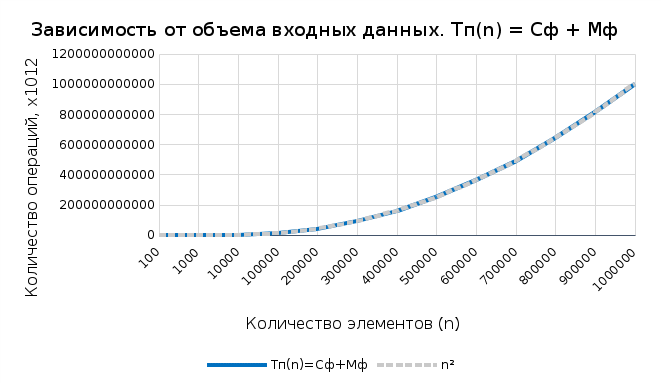рафик 2

Вывод по заданию 1

На основании данных, полученных в ходе работы, можно сделать следующий вывод: алгоритм обладает квадратичной вычислительной сложностью, что является показателем низкой эффективности, а также имеет константную емкостную сложность, что для внутренней сортировки приемлемо.

Задание 2

Формулировка задания

Оценить эффективность алгоритма простой сортировки в случай строгой упорядоченности по возрастанию и убыванию (условно лучший и худший случаи). Используемый алгоритм – Selection Sort.

Вычислительная сложность алгоритма

Номер оператора	Оператор	Кол-во выполнений оператора в строке
1	SelectionSort(int* a, int n) {
2	int tmp, i, j, min;	4
3	for (i = 1; i <= n-1; i++) do	n
4	min = i	n-1
5	for (j=i+1; j<=n; j++) do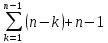
6	if (a[j] < a[min]) then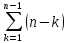
7	min = j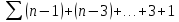
8	endif
9	od
10	if (i != min) then	n-1
11	tmp = a[min]	n/2
12	a[min] = a[i]	n/2
13	a[i] = tmp	n/2
14	endif
15	od
16	}

---

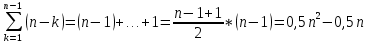
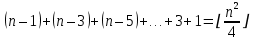
Общая вычислительная сложность алгоритма:

• 
  В лучшем случае (массив отсортирован в возрастающем порядке):
  

• 
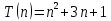
  В худшем случае (массив отсортирован в убывающем порядке):
  

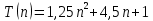
Т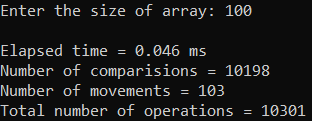 естирование

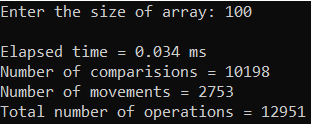
Рисунок 16 – Тестирование при n = 100.

Худший случай

Рисунок 24 – Тестирование при n = 1 000 000.

Худший случай

Рисунок 22 – Тестирование при n = 100 000.

Худший случай

Рисунок 18 – Тестирование при n = 1000.

Худший случай

Рисунок 20 – Тестирование при n = 10 000.

Худший случай

Рисунок 19 – Тестирование при n = 10 000.

Лучший случай

Рисунок 21 – Тестирование при n = 100 000.

Лучший случай

---