ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 110
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Алгоритмопределения достоверности совпадений и различий для экспериментальных данных, из- меренных в порядковой шкале, заключается в следующем:
-
Вычислить для сравниваемых выборок
(5).
2
c
эмп
-
эмпирическое значение критерия 2 по формуле
-
Сравнить это значение с критическим значением
2
c
0.05
, взятым из таблицы 9: если
2
c
эмп
2
c
,
0.05
то сделать вывод: "характеристик сравниваемых выборок совпадают с уровнем значимости
0,05"; если
2
c
>
эмп
2
c
0.05
, то сделать вывод "достоверность различий характеристик сравниваемых
выборок составляет 95%".
Применим алгоритм для данных из таблицы 4. Сначала вычисляем по формуле (5) эмпирические значения критерия 2. Для примера приведем расчет. Параметры экспериментальной группы (N = 25) после окончания эксперимента: n1 = 2, n2 = 13, n3 = 10 (то есть 2 учащихся продемонстрировали "низ- кий" уровень знаний, 13 – "средний" и 10 – "высокий" – см. выше таблицу 4), контрольной группы (M= 30): m1= 12,m2= 10, m3=8. Подставляя в формулу (5), получаем:
c
2
эмп
= 2530[( 2 –12 )2 / (2 + 12) + ( 13 –10 )2 / (13 + 10) + ( 10 –8 )2 / (10 + 8)] = 7,36.
25 30
25 30
25 30
Аналогичным образом вычисляются все оставшиеся из 16 возможных результатов парных сравне- ний групп (экспериментальная и контрольная группы, до начала и после окончания эксперимента). Результаты вычислений приведены в таблице 10. Ячейки таблицы 10 содержат эмпирические значения критерия 2 для сравниваемых групп, соответствующих строке и столбцу. Жирным шрифтом выделены результаты сравнения характеристик экспериментальной и контрольной группы до начала и после окончания эксперимента. Например, эмпирическое значение критерия 2, получаемое при сравнении характеристик контрольной группы до начала эксперимента (вторая строка таблицы 10) и эксперимен- тальной группы до начала эксперимента (третий столбец таблицы 10), равно 0,03.
В рассматриваемом примере L=3(выделены три уровня знаний – "низкий", "средний" и
"высокий"). Следовательно, L–1=2. Из таблицы 9 получаем для L– 1 = 2:
2
c
0.05
= 5,99. Тогда из табли-
цы 10 видно, что все эмпирические значения критерия 2, кроме результата cэмп=7,36 сравнения экспе- риментальной и контрольной групп после окончания эксперимента, меньше критического значения.
Следовательно "характеристики всех сравниваемых выборок, кроме экспериментальной и кон- трольной групп после окончания эксперимента, совпадают33 с уровнем значимости 0,05".
0.05
Так как cэмп =7,36 > 5,99 = c2
, то "достоверность различий характеристик экспериментальной и
контрольной групп после окончания эксперимента составляет 95%".
32 Критерий хи-квадрат применим при условии, что для любого значения балла в любой из сравниваемых выборок не менеепятиеечленовполучилиданныйбалл,тоесть:ni5,mi5,i= 1,2,…,L.Крометого,желательно,чтобычислоградацийL было не менее трех. Если L = 2, то есть используется дихотомическая шкала ("да" – "нет", "решил" – "не решил" и т.д.),то можноприменятькритерийФишера–см.ниже.
33 Интересноотметить, чтохарактеристикиэкспериментальнойгруппыдоначалаипослеокончанияэкспериментатакжесовпадаютс уровнемзначимости0,05.
Итак, начальные (до начала эксперимента) состояния экспериментальной и контрольной групп сов- падают, а конечные (после окончания эксперимента) – различаются. Следовательно, можно сделать вывод, что эффект изменений обусловлен именно применением экспериментальной методики обучения.
Эмпирические значения критерия 2 для данных из таблицы 4
Таблица10
| | Контрольная группа до начала экспе- римента | Эксперимен- тальная группа до начала экспе- римента | Контрольная группа после окончания эксперимента | Эксперимен- тальная группа после окончания эксперимента |
| Контрольная группа до начала экспери- мента | 0 | 0,03 | 1,16 | 4,60 |
| Экспериментальная группа до начала эксперимента | 0,03 | 0 | 1,34 | 3,82 |
| Контрольная группа после окончания эксперимента | 1,16 | 1,34 | 0 | 7,36 |
| Экспериментальная группа после окон- чания эксперимента | 4,60 | 3,82 | 7,36 | 0 |
Дихотомическая шкала. Отдельно рассмотрим случай, когда используется дихотомическая шкала
-
порядковая шкала с всего двумя различными упорядоченными баллами – "высокий"-"низкий", "спра- вился с заданием"-"не справился", "прошел тест"-"не прошел" и т.д. Характеристикой группы, помимо общего числа ее членов, будет число членов (или доля, процент от общего числа), набравших заданный, например – максимальный, балл (в общем случае – число членов, обладающих заданным признаком).
Для экспериментальной группы, описываемой двумя числами (n1, n2), где n1– число членов рас- сматриваемой группы, набравших низкий балл, n2– набравших высокий балл, n1 + n2 = N, доля p ее членов, набравших максимальный балл, равна: p = n2 / N. Для контрольной группы, описываемой двумя числами (m1,m2), где m1+m2 =M, доля qее членов, набравших максимальный балл, равна: q= m2 /M.
Рассмотрим пример: для каждого из столбцов таблицы 1, считая, что возможны два уровня знаний – "не усвоили материал" (число правильно решенных задач меньше либо равно 10) и "успешно усвоили материал" (число правильно решенных задач строго больше 10) определяем распределение членов экспериментальной и контрольной группы по двум уровням знаний и получаем таблицу 11 (для экспе- риментальной группы до начала эксперимента p = 0,72 (или 72%), после окончания эксперимента p=0,92; для контрольной группы до начала эксперимента q=0,70, после окончания эксперимента q =0,60).
Таблица11
Результаты дихотомических измерений уровня знаний
в контрольной и экспериментальной группах до и после эксперимента
| | Контроль- ная группа до начала экспери- мента | Экспери- ментальная группа до начала экспери- мента | Контроль- ная группа после окон- чания экс- перимента | Экспери- ментальная группа после окон- чания экс- перимента |
| Доля, которую составляют учащиеся, не усвоившие материал | 0,30 | 0,28 | 0,40 | 0,08 |
| Доля, которую составляют учащиеся, усвоившие ма- териал | 0,70 | 0,72 | 0,60 | 0,92 |
Для данных, измеренных в дихотомической шкале целесообразно использование критерия Фише-ра34, для которого эмпирическое значение j эмпвычисляется по следующей формуле (арксинус может быть вычислен в Excel):
-
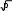
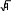
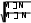jэмп= |2 arcsin( ) – 2 arcsin( )| .
Критическое значение j0.05критерия Фишера для уровня значимости 0,05 равно 1,64.
Алгоритм определения достоверности совпадений и различий для экспериментальных данных, из- меренных в дихотомической шкале, заключается в следующем:
-
Вычислить для сравниваемых выборок j эмп– эмпирическое значение критерия Фишера по фор- муле (6). -
Сравнить это значение с критическим значением j 0.05= 1,64: если j эмп1,64, то сделать вывод: "характеристики сравниваемых выборок совпадают с уровнем значимости 0,05"; если j эмп > 1,64, то сделать вывод "достоверность различий характеристик сравниваемых выборок составляет 95%".
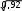
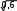
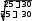Применим алгоритм для экспериментальных данных из таблицы 11. Сначала вычисляем по форму- ле (2) эмпирические значения критерия Фишера. Для примера приведем расчет. Параметры экспери- ментальной группы (N=25) после окончания эксперимента: p=0,92, контрольной группы (M= 30): q=0,60 (см. таблицу 11). Подставляя в формулу (6), получаем:jэмп=|2arcsin(
) – 2 arcsin( )|
=2,94.
Аналогичным образом вычисляются все оставшиеся из 16 возможных результатов парных сравне- ний групп (экспериментальная и контрольная группы, до начала и после окончания эксперимента). Результаты вычислений приведены в таблице 12. Ячейки таблицы 12 содержат эмпирические значения критерия Фишера для сравниваемых групп, соответствующих строке и столбцу. Жирным шрифтом выделены результаты сравнения характеристик экспериментальной и контрольной группы до начала и после окончания эксперимента.
Например, эмпирическое значение критерия Фишера, получаемое при сравнении характеристик контрольной группы до начала эксперимента (вторая строка таблицы 12) и экспериментальной группы до начала эксперимента (третий столбец таблицы 12), равно 0,16. Следовательно "состояния экспери- ментальной и контрольной групп до начала эксперимента совпадают с уровнем значимости 0,05".
Теперь аналогичным образом сравним характеристики экспериментальной и контрольной групп по- сле окончания эксперимента. Так как j эмп = 2,94 > 1,64 = j кр, то "достоверность различий состояний экспериментальной и контрольной групп после окончания эксперимента составляет 95%".
Таблица12
Эмпирические значения критерия Фишера для данных из таблицы 11
| | Контроль- ная группа до начала эксперимен- та | Экспери- ментальная группа до начала экс- перимента | Контроль- ная группа после окон- чания экспе- римента | Экспери- ментальная группа после окончания эксперимен- та |
| Контрольная группа до начала эксперимента | 0 | 0,16 | 0,81 | 2,16 |
| Экспериментальная группа до начала экс- перимента | 0,16 | 0 | 0,94 | 1,92 |
| Контрольная группа после окончания экс- перимента | 0,81 | 0,94 | 0 | 2,94 |
| Экспериментальная группа после оконча- ния эксперимента | 2,16 | 1,92 | 2,94 | 0 |
34ВматематическойстатистикесуществуетнесколькокритериевФишера. Мыиспользуемодиниз них–такназываемоеугловоепреобразование,поэтому далееподкритерием ФишерабудемпониматьименноугловоепреобразованиеФишера.