ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 108
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Критерий Вилкоксона-Манна-Уитни29. Данный критерий оперирует не с абсолютными значе- ниями элементов двух выборок, а с результатами их парных сравнений. Например, существенно, что учащийся Петров решил больше задач, чем учащийся Иванов, а на сколько больше – не важно.
Возьмем две выборки30: {xi}i=1…Nи {yj}j=1…Mи для каждого элемента первой31 выборки xi, i=1…N,
определим число aiэлементов второй выборки, которые превосходят его по своему значению (то есть
24 Критерий Крамера-Уэлча является более эффективным "заменителем" такого известного в физике и технике критериякакt-критерий(критерийСтьюдента).
25 Критерий Вилкоксона-Манна-Уитни плохо применим в условиях, когда число отличающихся друг от друга значений ввыборкахмало.
26 Две выборки могут иметь одинаковые средние (то есть, критерий Крамера-Уэлча установит совпадение средних), норазличаться, например, разбросом. Те различия, которые не выявит критерий Крамера-Уэлча, могут быть выявлены кри-териемВилкоксона-Манна-Уитни.
27 Корректнее говорить, что достоверность различий составляет не менее 95%, однако, так мы условились считатьдостаточной95%-уюдостоверностьразличий, тобудемговорить, чтодостоверностьразличийсоставляет95%.
28 Для сокращения ручных расчетов средние и дисперсии могут быть вычислены в рамках описательной статистики в
компьютернойпрограммеMicrosoftExcelдля Windows –см.выше таблицу6.
29 Существуют два критерия – Вилкоксона и Манна-Уитни, однако, так как они однозначно связаны между собой, будемговоритьободномкритерииВилкоксона-Манна-Уитни.
число таких yj, что yj>xi), а также число biэлементов второй выборки, которые по своему значению равны ему (то есть число таких yj, что yj=xi). Сумма
2
N
a+ a+ …+a+1 (b+ b+…+b) = +1 N
1 2 N 2 1 2
Nai
i1
bi
i1
по всем Nчленам первой выборки называется эмпирическимзначениемкритерияМанна-Уитнии обо- значается U.
Определим эмпирическоезначениекритерияВилкоксона:
| NM U|
-
Wэмп =2 .
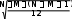
Алгоритм определения достоверности совпадений и различий для экспериментальных данных, из- меренных в шкале отношений, с помощью критерия Вилкоксона-Манна-Уитни заключается в следую- щем:
-
Вычислить для сравниваемых выборок Wэмп– эмпирическое значение критерия Вилкоксона по формуле (4). -
Сравнить это значение с критическим значением W0.05 = 1,96: если Wэмп1,96, то сделать вывод: "характеристики сравниваемых выборок совпадают с уровнем значимости 0,05"; если Wэмп > 1,96, то сделать вывод "достоверность различий характеристик сравниваемых выборок составляет 95%".
В качестве примера применим алгоритм для данных из таблицы 1.
Для этого сравним сначала числа правильно решенных задач в контрольной и экспериментальной группе до начала эксперимента. В таблице 8 приведены результаты экспериментальной группы (второй столбец), и контрольной группы (пятый столбец), а также для каждого члена экспериментальной груп- пы подсчитано число членов контрольной группы, решивших строго большее (чем он) число задач, плюс полусумма числа членов контрольной группы, решивших такое же (что и он) число задач (третий столбец). Например, в таблице 8 серым цветом в пятом столбце помечены члены контрольной группы, правильно решившие строго большее число задач, чем первый член (то есть i = 1) экспериментальной группы, который правильно решил 12 задач. Значит x1 = 12 и число таких yj, что yj > x1равно 16. Следо- вательно, a1 = 16. Число таких yj, что yj = x1равно 2. Следовательно, b1 = 2. Итак, a1 + b1 / 2 = 17, то есть число затененных ячеек равно 17. Записываем это число во вторую строку третьего столбца. Аналогич- но заполняются остальные строки третьего столбца.
Таблица8
Пример вычисления эмпирического значения критерия Манна-Уитни
| Номер члена эксперименталь- ной группы i | Число задач, правильно ре- шенных i-ым членом экспери- ментальной группы до начала эксперимента xi | Число членов контрольной группы, пра- вильно решив- ших строго большее число задач, чем i-ый член эксперимен- тальной группы ai + b i/ 2 | Номер члена контрольной группы j | Число задач, правильно ре- шенных j-ым членом кон- трольной группы до начала экспе- римента yj |
| 1 | 12 | 17 | 1 | 15 |
| 2 | 11 | 19,5 | 2 | 13 |
| 3 | 15 | 9 | 3 | 11 |
| 4 | 17 | 5 | 4 | 18 |
| 5 | 18 | 4 | 5 | 10 |
| 6 | 6 | 28,5 | 6 | 8 |
| 7 | 8 | 24,5 | 7 | 20 |
30ОграничениенаиспользованиекритерияВилкоксона-Манна-Уитниследующее:каждаявыборкадолжнасодержатьнеменеетрех элементов,еслижеводнойизвыбороквсегодваэлемента, тововторойихдолжнобыть неменеепяти.
31Какуювыборкусчитатьпервой,акакуювторой,неимеетзначения,хотяпривычисленияхудобнеепервойсчитатьтувыборку, в которойменьшечленов.
| Номер члена эксперименталь- ной группы i | Число задач, правильно ре- шенных i-ым членом экспери- ментальной группы до начала эксперимента xi | Число членов контрольной группы, пра- вильно решив- ших строго большее число задач, чем i-ый член эксперимен- тальной группы ai + b i/ 2 | Номер члена контрольной группы j | Число задач, правильно ре- шенных j-ым членом кон- трольной группы до начала экспе- римента yj |
| 8 | 10 | 21,5 | 8 | 7 |
| 9 | 16 | 6 | 9 | 8 |
| 10 | 12 | 17 | 10 | 12 |
| 11 | 15 | 9 | 11 | 15 |
| 12 | 14 | 12 | 12 | 16 |
| 13 | 19 | 2 | 13 | 13 |
| 14 | 13 | 14,5 | 14 | 14 |
| 15 | 19 | 2 | 15 | 14 |
| 16 | 12 | 17 | 16 | 19 |
| 17 | 11 | 19,5 | 17 | 7 |
| 18 | 16 | 6 | 18 | 8 |
| 19 | 12 | 17 | 19 | 11 |
| 20 | 8 | 24,5 | 20 | 12 |
| 21 | 13 | 14,5 | 21 | 15 |
| 22 | 7 | 27 | 22 | 16 |
| 23 | 15 | 9 | 23 | 13 |
| 24 | 8 | 24,5 | 24 | 5 |
| 25 | 9 | 22,5 | 25 | 11 |
| – | – | | 26 | 19 |
| – | – | | 27 | 18 |
| – | – | | 28 | 9 |
| – | – | | 29 | 6 |
| – | – | | 30 | 15 |
Сумма всех 25 чисел в третьем столбце таблицы 8 дает эмпирическое значение критерия Манна- Уитни U = 373. Вычисляем по формуле (4) значение Wэмп= 0,0338 1,96. Следовательно, гипотеза о том, что сравниваемые выборки совпадают, принимается на уровне значимости 0,05.
Теперь аналогичным образом (построив таблицу, аналогичную таблице 8, и вычислив эмпирическое значение критерия Вилкоксона) сравним числа правильно решенных задач в контрольной и экспери- ментальной группе после окончания эксперимента. Вычисляем по формуле (4) значение Wэмп= 2,1974 > 1,96. Следовательно, достоверность различий сравниваемых выборок составляет 95%.
Итак, начальные (до начала эксперимента) состояния экспериментальной и контрольной групп сов- падают, а конечные (после окончания эксперимента) – различаются. Следовательно, можно сделать вывод, что эффект изменений обусловлен именно применением экспериментальной методики обучения. Методикаопределениядостоверностисовпаденийиразличийдляэкспериментальныхдан- ных,измеренныхвпорядковойшкале. Рассмотрим случай, когда используется порядковая шкала с Lразличными баллами. Характеристикой группы будет число ее членов, набравших тот или иной балл. Для экспериментальной группы вектор баллов есть n=(n1,n2,…,nL), где nk– число членов эксперимен- тальной группы, получивших k-ый балл, k=1,2,…,L. Для контрольной группы
вектор баллов есть m=(m1,m2,…, mL), где mk– число членов контрольной группы, получивших k-ый балл, k=1,2,…,L.
Для рассматриваемого нами числового примера (L=3 – "низкий", "средний" или "высокий" уровень знаний) данные приведены в таблице 4.
Для данных, измеренных в порядковой шкале (см., например, таблицу 4), целесообразно использо- вание критерияоднородности2 ("хи" – буква греческого алфавита, название критерия читается: "хи-
квадрат"), эмпирическое значение та приведен ниже):
2
c
эмп
которого вычисляется по следующей формуле32 (пример расче-
(
L
ni mi)2
-
c2
=N M N M .
эмп
i1 ni mi
Критические значения
2
c
0.05
критерия 2 для уровня значимости 0,05 приведены в таблице 9 (стати-
стические таблицы критических значений статистических критериев для различных уровней значимо- сти и различных – в том числе больших 10 – градаций шкалы отношений можно найти, практически, в любом учебнике по статистическим методам или в специальных статистических таблицах).
Критические значения критерия 2 для уровня значимости a=0.05
Таблица9
| L–1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| c2 0.05 | 3,84 | 5,99 | 7,82 | 9,49 | 11,07 | 12,59 | 14,07 | 15,52 | 16,92 |