ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 113
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, перейдем к общей методике опреде- ления степени достоверности совпадений и различий, а затем опишем ее применение сначала для дан- ных, измеренных в шкале отношений, а затем – для данных, измеренных в порядковой шкале.
Общие подходы к определению достоверности совпадений и различий. Как отмечалось выше, типовой задачей анализа данных в педагогических исследованиях является установление совпадений или различий характеристик экспериментальной и контрольной группы. Для этого формулируются статистическиегипотезы:
Для принятия решений о том, какую из гипотез (нулевую или альтернативную) следует принять, используют решающие правила – статистические критерии23. То есть, на основании информации о результатах наблюдений (характеристиках членов экспериментальной и контрольной группы) вычисля- ется число, называемое эмпирическим значением критерия. Это число сравнивается с известным (на- пример, заданным таблично) эталонным числом, называемым критическимзначением критерия.
Критические значения приводятся, как правило, для нескольких уровней значимости. Уровнем зна- чимости называется вероятность ошибки, заключающейся в отклонении (не принятии) нулевой гипоте- зы, то есть вероятность того, что различия сочтены существенными, а они на самом деле случайны. Обычно используют уровни значимости (обозначаемые a ), равные 0,05, 0,01 и 0,001. В педагогических исследованиях обычно ограничиваются значением 0,05, то есть, грубо говоря, допускается не более чем 5% возможность ошибки.
Если полученное исследователем эмпирическое значение критерия оказывается меньше или равно
критическому, то принимается нулевая гипотеза – считается, что на заданном уровне значимости (то есть при том значении a , для которого рассчитано критическое значение критерия) характеристики экспериментальной и контрольной групп совпадают. В противном случае, если эмпирическое значение критерия оказывается строго больше критического, то нулевая гипотеза отвергается и принимается альтернативная гипотеза – характеристики экспериментальной и контрольной группы считаются раз- личными с достоверностью различий 1 – a . Например, если a = 0,05 и принята альтернативная гипоте- за, то достоверностьразличийравна 0,95 или 95%.
Другими словами, чем меньше эмпирическое значение критерия (чем левее оно находится от кри- тического значения), тем больше степень совпадения характеристик сравниваемых объектов. И наобо- рот, чем больше эмпирическое значение критерия (чем правее оно находится от критического значе- ния), тем сильнее различаются характеристики сравниваемых объектов.
В дальнейшем мы ограничимся уровнем значимости a = 0,05, поэтому, если эмпирическое значе- ние критерия оказывается меньше или равно критическому, то можно сделать вывод, что "ха- рактеристики экспериментальной и контрольной групп совпадают с уровнем значимости 0,05". Если эмпирическое значение критерия оказывается строго больше критического, то можно сде- лать вывод, что "достоверность различий характеристик экспериментальной и контрольной групп равна 95%".
Опишем методики расчета эмпирических значений критериев для двух типовых задач анализа дан- ных – сравнения выборок, содержащих данные, измеренные в шкале отношений и порядковой шкале.
Методика определения достоверности совпадений и различий для экспериментальных дан- ных, измеренных в шкале отношений. Рассмотрим случай (см. описание исходных данных выше в пятом разделе), когда для измерений используется шкала отношений. Предположим, что имеется экспе-
риментальная группа, состоящая из N человек, и контрольная группа, состоящая из M человек. Допус- тим, что в результате измерения одного и того же показателя с помощью одной и той же процедуры измерений были получены следующие данные: x = (x1, x2, …, xN) – выборка для экспериментальной группы и y = (y1, y2, …, yM) – выборка для контрольной группы, где xi– элемент выборки – значение исследуемого показателя у i-го члена экспериментальной группы, i = 1, 2, …, N, а yj– значение иссле- дуемого показателя у j-го члена контрольной группы, j = 1, 2, …, M. Так как измерения производились в шкале отношений, то {xi} и {yj} – положительные, в том числе, возможно – целые, числа, для которых имеют смысл все арифметические операции. В качестве примера будем рассматривать результаты из- мерений уровня знаний в контрольной и экспериментальной группах до и после эксперимента (см. таблицу 1) – количество правильно решенных задач.
23 Заметим,чтовматематическойстатистикеисторическисложилосьназыватьстатистическимикритерияминетолько решающие правила, но и методы расчета определенного числа (используемого в решающих правилах), а также самоэточисло.
Для данных, измеренных в шкале отношений, для проверки гипотезы о совпадении характеристик двух групп целесообразно использование либо критерия24 Крамера-Уэлча, либо критерия Вилкоксона-Манна-Уитни. Критерий Крамера-Уэлча предназначен для проверки гипотезы о равенстве средних (строго говоря – математических ожиданий) двух выборок, критерий Вилкоксона-Манна-Уитни25 явля- ется более "тонким" (но и более трудоемким) – он позволяет проверять гипотезу о том, что две выборки "одинаковы" (в том числе, что совпадают их средние, дисперсии и все другие показатели26).
Критерий Крамера-Уэлча. Эмпирическое значение данного критерия рассчитывается на основа-
нии информации об объемах N и М выборок x и y, выборочных средних xи yи выборочных диспер- сиях Dxи Dyсравниваемых выборок (эти значения могут быть вычислены вручную по формулам (1)-(2) или с помощью инструмента "Описательная статистика" в компьютерной программе Microsoft Excel для
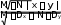Windows – см. выше) по следующей формуле:
Алгоритм определения достоверности совпадений и различий характеристик сравниваемых выбо- рок для экспериментальных данных, измеренных в шкале отношений, с помощью критерия Крамера- Уэлча заключается в следующем:
В качестве примера применим алгоритм для данных из таблицы 1.
Для этого сравним сначала числа правильно решенных задач в контрольной и экспериментальной группе до начала эксперимента. Вычисляем28 по формуле (3) значение Tэмп= 0,04 1,96. Следовательно, гипотеза о совпадении характеристик контрольной и экспериментальной групп до начала эксперимента принимается на уровне значимости 0,05.
Теперь сравним характеристики контрольной и экспериментальной групп после окончания экспе- римента. Вычисляем по формуле (3) значение Tэмп= 2,42 > 1,96. Следовательно, достоверность разли- чий характеристик контрольной и экспериментальной групп после окончания эксперимента составляет 95%.
Итак, начальные (до начала эксперимента)
состояния экспериментальной и контрольной групп сов- падают, а конечные (после окончания эксперимента) – различаются. Следовательно, можно сделать вывод, что эффект изменений обусловлен именно применением экспериментальной методики обучения. Отметим, что мы не рассматриваем вопрос о том, "в какую сторону" экспериментальная группа от- личается от контрольной, то есть, улучшились или ухудшились (с содержательной точки зрения, не имеющей отношения к статистическим методам и являющейся прерогативой педагогики) исследуемые
характеристики.
Общие подходы к определению достоверности совпадений и различий. Как отмечалось выше, типовой задачей анализа данных в педагогических исследованиях является установление совпадений или различий характеристик экспериментальной и контрольной группы. Для этого формулируются статистическиегипотезы:
-
гипотеза об отсутствии различий (так называемая нулеваягипотеза); -
гипотеза о значимости различий (так называемая альтернативнаягипотеза).
Для принятия решений о том, какую из гипотез (нулевую или альтернативную) следует принять, используют решающие правила – статистические критерии23. То есть, на основании информации о результатах наблюдений (характеристиках членов экспериментальной и контрольной группы) вычисля- ется число, называемое эмпирическим значением критерия. Это число сравнивается с известным (на- пример, заданным таблично) эталонным числом, называемым критическимзначением критерия.
Критические значения приводятся, как правило, для нескольких уровней значимости. Уровнем зна- чимости называется вероятность ошибки, заключающейся в отклонении (не принятии) нулевой гипоте- зы, то есть вероятность того, что различия сочтены существенными, а они на самом деле случайны. Обычно используют уровни значимости (обозначаемые a ), равные 0,05, 0,01 и 0,001. В педагогических исследованиях обычно ограничиваются значением 0,05, то есть, грубо говоря, допускается не более чем 5% возможность ошибки.
Если полученное исследователем эмпирическое значение критерия оказывается меньше или равно
критическому, то принимается нулевая гипотеза – считается, что на заданном уровне значимости (то есть при том значении a , для которого рассчитано критическое значение критерия) характеристики экспериментальной и контрольной групп совпадают. В противном случае, если эмпирическое значение критерия оказывается строго больше критического, то нулевая гипотеза отвергается и принимается альтернативная гипотеза – характеристики экспериментальной и контрольной группы считаются раз- личными с достоверностью различий 1 – a . Например, если a = 0,05 и принята альтернативная гипоте- за, то достоверностьразличийравна 0,95 или 95%.
Другими словами, чем меньше эмпирическое значение критерия (чем левее оно находится от кри- тического значения), тем больше степень совпадения характеристик сравниваемых объектов. И наобо- рот, чем больше эмпирическое значение критерия (чем правее оно находится от критического значе- ния), тем сильнее различаются характеристики сравниваемых объектов.
В дальнейшем мы ограничимся уровнем значимости a = 0,05, поэтому, если эмпирическое значе- ние критерия оказывается меньше или равно критическому, то можно сделать вывод, что "ха- рактеристики экспериментальной и контрольной групп совпадают с уровнем значимости 0,05". Если эмпирическое значение критерия оказывается строго больше критического, то можно сде- лать вывод, что "достоверность различий характеристик экспериментальной и контрольной групп равна 95%".
Опишем методики расчета эмпирических значений критериев для двух типовых задач анализа дан- ных – сравнения выборок, содержащих данные, измеренные в шкале отношений и порядковой шкале.
Методика определения достоверности совпадений и различий для экспериментальных дан- ных, измеренных в шкале отношений. Рассмотрим случай (см. описание исходных данных выше в пятом разделе), когда для измерений используется шкала отношений. Предположим, что имеется экспе-
риментальная группа, состоящая из N человек, и контрольная группа, состоящая из M человек. Допус- тим, что в результате измерения одного и того же показателя с помощью одной и той же процедуры измерений были получены следующие данные: x = (x1, x2, …, xN) – выборка для экспериментальной группы и y = (y1, y2, …, yM) – выборка для контрольной группы, где xi– элемент выборки – значение исследуемого показателя у i-го члена экспериментальной группы, i = 1, 2, …, N, а yj– значение иссле- дуемого показателя у j-го члена контрольной группы, j = 1, 2, …, M. Так как измерения производились в шкале отношений, то {xi} и {yj} – положительные, в том числе, возможно – целые, числа, для которых имеют смысл все арифметические операции. В качестве примера будем рассматривать результаты из- мерений уровня знаний в контрольной и экспериментальной группах до и после эксперимента (см. таблицу 1) – количество правильно решенных задач.
23 Заметим,чтовматематическойстатистикеисторическисложилосьназыватьстатистическимикритерияминетолько решающие правила, но и методы расчета определенного числа (используемого в решающих правилах), а также самоэточисло.
Для данных, измеренных в шкале отношений, для проверки гипотезы о совпадении характеристик двух групп целесообразно использование либо критерия24 Крамера-Уэлча, либо критерия Вилкоксона-Манна-Уитни. Критерий Крамера-Уэлча предназначен для проверки гипотезы о равенстве средних (строго говоря – математических ожиданий) двух выборок, критерий Вилкоксона-Манна-Уитни25 явля- ется более "тонким" (но и более трудоемким) – он позволяет проверять гипотезу о том, что две выборки "одинаковы" (в том числе, что совпадают их средние, дисперсии и все другие показатели26).
Критерий Крамера-Уэлча. Эмпирическое значение данного критерия рассчитывается на основа-
нии информации об объемах N и М выборок x и y, выборочных средних xи yи выборочных диспер- сиях Dxи Dyсравниваемых выборок (эти значения могут быть вычислены вручную по формулам (1)-(2) или с помощью инструмента "Описательная статистика" в компьютерной программе Microsoft Excel для
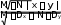Windows – см. выше) по следующей формуле:-
Tэмп= .
Алгоритм определения достоверности совпадений и различий характеристик сравниваемых выбо- рок для экспериментальных данных, измеренных в шкале отношений, с помощью критерия Крамера- Уэлча заключается в следующем:
-
Вычислить для сравниваемых выборок Tэмп– эмпирическое значение критерия Крамера-Уэлча по формуле (3). -
Сравнить это значение с критическим значением T0.05 = 1,96: если Tэмп1,96, то сделать вывод: "характеристики сравниваемых выборок совпадают на уровне значимости 0,05"; если Tэмп > 1,96, то сделать вывод "достоверность различий характеристик сравниваемых выборок составляет27 95%".
В качестве примера применим алгоритм для данных из таблицы 1.
Для этого сравним сначала числа правильно решенных задач в контрольной и экспериментальной группе до начала эксперимента. Вычисляем28 по формуле (3) значение Tэмп= 0,04 1,96. Следовательно, гипотеза о совпадении характеристик контрольной и экспериментальной групп до начала эксперимента принимается на уровне значимости 0,05.
Теперь сравним характеристики контрольной и экспериментальной групп после окончания экспе- римента. Вычисляем по формуле (3) значение Tэмп= 2,42 > 1,96. Следовательно, достоверность разли- чий характеристик контрольной и экспериментальной групп после окончания эксперимента составляет 95%.
Итак, начальные (до начала эксперимента)
состояния экспериментальной и контрольной групп сов- падают, а конечные (после окончания эксперимента) – различаются. Следовательно, можно сделать вывод, что эффект изменений обусловлен именно применением экспериментальной методики обучения. Отметим, что мы не рассматриваем вопрос о том, "в какую сторону" экспериментальная группа от- личается от контрольной, то есть, улучшились или ухудшились (с содержательной точки зрения, не имеющей отношения к статистическим методам и являющейся прерогативой педагогики) исследуемые
характеристики.