Файл: Методические указания по написанию курсовой и выпускной квалификационной работы студентов, обучающихся по направлению Клиническая психология.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 70
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
диаграмма, представленная в виде гистограммы, ленточной или круговой диаграммы, и график.
Все рисунки, помещенные в основной текст работы, имеют сквозную нумерацию. Если в работе только один рисунок, то он не нумеруется.
Указание на порядковый номер рисунка содержит:
- сокращенное слово «Рис.», выполненное с прописной буквы с абзацным отступом;
- число, выполненное арабскими цифрами, соответствующее порядковому номеру в работе.
Знак «№» не ставится.
Рисунок обязательно имеет наименование. Нумерация и наименование иллюстраций помещаются под изображением с выравниванием «по центру» и выполняются теми же шрифтом и размером, что и основной текст. Допускается его выделение курсивом. Точка в конце наименования рисунка не ставится. Связь рисунка с текстом оформляется в виде ссылок с указанием порядкового номера, аналогично ссылке на таблицу.
Графикпредставляет собой условное изображение величин и их соотношений, выполняется в системе координат, оси которой представляют собой шкалы с выбранными и обозначенными единичными отрезками. Как правило, горизонтальная ось отражает время или независимые качественные и независимые переменные. Вертикальная ось представляет количественные характеристики рассматриваемых объектов или показателей на определенный период времени. Эти характеристики наглядно изображаются точками, которые соединяются отрезками или сглаженными кривыми.
Если график содержит информацию о нескольких группах однородных данных, то для изображения применяют линии разных цветов, конфигураций, толщины. Расшифровка использованных условных обозначений носит название легенды и размещается справа от рисунка. Слово «примечание» выполняется с новой строки с абзацным отступом вразрядку, после него ставится точка.
Диаграмма отражает зависимость между величинами, позволяет сравнивать и анализировать массовые данные. Прим. В тексте работы недопустимо использование цветных диаграмм.
- Гистограмма (столбиковая диаграмма) позволяет представить изменение данных на протяжении отрезка времени или наглядно сравнить различные величины. Одинаково часто применяются плоскостные и объемные гистограммы, отличия между ними несущественны.
Гистограмма, как и график, выполняется в системе координат. По горизонтали в гистограмме располагается ось категорий, по вертикали - ось значений. Изображение осей, подписей к ним аналогичны правилам оформления графиков, рассмотренным выше.
В связи с тем, что основной задачей гистограммы является наглядное сопоставление данных, то на одном рисунке подобного типа могут быть размещены данные о двух и более распределениях.
- Ленточная (линейчатая) диаграмма позволяет сравнивать отдельные значения, обращая большее внимание на сравниваемые значения, чем на временные промежутки.
Этот тип диаграмм тоже выполняется в системе координат, оси которой представляют собой шкалы с выбранными и обозначенными единичными отрезками. В отличие от гистограммы, по горизонтали в линейчатой диаграмме располагается ось значений, по вертикали - ось категорий. В остальном правила их оформления аналогичны.
- Круговая диаграмма показывает отношение размеров элементов, образующих ряд данных, к сумме элементов. Этот тип диаграмм представляет собой круг, разделенный на секторы, размеры которых пропорциональны величинам изображаемых объектов. В круговой диаграмме всегда отображается только один ряд данных. Важно, что сумма элементов, представляемых круговой диаграммой всегда должна быть равна 100% или одной целой. Поэтому результаты анкетирования с допущением множества ответов на каждый вопрос не могут быть представлены в подобном виде.
Для облегчения работы с маленькими секторами в основной круговой диаграмме их можно объединить в один элемент, а затем разбить в отдельную диаграмму рядом с основной.
2.2 Статистическая обработка результатов исследования
Применение методов математической статистики (статистических методов) для обработки результатов эмпирического исследования является обязательным требованием к курсовым и выпускным квалификационным работам по клинической психологии.
Методами статистической обработки результатов исследования называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе исследования, можно обобщать, приводить в систему, выявляя скрытые в них закономерности.
В зависимости от применяемых методов можно охарактеризовать выборочное распределение данных исследования, можем судить о динамики изменения отдельных показателей, о статистических связях существующих между исследуемыми переменными величинами.
Математическая обработка результатов исследования дает клиническому психологу возможность ответить на ряд вопросов:
- Чем один человек отличается от другого (или группы лиц) по исследуемой психологической характеристике?
- Чем отличается уровень развития одной психологической характеристики от другой у данной личности?
- Как развиваются две группы лиц по какой-либо психологической характеристике и др.
Ответы на эти и другие вопросы могут быть получены в ходе психодиагностического обследования и зависят от правильного проведения этого обследования, а также от грамотной обработки и интерпретации полученных результатов.
Главная цель статистических методов - представить количественные данные в сжатой форме, с тем, чтобы облегчить их понимание.
Все методы статистического анализа условно делятся на первичные и вторичные.
Первичными называются методы, с помощью которых можно получить показатели, непосредственно отражающие результаты проводимых в эксперименте измерений. Под первичными статистическими показателями имеются в виду показатели, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов диагностики.
К первичным методам статистической обработки относят: определение среднего арифметического, дисперсии, моды и медианы.
Вторичными называют методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.
К вторичным методам статистической обработки относят: корреляционный анализ, регрессионный анализ, факторный анализ, методы сравнения первичных данных двух или нескольких выборок.
2.2.1 Первичные методы статистической обработки
Меры центральной тенденции
Рассматривая методы математической статистики, применяемые для обработки данных тестовых исследований, можно выделить группу методов которые могут описывать те или иные меры центральной тенденции. Такие меры указывают наиболее типичный результат, характеризующий выполнение теста всей группой. Самая известная из таких мер - среднеарифметическое значение (М).
Среднеарифметическое (или выборочное среднее) значение представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута исследованию (выборка испытуемых). Сравнивая среднее значение двух или нескольких групп, мы можем судить об относительной степени развития у людей, составляющих эти группы, оцениваемого качества.
Другой мерой центральной тенденции является мода (Мо) - наиболее часто встречающийся результат. В интервальном частотном распределении мода определяется как середина интервала, для которого частота максимальна.
Пример: В ряду значений 2, 3, 4, 5, 5, 6, 6, 6, 7, 7, 8, 9 модой является 6, потому, что 6 встречается чаще любого другого числа.
Третья мера центральной тенденции - медиана (Ме), - результат, находящийся в середине последовательности показателей, если их расположить в порядке возрастания или убывания. Справа и слева от медианы (Ме) в упорядоченном ряду остается по одинаковому количеству данных (50% и 50%). Если ряд включает в себя четное количество признаков, то медианой (Ме) будет среднее, взятое как полусумма двух центральных значений ряда.
Значения Ме и Мо полезны для того, чтобы установить является ли распределение частных значений изучаемого признака симметричным и приближающимся к нормальному распределению. Среднее арифметическое (М), медиана (Ме) и мода (Мо) для нормального распределения обычно совпадают или очень мало отличаются друг от друга. При нормальном распределении результатов график распределения имеет форму колокола (рис. 1).
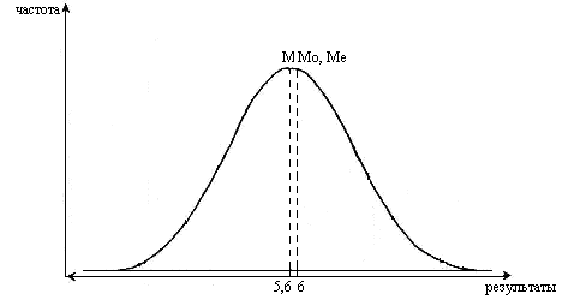
Рис. 1. График нормального распределения результатов исследования
Меры разброса данных
Для более полного описания результатов эмпирического исследования используются меры разброса данных, характеризующие степень индивидуальных отклонений от центральной тенденции. Это самый простой показатель, который можно получить для выборки - разность между максимальной и минимальной величинами данного конкретного вариационного ряда. Мера разброса данных позволяет сравнивать между собой разные группы. Чем сильней варьирует измеряемый признак, тем больше величина разброса данных и наоборот.
Необходимо отметить, что данная мера крайне неточна и неустойчива. Единственный необычно высокий или низкий результат может повлиять на величину размаха.
Более точный метод измерения разброса данных основан на учете разности между каждым индивидуальным результатом и среднеарифметическим значением по группе. Такой мерой разброса является дисперсия или средний квадрат отклонения.
Дисперсия характеризует насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонение или разброс данных.
2.2.2 Методы вторичной статистической обработки
результатов исследования
С помощью вторичных методов статистической обработки данных проверяются, доказываются или опровергаются гипотезы, связанные с эмпирическим исследованием.
Чаще всего в прикладных клинико-психологических исследованиях применяются следующие методы вторичной статистической обработки результатов:
- Методы сравнения двух или нескольких элементарных статистик (средних, дисперсий и т. д.) относящихся к разным выборкам.
- Методы установления статистических связей между переменными (корреляционный анализ).
- Методы выявления внутренней статистической структуры эмпирических данных (факторный анализ).
В общем, психологические задачи, решаемые с помощью методов математической статистики, условно можно разделить на несколько групп.
- Задачи, требующие установления сходства или различия.
- Задачи, требующие группировки и классификации данных.
- Задачи, ставящие целью анализ источников вариативности (изменчивости) получаемых психологических признаков.
- Задачи, предполагающие возможность прогноза на основе имеющихся данных.
Далее будут рассмотрены основные статистические методы используемые в студенческих работах.
Статистические критерии различий
Одной из наиболее встречающихся статистических задач, с которыми сталкивается клинический психолог, является задача сравнения результатов обследования какого-либо психологического признака в разных условиях измерения (например, до и после определенного воздействия) или обследования контрольной и экспериментальной групп. Также нередко возникает необходимость оценить характер изменения того или иного психологического показателя в одной или нескольких группах в разные периоды времени или выявить динамику изменения этого показателя под влиянием экспериментальных воздействий. Для решения подобных задач используется большой выбор статистических способов, называемых в наиболее общем виде критериями различий. Эти критерии позволяют оценить степень статистической достоверности различий между разнообразными показателями. Важно учитывать, что уровень достоверности различий включается в план проведения эксперимента.
Существует достаточно большое количество критериев различий. Каждый из них имеет свою специфику, различаясь между собой по основаниям (например, тип измерительной шкалы, максимальный объем выборки, количество выборок, качество выборки - зависимая и независимая).
Все рисунки, помещенные в основной текст работы, имеют сквозную нумерацию. Если в работе только один рисунок, то он не нумеруется.
Указание на порядковый номер рисунка содержит:
- сокращенное слово «Рис.», выполненное с прописной буквы с абзацным отступом;
- число, выполненное арабскими цифрами, соответствующее порядковому номеру в работе.
Знак «№» не ставится.
Рисунок обязательно имеет наименование. Нумерация и наименование иллюстраций помещаются под изображением с выравниванием «по центру» и выполняются теми же шрифтом и размером, что и основной текст. Допускается его выделение курсивом. Точка в конце наименования рисунка не ставится. Связь рисунка с текстом оформляется в виде ссылок с указанием порядкового номера, аналогично ссылке на таблицу.
Графикпредставляет собой условное изображение величин и их соотношений, выполняется в системе координат, оси которой представляют собой шкалы с выбранными и обозначенными единичными отрезками. Как правило, горизонтальная ось отражает время или независимые качественные и независимые переменные. Вертикальная ось представляет количественные характеристики рассматриваемых объектов или показателей на определенный период времени. Эти характеристики наглядно изображаются точками, которые соединяются отрезками или сглаженными кривыми.
Если график содержит информацию о нескольких группах однородных данных, то для изображения применяют линии разных цветов, конфигураций, толщины. Расшифровка использованных условных обозначений носит название легенды и размещается справа от рисунка. Слово «примечание» выполняется с новой строки с абзацным отступом вразрядку, после него ставится точка.
Диаграмма отражает зависимость между величинами, позволяет сравнивать и анализировать массовые данные. Прим. В тексте работы недопустимо использование цветных диаграмм.
- Гистограмма (столбиковая диаграмма) позволяет представить изменение данных на протяжении отрезка времени или наглядно сравнить различные величины. Одинаково часто применяются плоскостные и объемные гистограммы, отличия между ними несущественны.
Гистограмма, как и график, выполняется в системе координат. По горизонтали в гистограмме располагается ось категорий, по вертикали - ось значений. Изображение осей, подписей к ним аналогичны правилам оформления графиков, рассмотренным выше.
В связи с тем, что основной задачей гистограммы является наглядное сопоставление данных, то на одном рисунке подобного типа могут быть размещены данные о двух и более распределениях.
- Ленточная (линейчатая) диаграмма позволяет сравнивать отдельные значения, обращая большее внимание на сравниваемые значения, чем на временные промежутки.
Этот тип диаграмм тоже выполняется в системе координат, оси которой представляют собой шкалы с выбранными и обозначенными единичными отрезками. В отличие от гистограммы, по горизонтали в линейчатой диаграмме располагается ось значений, по вертикали - ось категорий. В остальном правила их оформления аналогичны.
- Круговая диаграмма показывает отношение размеров элементов, образующих ряд данных, к сумме элементов. Этот тип диаграмм представляет собой круг, разделенный на секторы, размеры которых пропорциональны величинам изображаемых объектов. В круговой диаграмме всегда отображается только один ряд данных. Важно, что сумма элементов, представляемых круговой диаграммой всегда должна быть равна 100% или одной целой. Поэтому результаты анкетирования с допущением множества ответов на каждый вопрос не могут быть представлены в подобном виде.
Для облегчения работы с маленькими секторами в основной круговой диаграмме их можно объединить в один элемент, а затем разбить в отдельную диаграмму рядом с основной.
2.2 Статистическая обработка результатов исследования
Применение методов математической статистики (статистических методов) для обработки результатов эмпирического исследования является обязательным требованием к курсовым и выпускным квалификационным работам по клинической психологии.
Методами статистической обработки результатов исследования называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе исследования, можно обобщать, приводить в систему, выявляя скрытые в них закономерности.
В зависимости от применяемых методов можно охарактеризовать выборочное распределение данных исследования, можем судить о динамики изменения отдельных показателей, о статистических связях существующих между исследуемыми переменными величинами.
Математическая обработка результатов исследования дает клиническому психологу возможность ответить на ряд вопросов:
- Чем один человек отличается от другого (или группы лиц) по исследуемой психологической характеристике?
- Чем отличается уровень развития одной психологической характеристики от другой у данной личности?
- Как развиваются две группы лиц по какой-либо психологической характеристике и др.
Ответы на эти и другие вопросы могут быть получены в ходе психодиагностического обследования и зависят от правильного проведения этого обследования, а также от грамотной обработки и интерпретации полученных результатов.
Главная цель статистических методов - представить количественные данные в сжатой форме, с тем, чтобы облегчить их понимание.
Все методы статистического анализа условно делятся на первичные и вторичные.
Первичными называются методы, с помощью которых можно получить показатели, непосредственно отражающие результаты проводимых в эксперименте измерений. Под первичными статистическими показателями имеются в виду показатели, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов диагностики.
К первичным методам статистической обработки относят: определение среднего арифметического, дисперсии, моды и медианы.
Вторичными называют методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.
К вторичным методам статистической обработки относят: корреляционный анализ, регрессионный анализ, факторный анализ, методы сравнения первичных данных двух или нескольких выборок.
2.2.1 Первичные методы статистической обработки
Меры центральной тенденции
Рассматривая методы математической статистики, применяемые для обработки данных тестовых исследований, можно выделить группу методов которые могут описывать те или иные меры центральной тенденции. Такие меры указывают наиболее типичный результат, характеризующий выполнение теста всей группой. Самая известная из таких мер - среднеарифметическое значение (М).
Среднеарифметическое (или выборочное среднее) значение представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута исследованию (выборка испытуемых). Сравнивая среднее значение двух или нескольких групп, мы можем судить об относительной степени развития у людей, составляющих эти группы, оцениваемого качества.
Другой мерой центральной тенденции является мода (Мо) - наиболее часто встречающийся результат. В интервальном частотном распределении мода определяется как середина интервала, для которого частота максимальна.
Пример: В ряду значений 2, 3, 4, 5, 5, 6, 6, 6, 7, 7, 8, 9 модой является 6, потому, что 6 встречается чаще любого другого числа.
Третья мера центральной тенденции - медиана (Ме), - результат, находящийся в середине последовательности показателей, если их расположить в порядке возрастания или убывания. Справа и слева от медианы (Ме) в упорядоченном ряду остается по одинаковому количеству данных (50% и 50%). Если ряд включает в себя четное количество признаков, то медианой (Ме) будет среднее, взятое как полусумма двух центральных значений ряда.
Значения Ме и Мо полезны для того, чтобы установить является ли распределение частных значений изучаемого признака симметричным и приближающимся к нормальному распределению. Среднее арифметическое (М), медиана (Ме) и мода (Мо) для нормального распределения обычно совпадают или очень мало отличаются друг от друга. При нормальном распределении результатов график распределения имеет форму колокола (рис. 1).

Рис. 1. График нормального распределения результатов исследования
Меры разброса данных
Для более полного описания результатов эмпирического исследования используются меры разброса данных, характеризующие степень индивидуальных отклонений от центральной тенденции. Это самый простой показатель, который можно получить для выборки - разность между максимальной и минимальной величинами данного конкретного вариационного ряда. Мера разброса данных позволяет сравнивать между собой разные группы. Чем сильней варьирует измеряемый признак, тем больше величина разброса данных и наоборот.
Необходимо отметить, что данная мера крайне неточна и неустойчива. Единственный необычно высокий или низкий результат может повлиять на величину размаха.
Более точный метод измерения разброса данных основан на учете разности между каждым индивидуальным результатом и среднеарифметическим значением по группе. Такой мерой разброса является дисперсия или средний квадрат отклонения.
Дисперсия характеризует насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонение или разброс данных.
2.2.2 Методы вторичной статистической обработки
результатов исследования
С помощью вторичных методов статистической обработки данных проверяются, доказываются или опровергаются гипотезы, связанные с эмпирическим исследованием.
Чаще всего в прикладных клинико-психологических исследованиях применяются следующие методы вторичной статистической обработки результатов:
- Методы сравнения двух или нескольких элементарных статистик (средних, дисперсий и т. д.) относящихся к разным выборкам.
- Методы установления статистических связей между переменными (корреляционный анализ).
- Методы выявления внутренней статистической структуры эмпирических данных (факторный анализ).
В общем, психологические задачи, решаемые с помощью методов математической статистики, условно можно разделить на несколько групп.
- Задачи, требующие установления сходства или различия.
- Задачи, требующие группировки и классификации данных.
- Задачи, ставящие целью анализ источников вариативности (изменчивости) получаемых психологических признаков.
- Задачи, предполагающие возможность прогноза на основе имеющихся данных.
Далее будут рассмотрены основные статистические методы используемые в студенческих работах.
Статистические критерии различий
Одной из наиболее встречающихся статистических задач, с которыми сталкивается клинический психолог, является задача сравнения результатов обследования какого-либо психологического признака в разных условиях измерения (например, до и после определенного воздействия) или обследования контрольной и экспериментальной групп. Также нередко возникает необходимость оценить характер изменения того или иного психологического показателя в одной или нескольких группах в разные периоды времени или выявить динамику изменения этого показателя под влиянием экспериментальных воздействий. Для решения подобных задач используется большой выбор статистических способов, называемых в наиболее общем виде критериями различий. Эти критерии позволяют оценить степень статистической достоверности различий между разнообразными показателями. Важно учитывать, что уровень достоверности различий включается в план проведения эксперимента.
Существует достаточно большое количество критериев различий. Каждый из них имеет свою специфику, различаясь между собой по основаниям (например, тип измерительной шкалы, максимальный объем выборки, количество выборок, качество выборки - зависимая и независимая).