ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 295
Скачиваний: 3
Основные формулы
1.Электростатическое поле в вакууме.1.1.Закон Кулона ,или где F – сила взаимодействия между двумя точечными зарядами q1 и q2 в вакууме; ε0=8,85·10-12 Ф/м – электрическая постоянная; k=9·109 м/Ф, r - расстояние между зарядами.1.2.Закон сохранения заряда -алгебраическая сумма зарядов тел, образующих изолиро-ванную систему, равна нулю. 1.3.Напряженность электрического поля ,где - сила, действующая на точечный пробный заряд , помещенный в данную точку поля.1.4.Потенциал электрического поля ,где W – потенциальная энергия точечного пробного заряда , помещенного в данную точку поля.1.5.Работа сил по перемещению заряда из точки поля с потенциалом φ1в точку с потенциалом φ2A=q·(φ1-φ2)=q·U,где U – разность потенциалов электрического поля в начальной и конечной точках. 1.6.Напряженность Е и потенциал φ поля точечного заряда , 1.7.Напряженность и потенциал φ связаны между собой соотношением: или 1.8.Принцип суперпозиции (наложения) полей ,
,
где 
- напряженность, φ – потенциал поля, созданного
системой зарядов.
1.9.Теорема Остроградского-Гаусса: поток вектора напряженности 
через произвольную замкнутую поверхность S равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0,
.
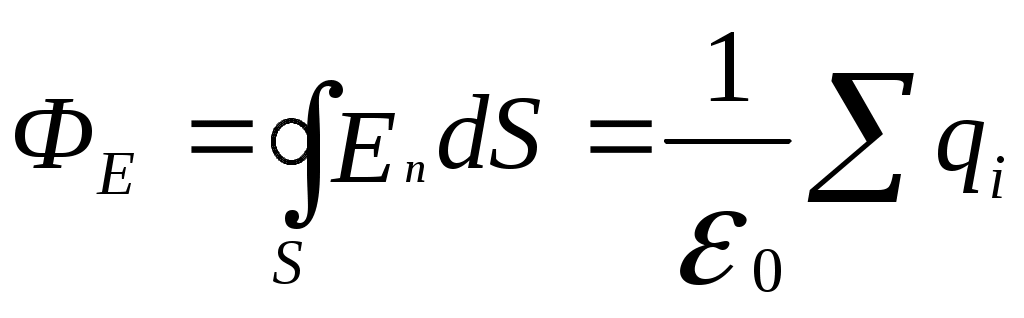1.10.Напряженность электрического поля, создаваемого проводящей сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:
а) внутри сферы (r < R) E = 0;
б) на поверхности сферы (r = R) 
в) вне сферы (r > R) 
1.11.Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси 
,
где 
-линейная плотность заряда нити (цилиндра).
1.12.Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью 
,
где 
- поверхностная плотность заряда плоскости.
1.13.Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями с одинаковой по модулю поверхностной плотностью заряда (поле плоского конденсатора):
2. Диэлектрики в электрическом поле
2.1.Индукция электрического поля (электрическое смещение)
,
где 
- поляризованность диэлектрика.
2.2.Теорема Остроградского-Гаусса для индукции электрического поля (электрического смещения):
,
где 
-алгебраическая сумма свободных зарядов, находящихся внутри поверхности S.
2.3.Напряженность электрического поля в диэлектрике и поляризованность 
диэлектрика связаны соотношением =ε0 (ε-1)
где ε=Е0/Е диэлектрическая проницаемость диэлектрика.
2.4. Связь индукции и напряженности электрического поля 
2.5.Связь напряженности электрического поля 
в диэлектрике с напряженностью поля свободных 
и связанных 
зарядов 
2.6.Поверхностная плотность связанных зарядов
где Рn и En - нормальные составляющие поляризованноcти диэлектрика и напряженности электрического поля.
3. Проводники в электростатическом поле.
3.1.Условие равновесия зарядов в проводнике:
, φ= const,
где 
- напряженность электрического поля в произвольной точке внутри проводника, φ – потенциал произвольной точки проводника.
3.2.Электроемкость проводника
С=q/φ,
где q -заряд проводника, φ - потенциал поверхности проводника.
3.3.Электроемкость уединенной проводящей сферы радиуса R
С=4πεε0R,
где R – радиус сферы, ε-диэлектрическая проницаемость среды, в которой находится проводник.
3.4.Электроемкость конденсатора
С=q/U,
где q – заряд одной из обкладок, U – разность потенциалов между обкладками конденсатора.
3.5. Электроемкость плоского конденсатора
,где S - площадь одной пластины; d- расстояние между пластинами, ε – диэлектрическая проницаемость диэлектрика, находящегося между пластинами конденсатора.3.6.Электроемкость батареи конденсаторов а) при последовательном соединении ;б) при параллельном соединении .3.7.Энергия заряженного конденсатора3.8.Объемная плотность энергии электрического поля .4. Постоянный ток.4.1.Сила тока I=dq/dt,где q - заряд прошедший через поперечное сечение за время dt/4.2.Плотность тока j=I/S, где S - площадь поперечного сечения проводника. 4.3.Связь плотности тока со средней скоростью направленного движения заряженных частиц , где е- заряд частицы; n-концентрация заряженных частиц.4.5.Закон Омаа) Для участка цепи I=U/R,где U – напряжение, R - сопротивление участка;б) для замкнутой цепи ,где E - э.д.с. источника тока, R – внешнее сопротивление цепи, r- внутреннее сопротивление источника тока.в) закон Ома в дифференциальной формегде σ - удельная теплопроводность, - напряженность электрического поля в проводнике.4.6.Сопротивление однородного проводника постоянного поперечного сечения , где ρ - удельное сопротивление; l – длина, S - площадь поперечного сечения проводника.4.7.Зависимость удельного сопротивления металлов от температуры
,
где ρ0 – удельное сопротивление металла при t0=00С, t – температура по шкале Цельсия, α – температурный коэффициент сопротивления.
4.8.Правила Кирхгофа:
а)первое правило: алгебраическая сумма сил токов, сходящихся в узле равна нулю
б)второе правило: в произвольном замкнутом контуре разветвленной электрической цепи алгебраическая сумма произведений сил токов на сопротивления участков (
) равна алгебраической сумме э.д.с. (
).
.
4.9. Работа и мощность тока
4.10. Закон Джоуля-Ленца dQ=dA.
4.11.Закон Джоуля-Ленца в дифференциальной форме
Pуд= σЕ2.
Примеры решения задач.
Пример 1. Два точечных электрических заряда q1= 1кКл и q2= -2 кКл находятся в вакууме на расстоянии d= 10 см друг от друга. Определить напряженность Е и потенциал φ поля этих зарядов в точке А, удаленной от заряда q1 на расстояние r1=9 см и от заряда q2 на r2=7см.
Решение. Согласно принципу суперпозиции электрических полей напряженность электрического поля равна геометрической сумме напряженностей 
и 
полей, создаваемых каждым зарядом в отдельности:
. Напряженности электрических полей, создаваемых зарядами q1 и q2, равны: 
; 
(1)
Вектор
(рис. 1) направлен по силовой линии от заряда q1, так как заряд q1 положителен; вектор