направлен к заряду q₂, так как заряд q₂ отрицателен.

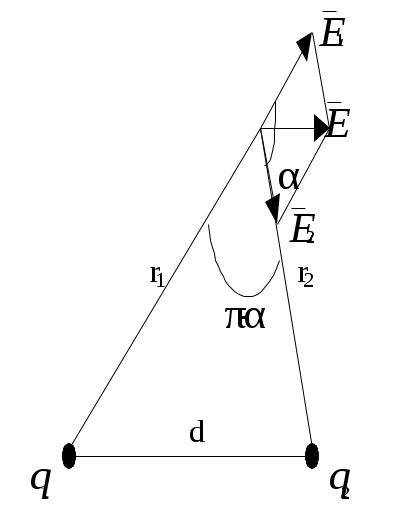Рис. 1

Модуль вектора E найдем по теореме косинусов:

(2)

где α - угол между векторами и , который может быть найден из треугольника со сторонами r₁, r₂, d:

.

Подставляя данные, получаем:



Подставляя выражения E₁ и E₂ из формул (1) в (2), получим

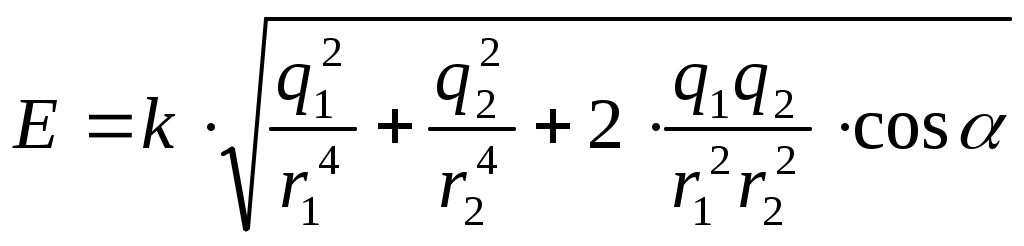(3)

Подставим значения величин в формулу (3) и произведем вычисления:

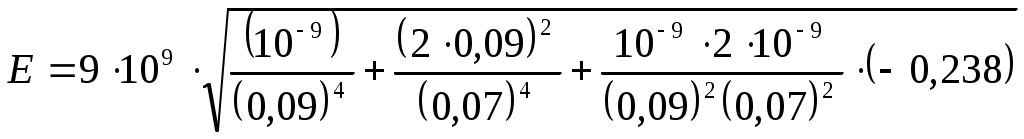= 3,58·10³ В/м = 3,58 кВ/м.

В соответствии с принципом суперпозиции электрических полей потенциал φ результирующего поля, создаваемого двумя зарядами q₁ и q₂ равен алгебраической сумме потенциалов, т. е.

φ = φ₁ + φ₂ (4)

Потенциал электрического поля, создаваемого в вакууме точечным зарядом q на расстоянии r от него, выражается формулой

(5)

Согласно формулам (4) и (5) получим

,или .

Подставив в это выражение значения физических величин, получим


Пример 2. Точечный заряд q = 25·10^-9 Кл находятся в поле, создаваемом прямым бесконечным цилиндром радиусом

R=10^-2м, равномерно заряженным с поверхностной плотностью заряда σ =25·10^-6 Кл/м². Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r= 0,1 м.

Решение. Сила, действующая на заряд q, находящийся в электрическом поле поле

---

F= qE (1)

где E - напряженность поля в точке, в которой находится заряд. Напряженность поля бесконечно длинного равномерно заряженного цилиндра равна

(2)

Выразим линейную плотность заряда τ через поверхностную плотность σ. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд q₁ двумя способами:

q₁ = σS =σ2πRl и q₁ = τl.

Приравняв прямые части этих равенств, получим

τl = 2πRlσ  τ = 2πRσ

С учетом этого формула (2) примет вид

Подставив это выражение E в формулу (2) получим искомую силу:

(3)

F =25 ·10^-9· 2· 10^-6 ·10^-2/(8,85· 10^-12 ·1·0 10^-12) = 565 ·10^-6 Н

Направление силы совпадает с направлением вектора , а последний в силу симметрии направлен перпендикулярно цилиндру.
Примеp 3. По тонкой нити, изогнутойпо дуге окружности, равномерно распределен заряд с линейной плотностью τ=10нКл/м. Определить напряженность Е и потенциал φэлектрического поля, создаваемого таким распределенным зарядом в точке, совпадавшей с центром кривизны дуги. Длина нити l составляет одну треть длины окружности и равна 15 см.

Решение. Выберем оси координат X и Y так, чтобы начало координат совпадало с центром кривизны дуги, а ось Y была бы симметрично расположена, относительно концов дуги (рис.2). Выделим элемент нити длиной dl.

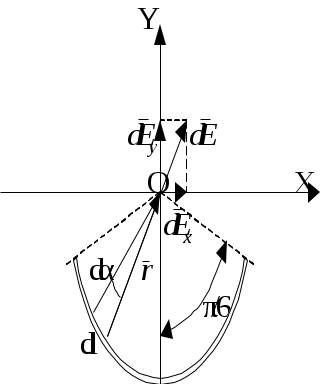Рис.2.

Заряд dq =τ·dl, находя­щийся на выделенном участке, можно считать точеч-ным.

Определим на-пряженность электрического поля в точке О. Для этого, най-дем напряжен-ность поля, создаваемого зарядом dq:

,

где - радиус-вектор, направленный от элемента dl к точке, в которой вычисляется напряженность.

---

Напряженность поля, создаваемого всей нитью в соответствии с принципом суперпозиции равна



Интегрирование ведется вдоль дуги, образованной нитью.

Выразим вектор через составляющие и на оси координат:



Тогда



В силу симметрии интеграл равен нулю, тогда

, или , (1)

где .
Так как r=const, dl=rdα, то


Отсюда



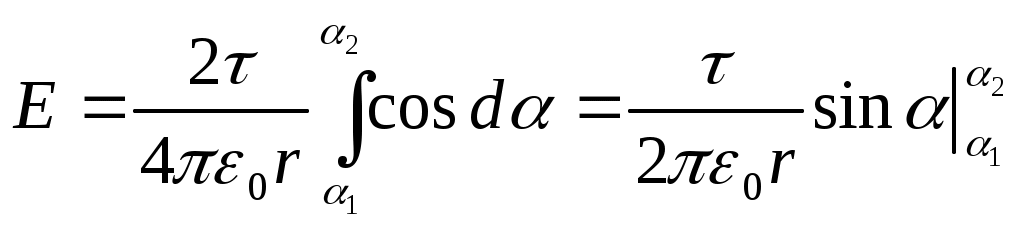
Здесь принято во внимание симметричное расположение дуги относительно оси У, и поэтому интегрирование проводится по половине дуги (от α₁=0 до α₂=π/6) а ре­зультат удваивается.

Подставив пределы и выразив через длину дуги (3·l=2πr), получим



Подставим значение τ и l в полученную формулу и вычислим:



Найдем потенциал электрического поля вточке. Сначала найдем потенциал dφ , создаваемый точечным зарядом dQв точке O:



Интегрируя, получим:



Так как l=2 πr/3, то

Произведем вычисления:

В.
Пример 4. Два бесконечных тонкостенных коаксиальных цилиндра радиусами R

---

₁=5см и R₂=10см равномерно заряжены с поверхностными плотностями зарядов равными, соответственно, σ₁=10^-8Кл/м² и σ₂= -3·10^-8 Кл/м² (рис.3). Пространство между цилиндрами заполнено парафином (ε=2). Определить напряженность поля в точках, находящихся на расстояниях: r₁=2 см; r₂=6см; r₃=15 см от оси цилиндра.

Решение. Воспользуемся теоремой Остроградского-Гаусса для индукции электрического поля и связью индукции и напряженности электрического поля:

, .

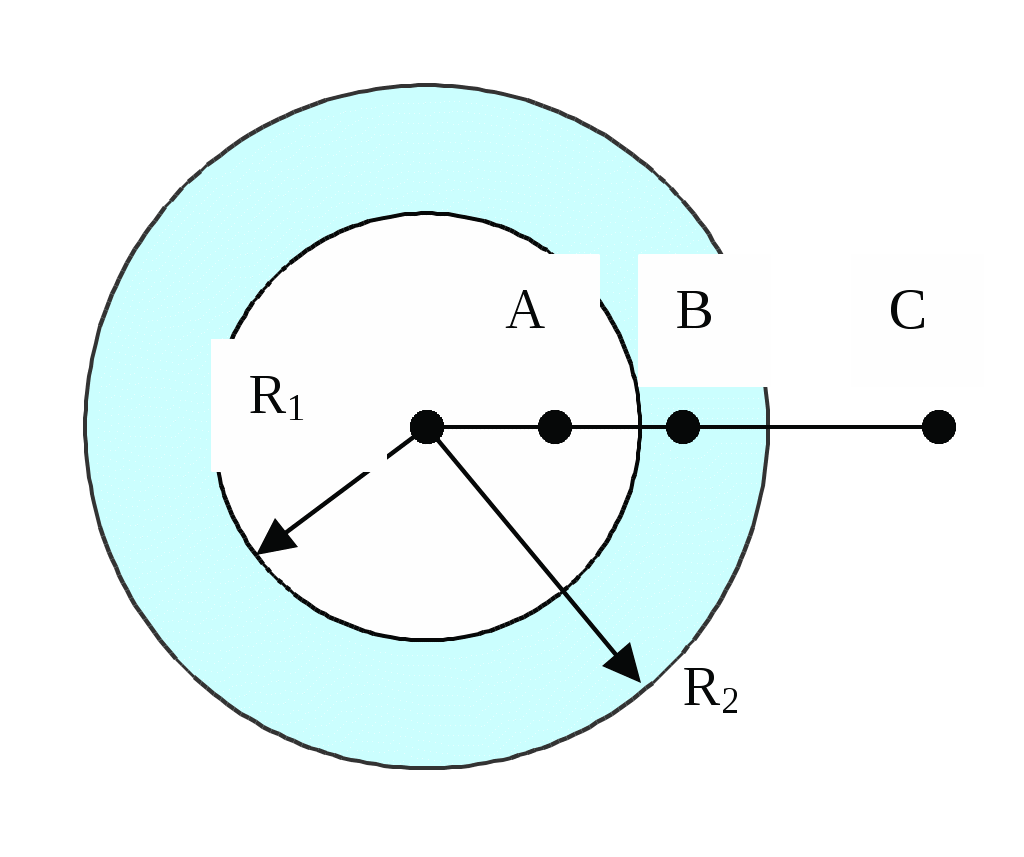Рис.3

Легко видеть, что индукция в точке А (на расстоянии r₁=2 см от оси) равна 0 (заряды внут-ри цилин-дрической поверхности S₁, проходя-щей через точку А, отсутствуют).

Индукция в точке B определяется только зарядами, находящимися на внутреннем цилиндре. Ее можно найти по формуле:

, (1)

где τ₁ – линейная плотность заряда внутреннего цилиндра:

. Отсюда



Подставляя численные данные, получим E₂ = 4,7 10²В/м.

Для точки С находим индукцию D₃ по принципу суперпозиции:

D₃ = D₁(r₃)-D₂(r₃), (2)

где D₁(r₃) – индукция поля, создаваемого внутренним цилиндром, D₂(r₃) – индукция поля, создаваемого внешним цилиндром в точке С. Находя D₁ и D₂, аналогично (1), и подставляя в (2) получим

,

отсюда .

Подставляя численные данные, получим Е₃= 1,5 10² В/м.
Пример 5. Электрическая цепь состоит из двух гальванических элементов, трех сопротивлений и гальванометра (рис.4).

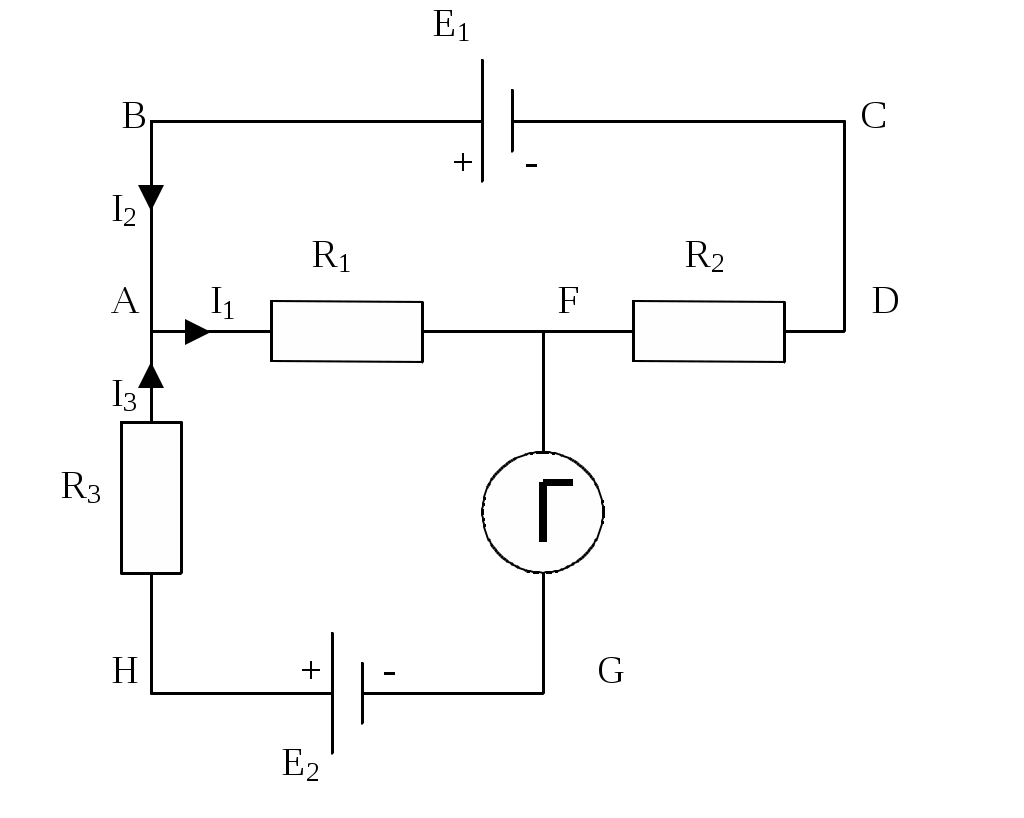Рис.4

---

Вэтой цепи r₁= 100 Ом, r₂₌50 Ом, r₃=20 Ом, Э.Д.С. элемента E₁=2 В Гальванометр регулирует ток I₃=50 мА, идущий в направлении, указанном стрелкой. Определить Э.Д.С. E₂ второго элемента. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
Решение. Применим правила Кирхгофа. Выберем направления токов, как они показаны на рис.4, и условимся обходить контуры по часовой стрелке.

По первому правилу Кирхгофа для узла F имеем

I₁-I₂-I₃=0

По второму правилу Кирхгофа имеем для контура ABCDFA

-I₁r₁-I₂r₂=-E₁ ,

или после умножения обеих частей равенства на -1.

I₁r_{1 +} I₂r₂=E₁

Соответственно, для контура AFGHA

I₁r₁+I₃r₃=E₂

После подстановки числовых значений в формулы получим: I₁-I₂-0,05=0;

50I₁+25I₂=1;

100I₁+0,05·20=E₂

Перенеся в этих уравнениях неизвестные величины в левые части, а известные - в правые, получим следующую систему урав­нений:

I₁-I₂=0,05

50I₁+25I₂=1

100I₁-E₂= -1

Эту систему с тремя неизвестными можно решить обычными приемами алгебры, но так как по условию задачи требуется опре­делить только одно неизвестное E₂их трех, то воспользуемся методом определителей.

Составим и вычислим определитель системы:

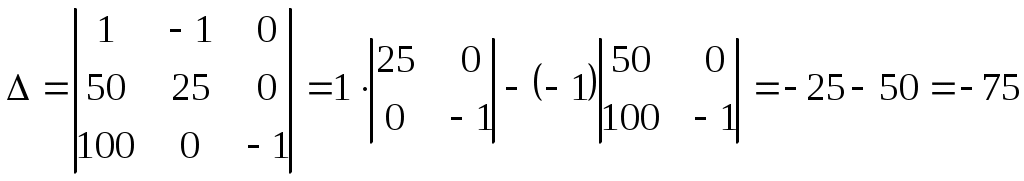Составим и вычислим определитель ΔE₂:

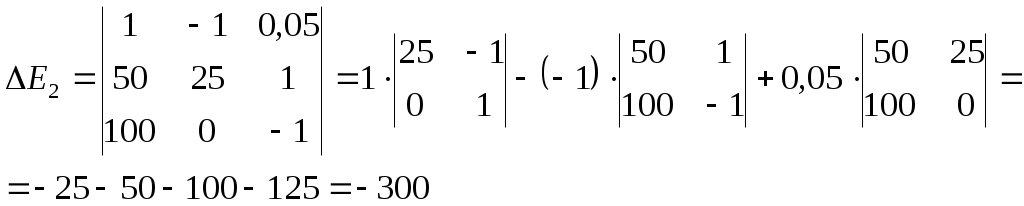Разделив определитель ΔE₂ на определитель Δ, найдем числовое значение Э.Д.С. E₂: E₂= -300 -75=4В.

Заряды.Закон Кулона.

1. 
   Какой заряд приобрел бы медный шар с радиусом 10 см, если бы удалось удалить все электроны проводимости? Плотность меди 8,9 г/см³, относительная атомная масса равна 64. Заряд электрона 1,6 10^-19 Кл, число Авогадро 6·10²³ моль^-1. Считать, что на каждый атом меди приходится один электрон проводимости.
   
2. 
   С какой силой будут притягиваться два одинаковых свинцовых шарика радиусом 1 см, расположенные на расстоянии 1 м друг от друга, если у каждого атома первого шарика отнять по одному электрону и все эти электроны перенести на второй шарик? Относительная атомная масса свинца А=207, плотность 11,3 г/см³.
   
3. 
   На двух одинаковых капельках воды находятся по одному лиш­нему электрону, причем сила электрического отталкивания капелек уравновешивает силу их взаимного тяготения. Каковы радиусы капелек?
   
4. 
   Три точечных заряда, расположенные на расстоянии 10 см друг от друга, взаимодействуют друг с другом с силами 5 Н, 8 Н, 12 Н, соответственно. Найти величину каждого из зарядов.
   
5. 
   Найти силу взаимодействия двух точечных зарядов 2 10^-7 Кл и 3 10^-7 Кл в вакууме и в керосине на расстоянии 20 см, если диэлектрическая проницаемость керосина равна 2.
   
6. 
   Два маленьких шарика обладают зарядами 2·10^-7 Кл и 4,5·10^-7 Кл и, находясь в вакууме, взаимодействуют с силой 0,1 Н. Вычислить расстояние между шариками.
   
7. 
   Два шарика, массой 1 г каждый, подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол 60°?
   
8. 
   Три точечных заряда 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
   
9. 
   Вокруг неподвижного точечного заряда +10^-9 Кл равномерно вращается под действием электростатической силы притяжения маленький шарик, заряженный отрицательно. Чему равно отношение заряда шарика к его массе, если радиус орбиты 2см, а, угловая скорость вращения 3 рад/с?
   
10. 
    Два маленьких одинаковых проводящих шарика, с зарядами q₁=-3,5·10^-9 и q₂=2,5·10^-9 Кл соединили а затем поместили нарасстоянии 5 см друг от друга. Определить заряды каждого из шариков и силу электрического взаимодействия между ними после соприкосновения.
    
11. 
    Шарик массой 2 г, имеющий заряд 2·20^-7 Кл, подвешен в воздухе на тонкой изолированной нити. Определить натяжение нити, если снизу на расстоянии 15 см расположен такой же заряд.
    
12. 
    Электрические заряды двух туч соответственно равны 20 Кл и 30 Кл. Среднее расстояние между тучами 30 км. С какой силой взаимодействуют тучи?
    
13. 
    С какой силой отталкиваются два электрона, находящиеся друг от друга на расстоянии 2·10^-8 см?
    
14. 
    Три одинаковых точечных тела с зарядами по 2 нКл находятся в вершинах равностороннего треугольника со сторонами 10 см. Определить модуль и направление силы, действующей на один из зарядов со стороны двух других.
    
15. 
    Два положительных точечных заряда Q и 9Qзакреплены на расстоянии 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
    
16. 
    Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на определенный угол. Шарики погружают в масло. Какова плотность масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков 1,5 г/см³, диэлектрическая проницаемость масла 2,2.
    
17. 
    Четыре одинаковых точечных тела с зарядами по 40 нКл каждое, закреплены в вершинах квадрата со стороной 10 см. Найти силу, действующую на одно из этих тел со стороны трех остальных.
    
18. 
    Каждый из двух шариков массой по 1г несет электрический заряд 10^-9 Кл. Во сколько раз сила электрического взаимодействия больше силы гравитационного притяжения?
    
19. 
    Два точечных заряда находятся на некотором расстоянии друг от друга. Если расстояние между ними уменьшается на 50 см, то сила взаимодействия увеличивается в два раза. Найти это расстояние.
    
20. 
    Отрицательный заряд расположен на прямой, соединяющей два одинаковых положительных точечных заряда. Расстояние между отрицательным зарядом и каждым из положительных относятся между собой как 1:3. Во сколько paз изменится сила, действующая на отрицательный заряд, если его поменять местами с ближайшим положительным.
    

---

Смотрите также файлы

• Занятие для обучающихся 3 классов по теме отчество от слова "отец".docx

• Факторы, влияющие на стабилизацию качества руд.pptx

• Ким 5 класс Входной диктант Интересная поездка.docx

• Актуализация проблемы.docx

• Лекции История буддизма Учения буддизма.pptx