Файл: Томский политехнический университет Расчетнографическая работа 1.doc

Томский политехнический университет Расчетно-графическая работа №1 Расчет разветвленной цепи постоянного тока Вариант № 985 Выполнил: студент группы 5А17 Иванов К. М. Проверил преподаватель: Колчанова В.А. Томск 2022

Условия расчетно-графических работ

ЗАДАНИЕ №1

Линейные электрические цепи с постоянными напряжениями итокамиДля заданной схемы с постоянными во времени источниками ЭДС и тока, принимаявыполнить следующее.

1. 
   Изобразить схему, достаточную для расчета токов ветвей, соединяющих узлы, помеченные буквами, указав их номера и направления.
   
2. 
   Определить токи во всех ветвях схемы и напряжение на зажимах источника тока:
   

• 
  по законам Кирхгофа,
  
• 
  методом контурных токов,
  
• 
  методом узловых потенциалов.
  

3. 
   Составить баланс вырабатываемой и потребляемой мощностей.
   
4. 
   Определить ток в ветви ab:
   

• 
  методом наложения,
  
• 
  методом преобразований.
  

5. 
   Рассматривая цепь относительно сопротивления R ветви ab как активный двухполюсник, заменить его эквивалентным генератором, определить параметры эквивалентного генератора и рассчитать ток в ветви ab, построить внешнюю характеристику эквивалентного генератора и по ней графически определить ток в ветви ab.
   
6. 
   Для любого контура без источника тока построить потенциальную диаграмму.
   
7. 
   Определить показание вольтметра.
   
8. 
   Сравнить результаты вычислений, оценить трудоемкость методов расчета и сформулировать выводы по выполненным пунктам задания.
   

Для заданной схемы дано:

---

, В;

, В;

, В;

, А.

В	В	А	град	град	град	Ом	мГн	мкФ	рад/с	мГн
190	120	3	210	60	-45	80	254.78	39.8	314

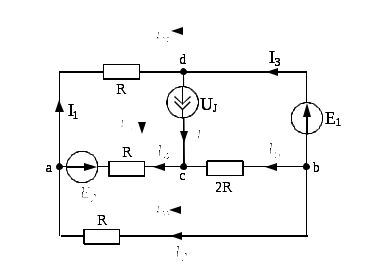
Схема:

1. 
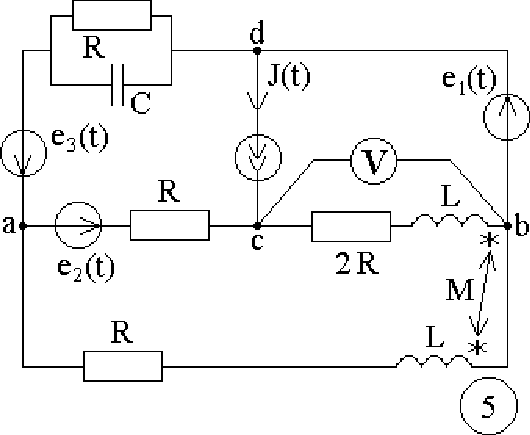
   Изображаем схему, достаточную для расчета постоянных токов ветвей, соединяющих узлы, помеченные буквами. При этом учитываем, что индуктивный элемент L для постоянного тока является “закороткой”, а емкостный элемент C при постоянном напряжении представляет собой “разрыв” ветви, причем взаимная индуктивность M влияния на постоянные токи не оказывает. Указываем произвольно номера и направления токов в ветвях схемы. Данная схема имеет: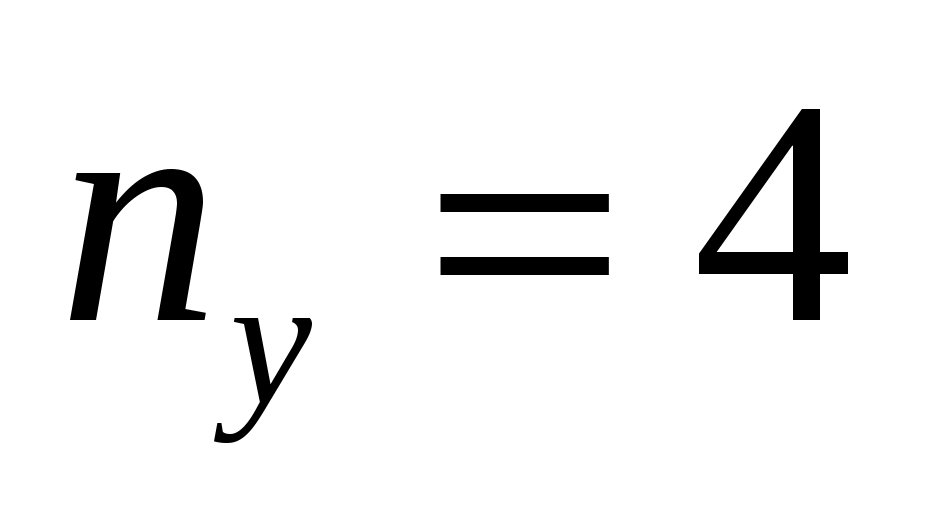 узла, 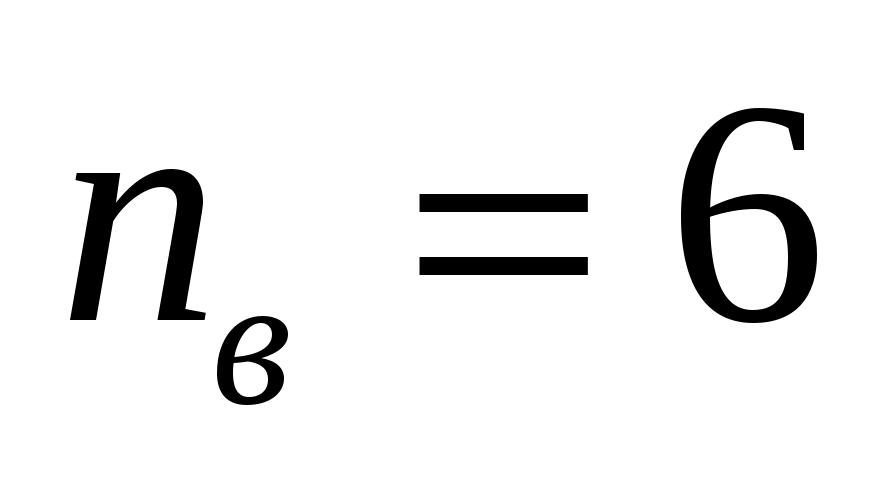ветвей, 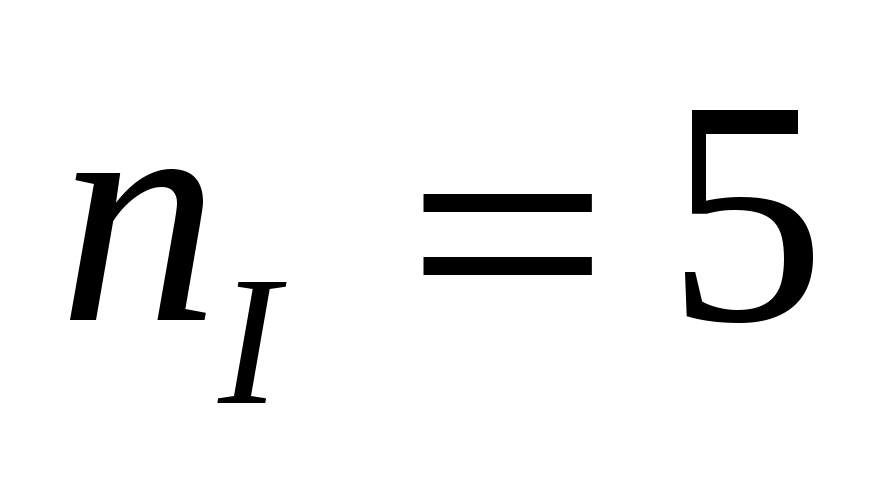неизвестных токов.
   

---

2. 
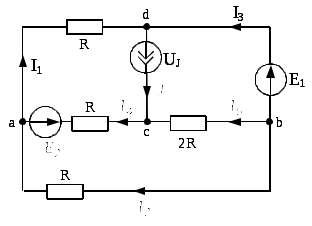
   Определяем токи во всех ветвях схемы и напряжение на зажимах источника тока.
   

1. 
   Используем законы Кирхгофа.
   

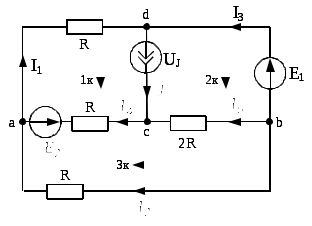
Рассчитаем число уравнений, которые необходимо составить: уравнений по первому закону Кирхгофа, уравнений по второму закону Кирхгофа.Выбираем 3 узла (например, a, b, с) и составляем уравнения по первому закону Кирхгофа:узел a: ,узел b: ,узел с: .Для трех элементарных контуров составляем уравнения по второму закону Кирхгофа1 контур: ,2 контур: ,3 контур: .Полученные 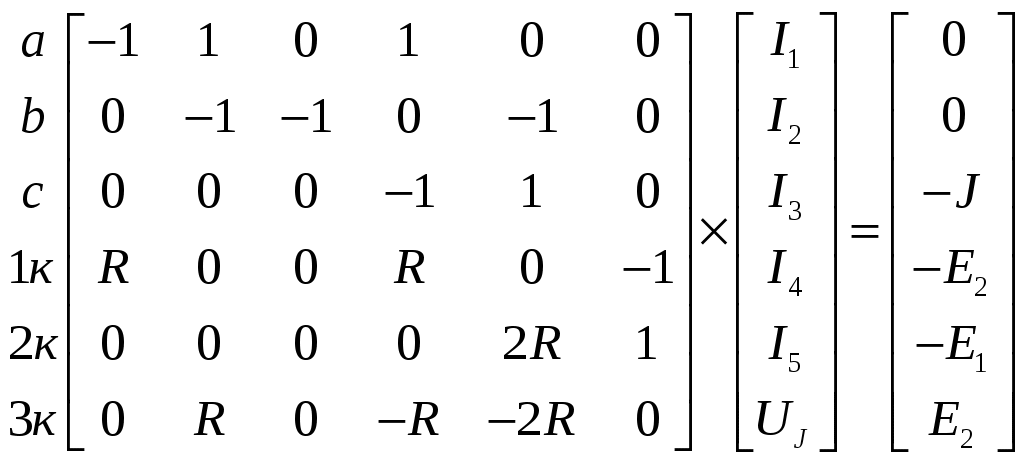уравнений записываем совместно в матричном виде т.е. или ,которые решаем на ЭВМ при помощи программы MathCad. Для этого в программу вводим матрицу коэффициентов при заданном 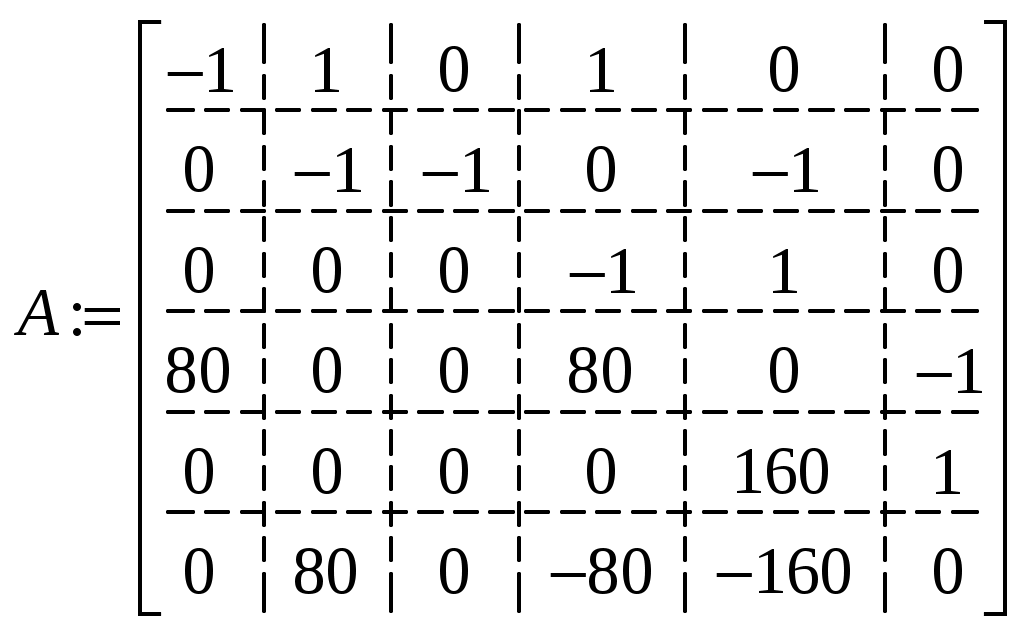 Ом: .Затем вводим в программу матрицу правой части уравнений при В; В; А:

---

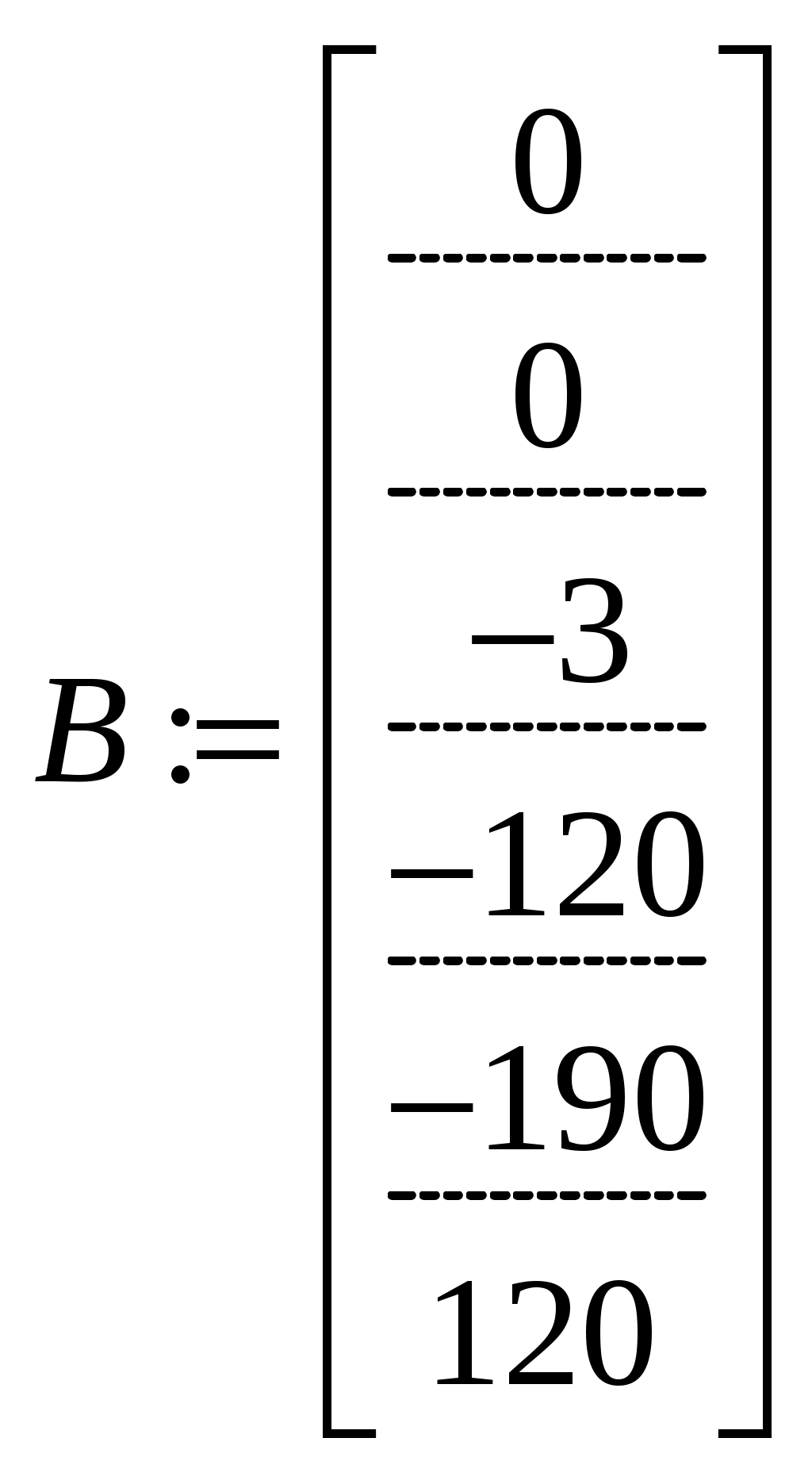.Далее вводим в программу уравнение 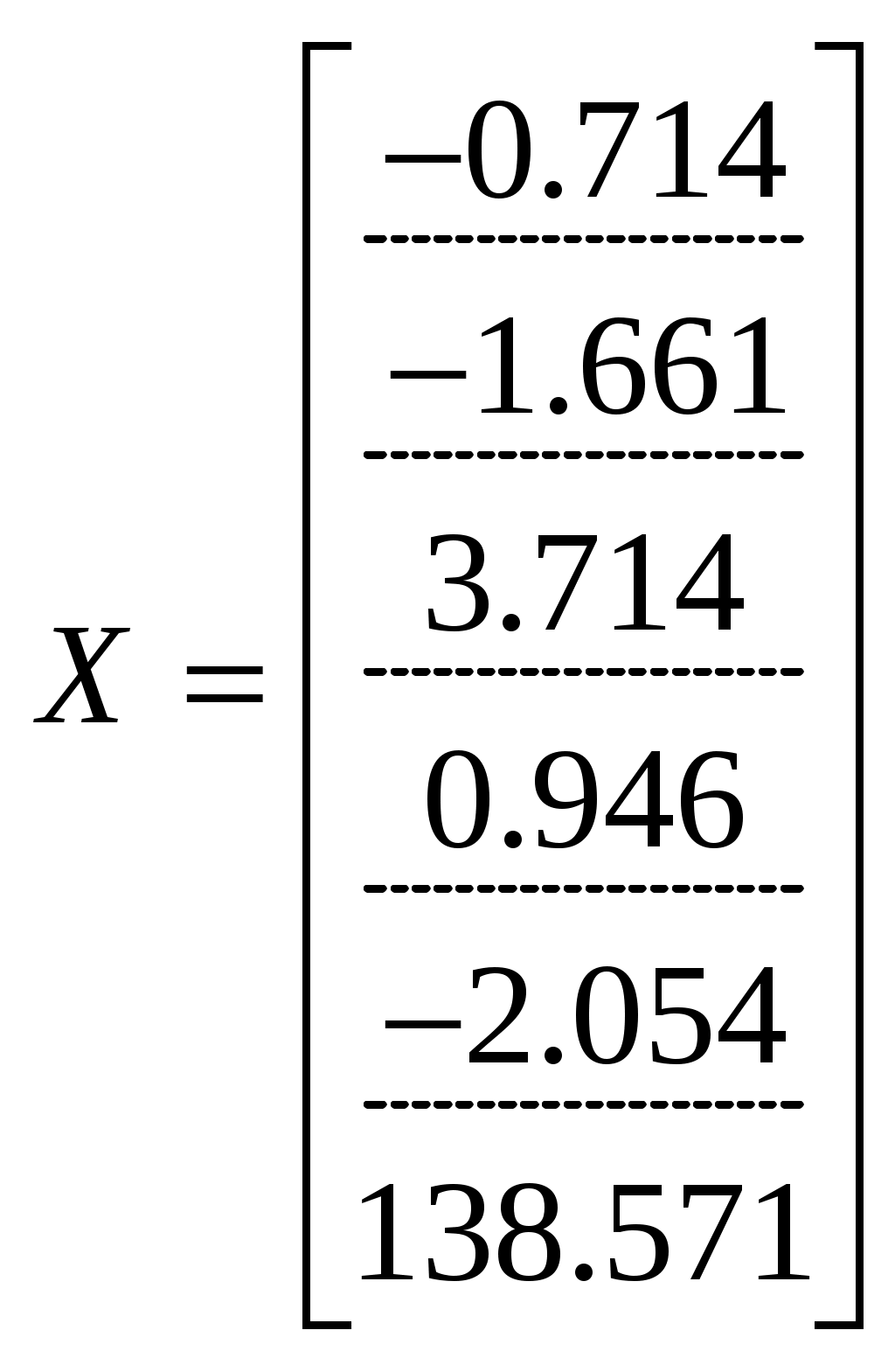и получаем решение: .Таким образом значения токов и напряжения на источнике тока получились следующие: А; А; А; А; А; В.Для предварительной проверки полученных результатов подставляем найденные токи и напряжение в одно из уравнений, составленное по первому закону Кирхгофа, и в одно уравнение, составленное по второму закону Кирхгофа.Например:a: ,3 контур: , т.е. уравнения выполняются.

2. 
   Используем метод контурных токов.
   

Рассчитываем число контурных токов, которые необходимо направить в схеме - , и число контурных уравнений, которые необходимо будет решить - .Обозначаем контурных тока как и направляем их в независимых контурах, которые отличаются друг от друга наличием хотя бы одной новой ветви, причем, через источник тока должен проходить один контурный ток, например,

---

, тогда .Для двух неизвестных контурных токов и составляем уравнениядля : ;для : .Полученные контурные уравнения можно записать в матричном виде и решить на ЭВМ при помощи программы MathCad.Получаем: А; А.Далее находим реальные токи в ветвях схемы с учетом контурных токов, проходящих в этих ветвях: А; А; А; А; А.Напряжение на зажимах источника тока найдем при помощи второго закона Кирхгофа для контура с : ,тогда В.Найденные токи в ветвях схемы и напряжение на зажимах источника тока совпадают с результатами п.2.1.

3. 
   Используем метод узловых потенциалов.
   

---