Файл: Томский политехнический университет Расчетнографическая работа 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Потенциал одного из узлов принимаем равным нулю. Таким узлом будет один из узлов ветви без сопротивления, например,
Для неизвестных потенциалов
для
для
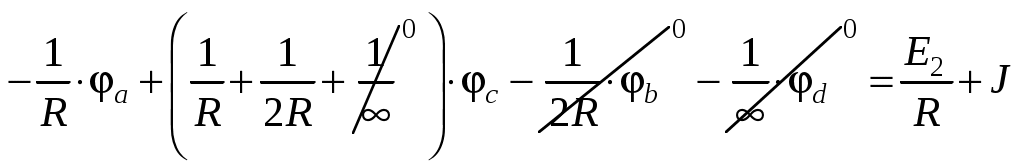 ;
;Полученные уравнения можно записать в матричном виде (
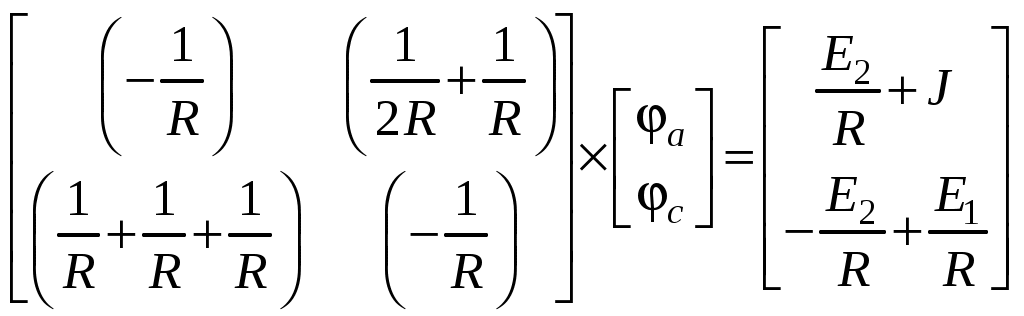
Получаем:
Далее используем обобщенный закон Ома и первый закон Кирхгофа:
Таким образом, найденные токи и напряжение на зажимах источника тока совпадают с результатами п.2.1. и п.2.2.
-
Для проверки правильности расчетов составляем баланс вырабатываемой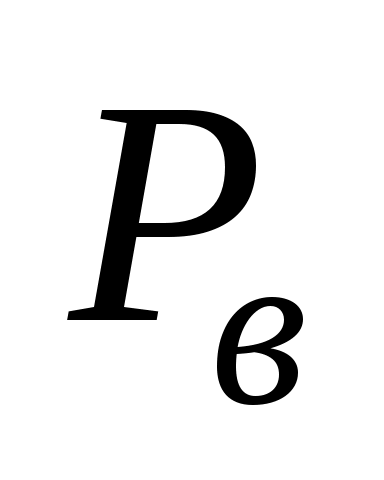 и потребляемой
и потребляемой 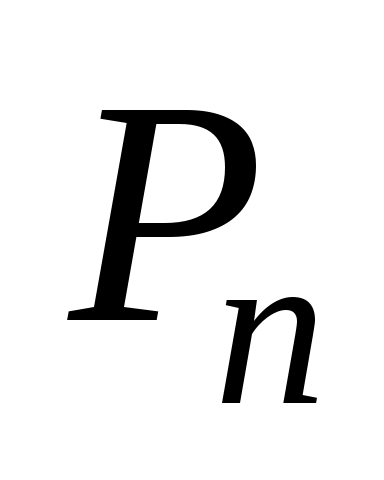 мощности:
мощности:
Таким образом, получаем допустимую относительную погрешность расчетов
-
Определяем ток в ветви ab тремя методами.
-
Используем метод наложения.
Для расчета тока
-
Расчет подсхемы с ЭДС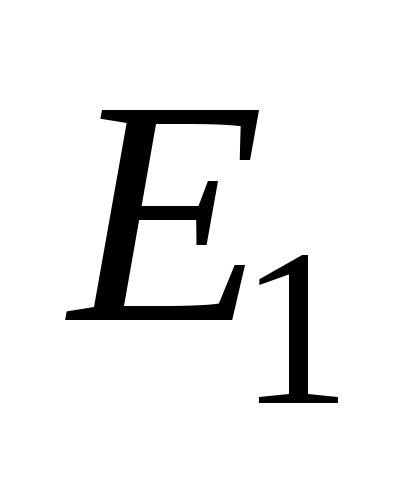 .
.
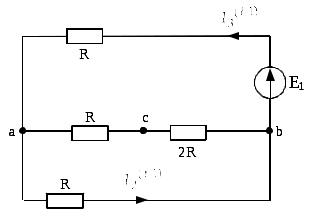
По закону Ома:
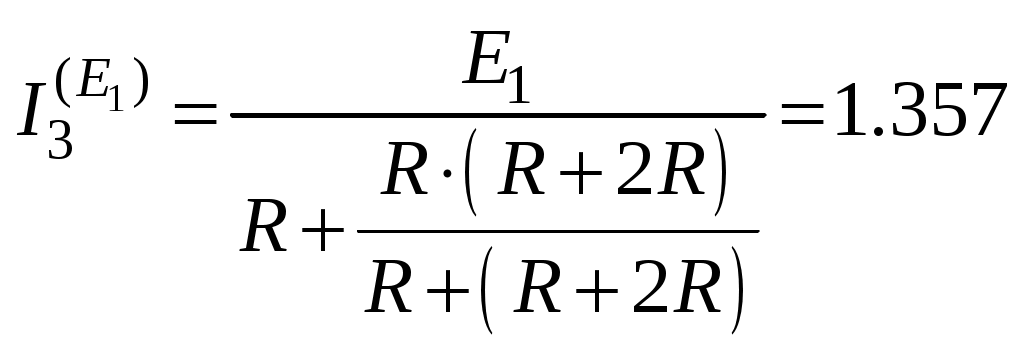 А, тогда по правилу разброса находим частичный искомый ток, создаваемый ЭДС
А, тогда по правилу разброса находим частичный искомый ток, создаваемый ЭДС -
Расчет подсхемы с ЭДС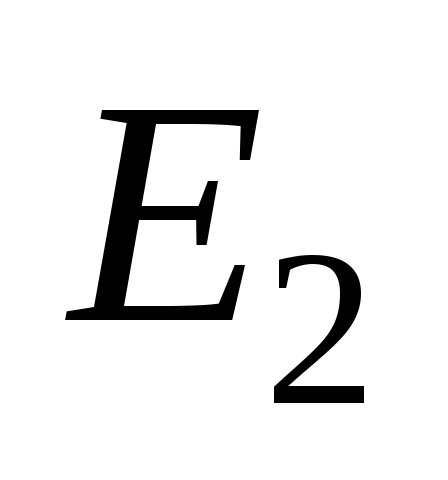 .
.
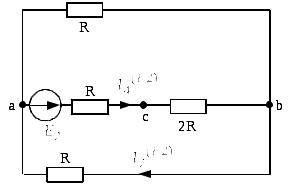
По закону Ома:
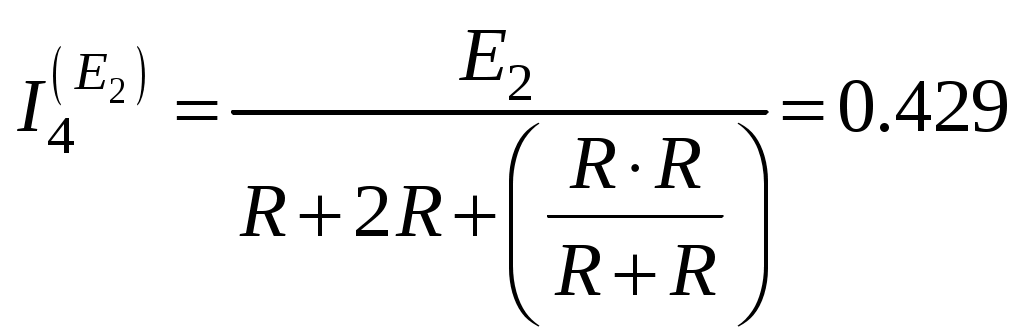 А. тогда по правилу разброса находим частичный искомый ток, создаваемый ЭДС
А. тогда по правилу разброса находим частичный искомый ток, создаваемый ЭДС -
Расчет подсхемы с источником тока .
.
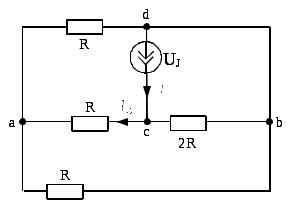
Преобразуем схему объединив узлы bиd:
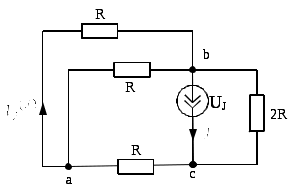
Преобразуем схему ещё раз и найдём ток
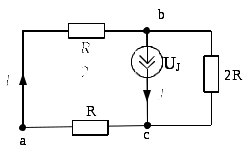
По правилу разброса находим ток
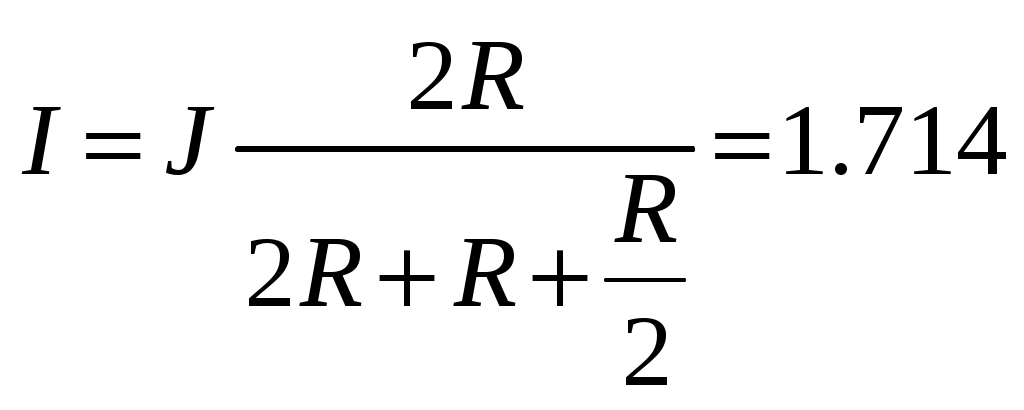 А.
А. Тогда ток
Находим результирующий ток
Рассчитанный ток
-
Используем метод преобразований.
Для расчета тока
Для этого преобразования проведем в несколько этапов. Вначале перенесём ЭДС E1 через узел d на ветвь ad и преобразуем схему:

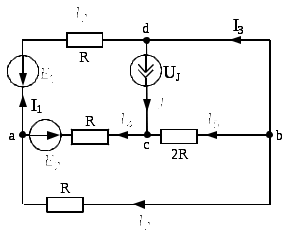
Затем преобразуем источник тока в ЭДС
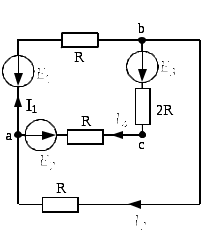
Далее преобразуем ветвь acb. Найдём общее сопротивление и общее ЭДС в этой ветви:
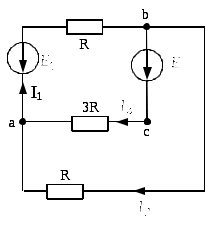
Далее преобразуем параллельное соединение источников ЭДС и сопротивления ветвей
ab и acb:
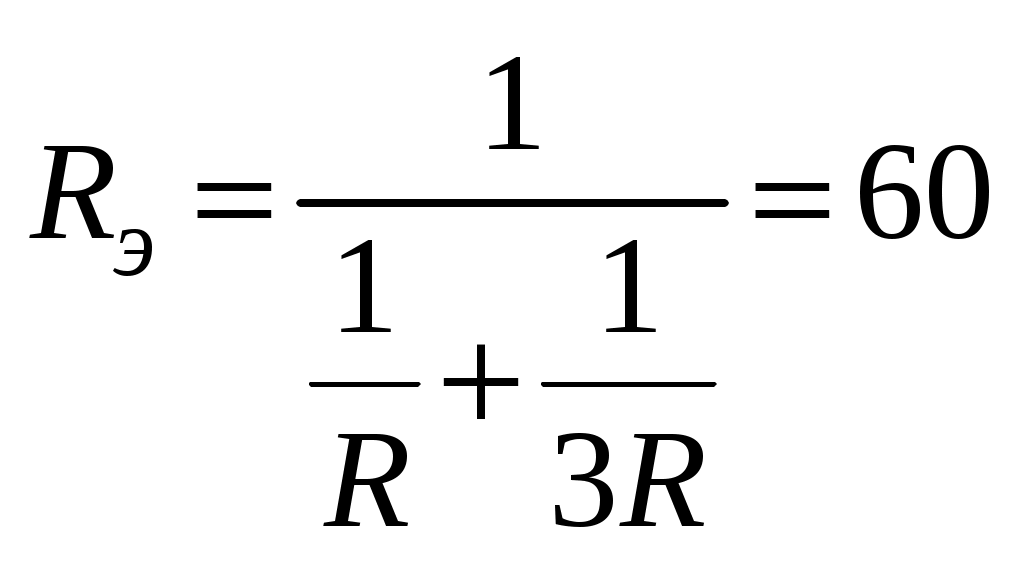 Ом;
Ом; В результате получаем одноконтурную схему с искомым током
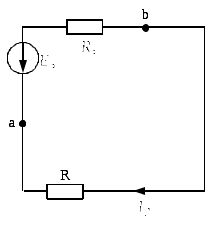
Тогда по закону Ома:
Найденный ток
-
Определяем ток в ветви ab методом эквивалентного генератора.-
Находим собственное сопротивление цепи ветви ab:
-
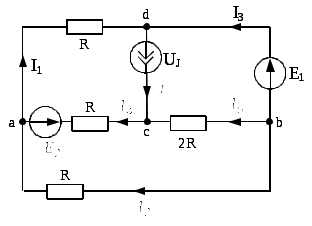
-
Находим сопротивление эквивалентного генератора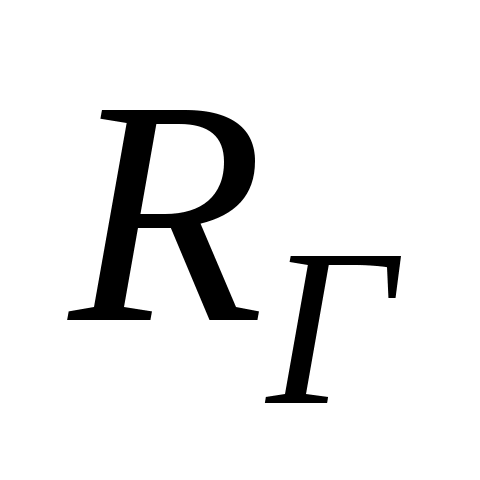 :
:
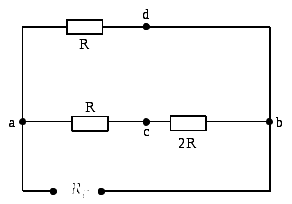
-
Находим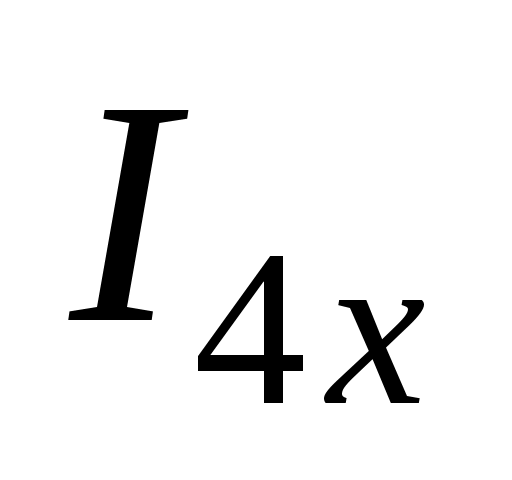 и
и 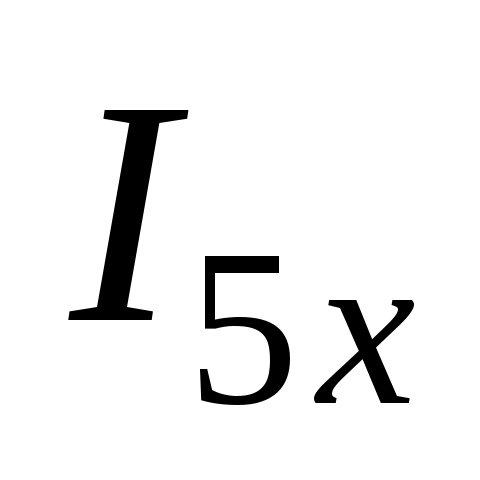 с помощью метода контурных токов:
с помощью метода контурных токов:
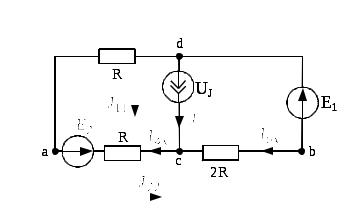
Тогда:
-
Находим напряжение эквивалентного генератора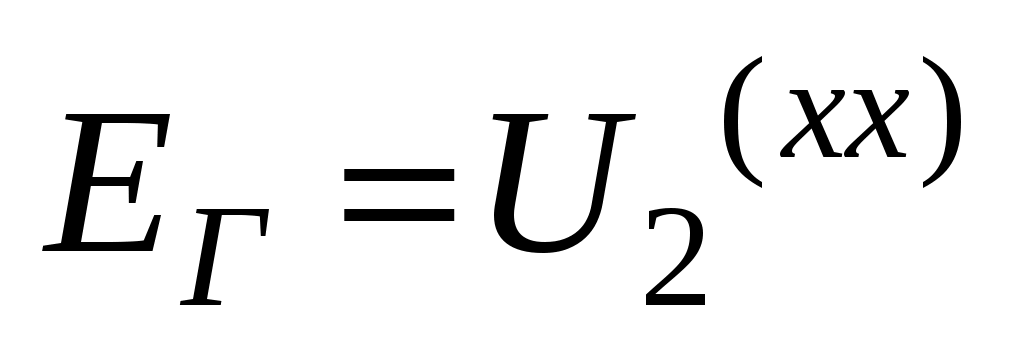 и ток эквивалентного генератора
и ток эквивалентного генератора 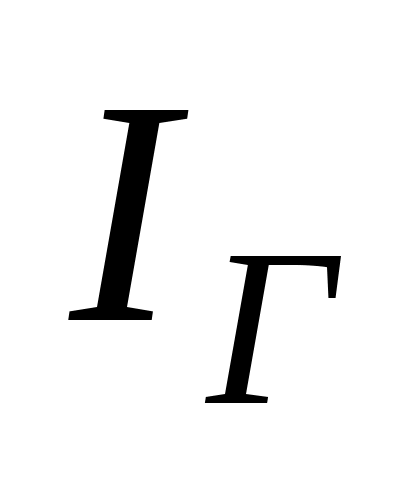 :
:
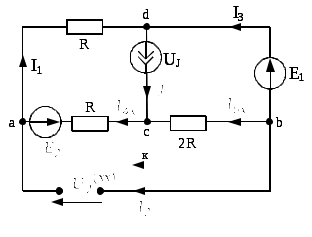
Для этого запишем 2 закон Кирхгофа для контура
к:
Тогда
-
Находим ток в ветви ab аналитически по двум формулам:
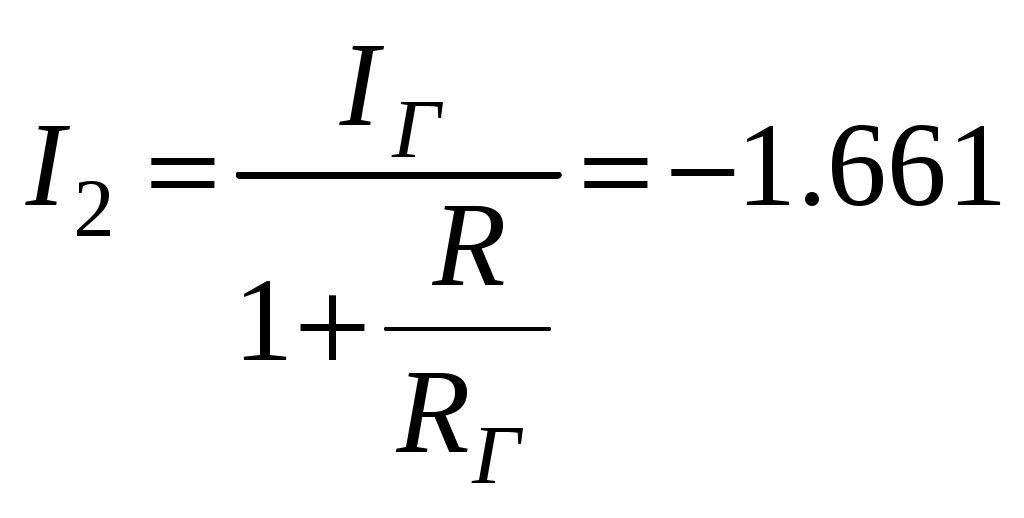 А.
А.-
Находим ток в ветви ab графически:
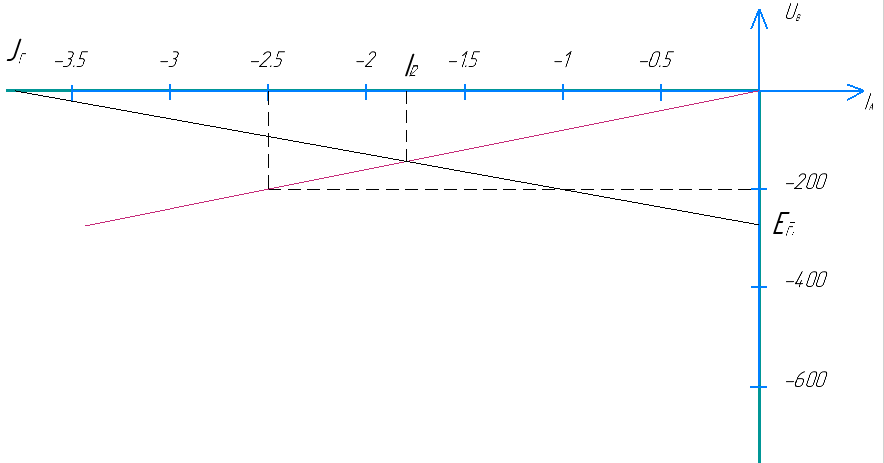
Точка пересечения внешней ВАХ эквивалентного генератора с ВАХ резистора
Аналитический и графический расчет методом эквивалентного генератора позволяет найти ток
-
Для контура без источника тока, например, bcab строим потенциальную диаграмму. При этом обозначаем промежуточную точку k и принимаем потенциал точки b, как и в методе узловых потенциалов, равным нулю, т.е. .
.
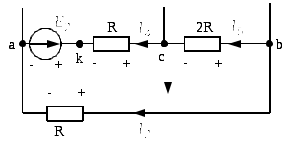
Тогда при принятом обходе выбранного контура по часовой стрелке, проводим расчет потенциалов точек:
т.е. расчеты проведены верно, т.к. получилось