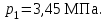Добавлен: 11.12.2023
Просмотров: 45
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача № 1.4
Условие:
Определить абсолютное давление в сосуде по показанию жидкостного манометра, если известно: h1 = 2 м; h2 = 0,5 м; h3 = 0,2 м; ρм = 880 кг/м³.
Решение:
Дано:
| h1 = 2 м |  |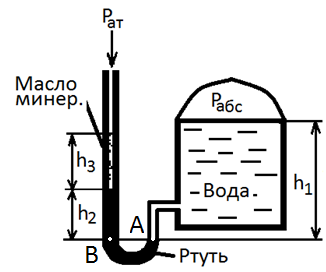
| h2 = 0,5 м | |
| h3 = 0,2 м | |
| ρм = 880 кг/м³ | |
| ρрт = 13600 кг/м3 | |
| ρв = 1000 кг/м3 | |
| Найти: pабс - ? |
Давление в точках А и В равно, так как они лежат в одной горизонтальной плоскости, проходящей в однородной жидкости, поэтому:
pат + ρм * g * h3 + ρрт * g * h2 = pабс + ρв * g * h1.
Тогда абсолютное давление в сосуде:
pабс = pат + ρм * g * h3 + ρрт * g * h2 – ρв * g * h1 =
= 100000 + 880 * 9,81 * 0,2 + 13600 * 9,81 * 0,5 – 1000 * 9,81 * 2 =
= 148815 Па = 148 кПа.
Ответ: pабс = 148 кПа.
Задача № 2.5
Условие:
Цилиндрический сосуд с размерами D = 2,3 м и L = 5 м заполнен бензином. Определить разрывающие усилия Fx, если показания манометра рм = 58 кПа.
Решение:
Дано:
| D = 2,3 м |  |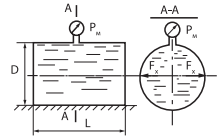
| L = 5 м | |
| рм = 58 кПа | |
| ρ = 800 кг/м³ | |
| Найти: Fx - ? |
Сила, разрывающая цистерну, равна горизонтальной составляющей силы давления воды на криволинейную стенку:
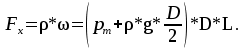
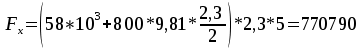Н.Ответ: Fx = 770,8 кН.
Задача № 3.4
Условие:
Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте Н = 2 м и постоянное давление Р = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d1 = 75 мм, показывает Р1 = 0,25 МПа. Определить расход жидкости Q,
если диаметр искривленной трубы, подводящей жидкость к баку, равен d2 = 50 мм; коэффициент сопротивления этой трубы принят равным ζ = 0,5. Плотность жидкости ρ = 800 кг/м³.
Решение:
Дано:
| Н = 2 м |   |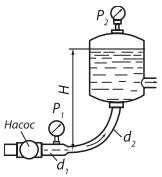
| Р = 0,2 МПа | |
| d1 = 75 мм | |
| Р1 = 0,25 МПа | |
| d2 = 50 мм | |
| ζ = 0,5 | |
| ρ = 800 кг/м³ | |
| Найти: Q - ? |
Для решения данной задачи нужно использовать уравнение Бернулли, записав его для двух сечений: сечение 1-1 — в месте подсоединения манометра к трубопроводу с диаметром d1 , сечение 2-2 — по свободной поверхности жидкости в баке, плоскость сравнения 0-0 — по осевой линии горизонтальной части трубы, т.к. относительно ее дано расстояние Н до свободной поверхности жидкости. Для выбранных сечений и плоскости сравнения уравнение Бернулли запишется следующим образом:
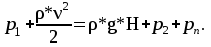
Последнее слагаемое в правой части уравнения, потери давления рп , можно записать как:
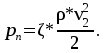
Скорости v1 и v2 можно выразить через расход и сечение труб, т.е.:
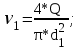
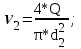
С учетом полученных выражений уравнение Бернулли будет иметь вид:
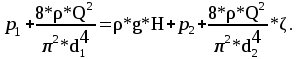
Перегруппировав члены уравнения и вынеся общие множители за скобки, получим следующее уравнение:
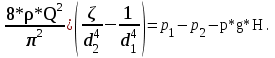
Из последнего уравнения получим:
Q =
=
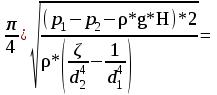
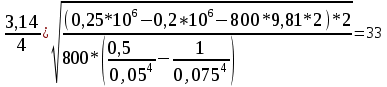л/с.
Ответ: Q = 33 л/c.
Задача № 4.5
Условие:
Какое избыточное давление рм воздуха нужно поддерживать в баке, чтобы его опорожнение происходило в два раза быстрее, чем при атмосферном давлении над уровнем воды; каким будет при этом время опорожнения бака? Диаметр бака D = 0,9 м, его начальное заполнение Н = 2,1 м. Истечение происходит через цилиндрический насадок диаметром d = 30 мм, коэффициент расхода которого μ = 0,82.
Решение:
Дано:
| D = 0,9 м |  |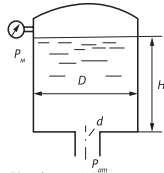
| Н = 2,1 м | |
| d = 30 мм | |
| μ = 0,82 | |
| Найти: рм - ? t - ? |
Запишем уравнение Бернулли для движения жидкости от свободной поверхности до выхода в атмосферу:
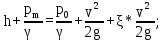
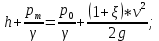
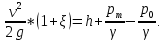
Скорость истечения жидкости из отверстия:
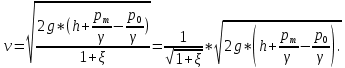
Коэффициент скорости:
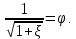
Коэффициент расхода:
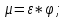
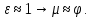
Скорость истечения жидкости из отверстия:
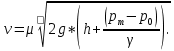
Расход через отверстие:
.
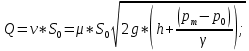
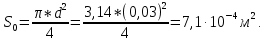
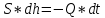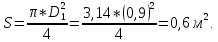
Равенство расходов через свободную поверхность и отверстие:
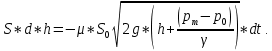
Время истечения жидкости из закрытого сосуда:
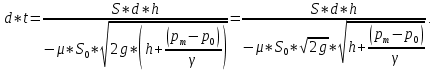
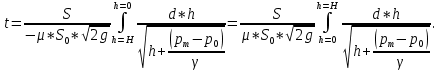
Если сосуд открыт, то время истечения жидкости:
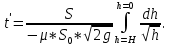
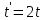(по условии задачи).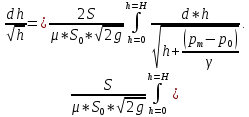
Сократим левую и правую часть на:
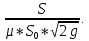
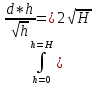
Найдем интеграл:
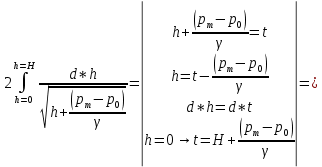
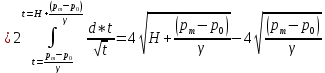
Следовательно:
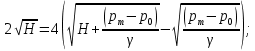
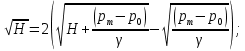
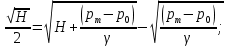
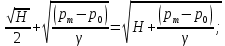
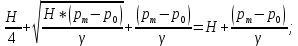
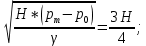
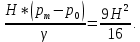
Избыточное давление в баке:
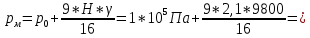
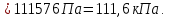
Время опорожнения сосуда:
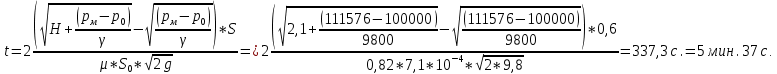
Ответ: pм = 111,6 кПа; t = 5 мин. 37 с.
Задача № 5.4
Условие:
Какое давление должен создавать насос при подаче масла Q = 0,4 л/с и при давлении воздуха в пневмогидравлическом аккумуляторе р2 = 2 МПа, если коэффициент сопротивления квадратичного дросселя ξ = 100; длина трубопровода от насоса до аккумулятора l = 4 м; диаметр d = 10 мм? Свойства масла ρ = 900 кг/м3; ν = 0,5 Ст. Коэффициент ξ отнесен к трубе d = 10 мм.
Решение:
Дано:
| Q = 0,4 л/с |  |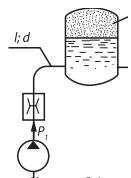
| р2 = 2 МПа | |
| ξ = 100 | |
| l = 4 м | |
| d = 10 мм | |
| ρ = 900 кг/м3 | |
| ν = 0,5 Ст | |
| Найти: р1 - ? |
Определим режим течения жидкости:
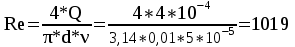(ламинарный).Запишем уравнение Бернулли для сечений 1-2:
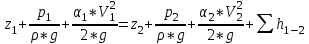, где
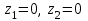— положения соответствующих сечений относительно плоскости сравнения; 
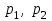— избыточные давления в соответствующих сечениях; 
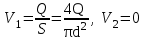— скорости истечения жидкости; 
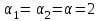— коэффициенты Кориолиса для ламинарного течения; 
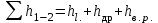— суммарные потери напора (потери по длине, в дросселе и на внезапном расширении); 
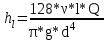– потери напора по длине; 
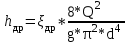– потери на дросселе; 
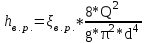— потери на внезапном расширении, 
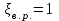.Таким образом, получаем:
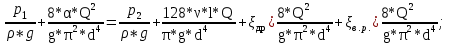
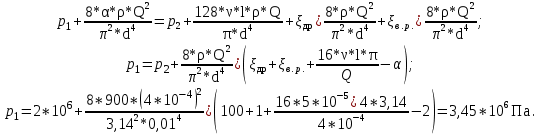
Ответ:
