Пример 15. Фирма производит детские платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение августа – сентября на единицу продукции составили: платья – 7 ден. ед., костюма – 28 ден. ед. Цена реализации составляет 15 и 50 ден. ед., соответственно.

По данным наблюдений за несколько предыдущих лет, фирма может реализовать в условиях теплой погоды 1950 платьев и 610 костюмов, а при прохладной погоде 630 платьев и 1050 костюмов.

В связи с возможными изменениями погоды определим стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход от реализации продукции. Задачу решим с использованием критериев природы, приняв λ = 0,5.

▲ Фирма располагает двумя стратегиями:

• А₁ – в этом году будет теплая погода;

• А₂ – погода будет прохладная.

Возможные состояния природы:

• В₁– будет теплая погода;

• В₂ – будет прохладная погода.

Доход фирмы (ден. ед.) составит:

• при выборе стратегии А₁ и состоянии погоды В₁

1950∙(15 -7) + 610∙(50 - 28) = 29020;

• при выборе стратегии А₁ и состоянии погоды В₂

630∙(15 - 7) + 610∙(50 - 28) - 7∙(1950 - 630) = 9220;

• при выборе стратегии А₂ и состоянии погоды В₁

630∙(15 - 7) + 610∙(50 - 28) - 28∙(1050 - 610) = 6140;

• при выборе стратегии А₂ и состоянии погоды В₂

630∙(15 - 7) + 1050∙(50 - 28) = 28140.

Рассматривая фирму и погоду в качестве двух игроков, запишем платежную матрицу со столбцами M_i, α_i, ω_i, γ_i.

	В1	В2	Mi	αi	ωi	γi
А1 А2	29020 6140	9220 28140	19120* 17140	9220* 6140	29020* 28140	19120* 17140

Рассмотрим использование различных критериев природы.

Критерий Лапласа: max M_i = 19120, т.е. фирме целесообразно использовать стратегию А₁.

Критерий Вальда:

---

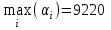
, т.е. фирме целесообразно использовать стратегию А₁.

Критерий максимума: 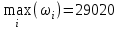, т.е. фирме целесообразно использовать стратегию А₁.

Критерий Гурвица: 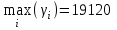, т.е. фирме целесообразно использовать стратегию А₁.

Критерий Сэвиджа. Запишем матрицу риска r_ij со столбцом δ_i:

	В1	В2	δi
А1 А2	0 22880	18920 0	18920* 22880

Так как min δ_i = 18920, то фирме целесообразно использовать стратегию А₁.

Оптимальной по всем критериям является стратегия А₁.

Таким образом, фирме целесообразно производить 1950 платьев и 610 костюмов, тогда при любой погоде она получит доход не менее 9220 д. ед.▲

Принятие решений в условиях риска

Математическая модель задачи принятия решений в условиях риска предполагает задание дополнительной информации о поведении «природы» в виде вероятностей ее различных состояний.

Когда состояниям природы поставлены в соответствие вероятности, заданные экспертно либо вычисленные, решение обычно принимается на основе критерия максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска.

Если для некоторой игры с природой, задаваемой платежной матрицей (a_ij)_mn, стратегиям природы П соответствует вектор вероятности p = (p₁, p₂,…, p_n) состояний среды, то лучшей стратегией игрока А будет та, которая обеспечит ему максимальный средний выигрыш, т.е.



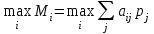
Применительно к матрице рисков лучшей будет та стратегия игрока, которая обеспечивает ему минимальный средний риск, т.е.



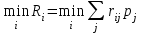
Эти критерии эквивалентны в том смысле, что оптимальные значения для них обеспечивает одна и та же стратегия игрока

---

А.

Пример 16. Пусть платежная матрица и вероятности состояния среды представлены таблицей

Стратегия игрока A	Вероятность различных состояний среды				Mi
	0,4	0,2	0,2	0,2
А1 А2 А3 А4	5 2 8 1	2 3 5 4	8 4 3 2	4 12 10 8		4,8 4,6 6,8 3,2

▼ В столбце M_iтаблицы указаны .

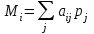Поскольку 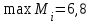, то А₃ – лучшая стратегия игрока А.

Матрица риска, соответствующая искомой платежной матрице:

Стратегия игрока A	Вероятность различных состояний среды				Ri
	0,4	0,2	0,2	0,2
А1 А2 А3 А4	3 6 0 7	3 2 0 1	0 4 5 6	8 0 2 4	3,4 3,6 1,4 5

В столбце R_iтаблицы указаны .

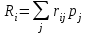Поскольку 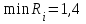, то А₃ – лучшая стратегия игрока А▲
Дерево решений

Рассмотренные нами критерии принятия решений позволяют делать вывод из совокупности так называемых одноэтапных альтернатив. При этом подразумевается, что решения, принимаемые в будущем, не зависят от решений, принимаемых в текущий момент.

Рассмотрим многоэтапный процесс принятия решений, в котором взаимозависимые решения принимаются последовательно. Графически подобные процессы могут быть представлены с помощью дерева решений. Такое представление облегчает описание процесса принятия решений.

---

Дерево решений – это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности и выигрыш для любых комбинаций альтернатив и состояний среды.

Дерево решений состоит из ряда узлов (квадраты, круги) и исходящих из них ветвей (линий). Рисуют деревья слева направо.

При формировании дерева используются следующие обозначения: квадраты - места принятия решений; круги - места появления исходов; пунктирные линии - возможные решения; сплошные линии - возможные исходы.

Ожидаемая денежная оценка (ОДО) – это средний выигрыш в игре, он рассчитывается как сумма произведений размеров выигрышей на вероятности этих выигрышей.

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок (ОДО), отбрасыванием неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО.

Пример. Предприятие решает вопрос, какую назначить цену на свой товар: 40 руб. или 50 руб. Если будет установлена цена 40 руб., то возможны следующие варианты объема продаж: 40000 руб. с вероятностью 0,2; 35000 руб. с вероятностью 0

---

Смотрите также файлы

• !Сйытар мен газдарды озалысы туралы ылымгидромеханика задарымен жылдамдыты анытайтын процестер.docx

• Материал в учебнике 17. История чисел и систем счисления.doc

• Тесты по курсу "Экономика общественного сектора" Концепция "экономического человека".docx

• Содержание Введение Глава Теоретические аспекты изучения советских комплексных систем управления качеством система сбт Понятие о сбт Принцип работы сбт введение.docx

• Учебник ответственные редакторы доктор юридических наук, профессор Ю. В. Грачева, доктор юридических наук, профессор.doc