ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 199
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3 – через y1, y2, y3.
Для первого игрока (торговой фирмы) математическая модель задачи имеет вид
при ограничениях
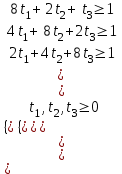
Решаем задачу в Excel (Поиск решения)
Оптимальное решение:
t = (0,1020; 0,0561; 0,0714), Fmin=0,2296,
тогда цена игры
v* = 1/Fmin = 1/0,2296 = 4,355,
и оптимальное решение
x* = tv* = (0,1020; 0,0561; 0,0714)·4,355 = (0,444; 0,244; 0,311).
Таким образом, торговая фирма на ярмарке должна придерживаться стратегии х* = (0,444; 0,244; 0,311), при этом она получит доход не менее v* = 4,355 ден. ед.
Для второго игрока (конъюнктуры рынка и спроса покупателей) математическая модель задачи имеет вид:
при ограничениях
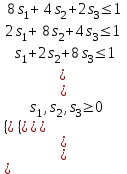
Решаем задачу в Excel (Поиск решения)
Оптимальное решение:
s = (0,0714; 0,0561; 0,1020), Gmax=0,2296,
тогда цена игры
v* = 1/Gmax = 1/0,2296 = 4,355,
и оптимальное решение
y* = sv* = (0,0714; 0,0561; 0,1020)·4,355 = (0,314; 0,244; 0,444),
при этом v* = 4,355 - расходы покупателей. ▲
Упражнение 7. Предприятием разработан ряд хозяйственных стратегий по продаже товаров А1, А2, А3 (стратегии предприятия) с учетом трех вариантов поведения покупателей В1, В2, В3 (стратегии покупателей). Платежная матрица представляет собой оценки прибыли (млн. руб).
Найти оптимальную стратегию игрока А (предприятие) и игрока В (покупатели).
Ответ:
Оптимальное решение для игрока А (предприятие)
x* = (0,818; 0; 0,182),
при этом v* = 8,182 – доход предприятия.
Оптимальное решение для игрока В (покупателя)
y* = (0,909; 0; 0,091),
при этом v* = 8,182 – расходы покупателей ▲
Игры с природой
В некоторых ситуациях лицу, принимающему решение, противостоит не разумный противник, а природа, которая действует случайно.
Принятие решений в условиях полной неопределенности
Пример 14. Пусть рассматривается игра с природой с четырьмя стратегиями игрока Аи тремя состояниями природы П. Матрица выигрышей задана таблицей
Если данных о вероятностях состояний среды (природы) не имеется, то лицо, принимающее решения (ЛПР), находится в условиях неопределенности.
Основной метод, позволяющий найти оптимальное решение в условиях неопределенности, состоит в формулировке некоторой гипотезы о поведении среды, позволяющей дать каждому альтернативному решению числовую оценку.
Рассмотрим некоторые критерии, используемые при выборе оптимальной стратегии игрока А в условиях неопределенности.
1. Критерий Бейеса – Лапласа. В качестве оптимальной выбирается та стратегия, которая дает максимум математического ожидания выигрыша, т.е.
,
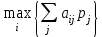где рj– вероятность реализации состояния Пj.
Поскольку в нашем примере вероятности неизвестны, то предполагается равновероятность состояний природы (критерий Лапласа).
В столбце Мi таблицы указаны средние арифметические
.
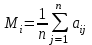Из величин Mi максимальное значение равно 45, следовательно, оптимальной является стратегия А4.
2. Максиминный критерий Вальда (критерий пессимиста). В качестве оптимальной выбирается та стратегия, при которой минимальный выигрыш максимален, т.е.
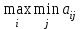
Критерий является пессимистическим, поскольку считается, что природа будет действовать наихудшим образом для человека.
В столбце αi таблицы указаны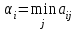
. Из величин αi максимальная величина есть 25, следовательно, оптимальной является стратегия А3.
3. Критерий максимума (критерий оптимиста). В качестве оптимальной выбирается та стратегия, при которой максимальный выигрыш максимален, т.е.
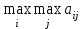
Критерий является оптимистическим, поскольку считается, что природа будет наиболее благоприятна для человека.
В столбце ωi таблицы указаны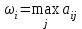
. Из величин ωi максимальная равна 85, следовательно, оптимальной является стратегия А4.
4. Критерий Гурвица. В качестве оптимальной выбирается та стратегия, при которой максимально линейная комбинация минимального и максимального выигрышей, т.е.
,
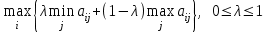где λ – показатель пессимизма.
Если λ =1, критерий Гурвица превращается в пессимистический критерий Вальда, а при λ = 0 – в критерий крайнего оптимизма. Обычно показатель λ принимается в пределах от 0,5 до 0,7. Пусть λ = 0,6.
В столбце γi таблицы указаны γi = 0,6 αi+ 0,4 ωi. Из величин γi максимальная равна 47, следовательно, оптимальной является стратегия А3.
5. Критерий Сэвиджа (критерий сожалеющего пессимиста). В качестве оптимальной выбирается та стратегия, при которой минимален максимальный риск, т.е.
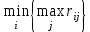
Риском называют разность между выигрышем, который можно получить, если знать действительное состояние природы, и выигрышем, который будет получен при отсутствии этой информации, т.е.
.
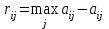Матрица риска будет иметь в нашем случае следующий вид:
В столбце δi построенной матрицы риска указаны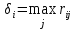
. Из величин δi минимальная равна 60, следовательно, оптимальной является любая из стратегий А2, А3.
Каждый из рассмотренных критериев не может быть признан вполне удовлетворительным для окончательного выбора решений, однако их совместный анализ позволяет более наглядно представить последствия принятия тех или иных управленческих решений.
Для первого игрока (торговой фирмы) математическая модель задачи имеет вид
при ограничениях
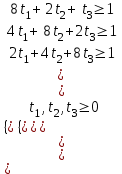
Решаем задачу в Excel (Поиск решения)
| | t1 | t2 | t3 | | |
| | 0,1020 | 0,0561 | 0,0714 | | |
| F | 1 | 1 | 1 | 0,2296 | |
| B1 | 8 | 2 | 1 | 1 | 1 |
| B2 | 4 | 8 | 2 | 1 | 1 |
| B3 | 2 | 4 | 8 | 1 | 1 |
Оптимальное решение:
t = (0,1020; 0,0561; 0,0714), Fmin=0,2296,
тогда цена игры
v* = 1/Fmin = 1/0,2296 = 4,355,
и оптимальное решение
x* = tv* = (0,1020; 0,0561; 0,0714)·4,355 = (0,444; 0,244; 0,311).
Таким образом, торговая фирма на ярмарке должна придерживаться стратегии х* = (0,444; 0,244; 0,311), при этом она получит доход не менее v* = 4,355 ден. ед.
Для второго игрока (конъюнктуры рынка и спроса покупателей) математическая модель задачи имеет вид:
при ограничениях
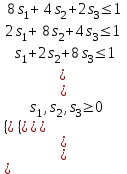
Решаем задачу в Excel (Поиск решения)
| | s1 | s2 | s3 | | |
| | 0,0714 | 0,0561 | 0,1020 | | |
| F | 1 | 1 | 1 | 0,2296 | |
| А1 | 8 | 4 | 2 | 1 | 1 |
| А2 | 2 | 8 | 4 | 1 | 1 |
| А3 | 1 | 2 | 8 | 1 | 1 |
Оптимальное решение:
s = (0,0714; 0,0561; 0,1020), Gmax=0,2296,
тогда цена игры
v* = 1/Gmax = 1/0,2296 = 4,355,
и оптимальное решение
y* = sv* = (0,0714; 0,0561; 0,1020)·4,355 = (0,314; 0,244; 0,444),
при этом v* = 4,355 - расходы покупателей. ▲
Упражнение 7. Предприятием разработан ряд хозяйственных стратегий по продаже товаров А1, А2, А3 (стратегии предприятия) с учетом трех вариантов поведения покупателей В1, В2, В3 (стратегии покупателей). Платежная матрица представляет собой оценки прибыли (млн. руб).
| План продаж | Прибыль | αi | ||
| В1 | В2 | В3 | ||
| А1 А2 А3 | 8 4 9 | 13 10 6 | 10 2 0 | 8 2 0 |
| βj | 9 | 13 | 10 | |
Найти оптимальную стратегию игрока А (предприятие) и игрока В (покупатели).
Ответ:
Оптимальное решение для игрока А (предприятие)
x* = (0,818; 0; 0,182),
при этом v* = 8,182 – доход предприятия.
Оптимальное решение для игрока В (покупателя)
y* = (0,909; 0; 0,091),
при этом v* = 8,182 – расходы покупателей ▲
Игры с природой
В некоторых ситуациях лицу, принимающему решение, противостоит не разумный противник, а природа, которая действует случайно.
Принятие решений в условиях полной неопределенности
Пример 14. Пусть рассматривается игра с природой с четырьмя стратегиями игрока Аи тремя состояниями природы П. Матрица выигрышей задана таблицей
| Матрица выигрышей | Расчетные показатели | ||||||
| | П1 | П2 | П3 | Mi | αi | ωi | γi |
| А1 А2 А3 А4 | 20 75 25 85 | 30 20 80 5 | 15 35 25 45 | 21,7 43,3 43,3 45* | 15 20 25* 5 | 30 75 80 85* | 21 42 47* 37 |
Если данных о вероятностях состояний среды (природы) не имеется, то лицо, принимающее решения (ЛПР), находится в условиях неопределенности.
Основной метод, позволяющий найти оптимальное решение в условиях неопределенности, состоит в формулировке некоторой гипотезы о поведении среды, позволяющей дать каждому альтернативному решению числовую оценку.
Рассмотрим некоторые критерии, используемые при выборе оптимальной стратегии игрока А в условиях неопределенности.
1. Критерий Бейеса – Лапласа. В качестве оптимальной выбирается та стратегия, которая дает максимум математического ожидания выигрыша, т.е.
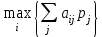,где рj– вероятность реализации состояния Пj.
Поскольку в нашем примере вероятности неизвестны, то предполагается равновероятность состояний природы (критерий Лапласа).
В столбце Мi таблицы указаны средние арифметические
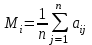.Из величин Mi максимальное значение равно 45, следовательно, оптимальной является стратегия А4.
2. Максиминный критерий Вальда (критерий пессимиста). В качестве оптимальной выбирается та стратегия, при которой минимальный выигрыш максимален, т.е.
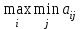
Критерий является пессимистическим, поскольку считается, что природа будет действовать наихудшим образом для человека.
В столбце αi таблицы указаны
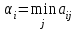. Из величин αi максимальная величина есть 25, следовательно, оптимальной является стратегия А3.3. Критерий максимума (критерий оптимиста). В качестве оптимальной выбирается та стратегия, при которой максимальный выигрыш максимален, т.е.
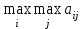
Критерий является оптимистическим, поскольку считается, что природа будет наиболее благоприятна для человека.
В столбце ωi таблицы указаны
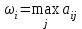
. Из величин ωi максимальная равна 85, следовательно, оптимальной является стратегия А4.
4. Критерий Гурвица. В качестве оптимальной выбирается та стратегия, при которой максимально линейная комбинация минимального и максимального выигрышей, т.е.
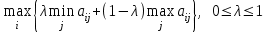,где λ – показатель пессимизма.
Если λ =1, критерий Гурвица превращается в пессимистический критерий Вальда, а при λ = 0 – в критерий крайнего оптимизма. Обычно показатель λ принимается в пределах от 0,5 до 0,7. Пусть λ = 0,6.
В столбце γi таблицы указаны γi = 0,6 αi+ 0,4 ωi. Из величин γi максимальная равна 47, следовательно, оптимальной является стратегия А3.
5. Критерий Сэвиджа (критерий сожалеющего пессимиста). В качестве оптимальной выбирается та стратегия, при которой минимален максимальный риск, т.е.
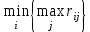
Риском называют разность между выигрышем, который можно получить, если знать действительное состояние природы, и выигрышем, который будет получен при отсутствии этой информации, т.е.
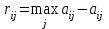.Матрица риска будет иметь в нашем случае следующий вид:
| Матрица риска | Расчетный показатель δi | |||
| | П1 | П2 | П3 | |
| А1 А2 А3 А4 | 65 10 60 0 | 50 60 0 75 | 30 10 20 0 | 65 60* 60* 75 |
В столбце δi построенной матрицы риска указаны
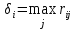. Из величин δi минимальная равна 60, следовательно, оптимальной является любая из стратегий А2, А3.Каждый из рассмотренных критериев не может быть признан вполне удовлетворительным для окончательного выбора решений, однако их совместный анализ позволяет более наглядно представить последствия принятия тех или иных управленческих решений.