ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 201
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Переменные: х1, х2 – количество единиц соответствующего вида продукта Р1, Р2.
Ограничения. Ограничение на содержание питательных веществ в рационе можно записать в следующем виде
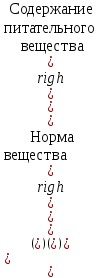.Это приводит к следующей системе ограничений:
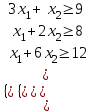
Кроме того, переменные должны быть неотрицательными.
, 
- условие неотрицательности.Целевая функция – общая стоимость рациона:
, 
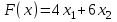.Требуется минимизировать стоимость рациона при заданных ограничениях, т.е.
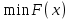.Экономико-математическая модель задачи кратко записывается в виде
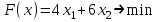
при ограничениях
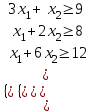
, - условие неотрицательности.Общая задача линейного программирования
Общая задача линейного программирования (ОЗЛП) ставится следующим образом. Найти экстремум (максимум или минимум) линейной целевой функции
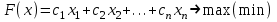
при ограничениях
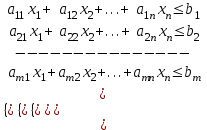
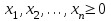- условие неотрицательности,где xj
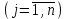– переменные; aij, bi, cj – заданные постоянные величины.В системе ограничений неравенства могут быть направлены в ту или иную сторону (, ).
Допустимым решением (планом) ОЗЛП называется вектор x = (x1, x2,…, xn), удовлетворяющий системе ограничений и условию неотрицательности.
Областью допустимых решений (ОДР) называется множество всех допустимых решений ОЗЛП.
Оптимальным решением ОЗЛП называется допустимое решение, при котором целевая функция достигает своего экстремального значения.
Геометрическая интерпретация ОЗЛП
Рассмотрим ОЗЛП с двумя переменными (на плоскости).
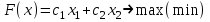
при ограничениях
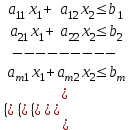
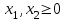- условие неотрицательности.Свойства решений ОЗЛП тесно связаны со свойствами выпуклых множеств. Рассмотрим на плоскости множество точек
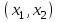.Множество точек на плоскости называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий их; в противном случае называется невыпуклым.
Примеры выпуклых и невыпуклых множеств показаны на рис.
Точка А называется внутренней точкой выпуклого множества, если в сколь угодно малой окрестности этой точки содержатся только точки этого множества.
Точка В называется граничной точкой выпуклого множества, если в сколь угодно малой окрестности этой точки содержатся как точки данного множества, так и не принадлежащие ему.
Точка С называется угловой точкой выпуклого множества, если она является граничной и не лежит внутри отрезка, соединяющего две другие точки этого множества.
Множество называется замкнутым, если оно включает все свои граничные точки.
Множество называется ограниченным, если существует окружность радиуса конечной длины с центром в любой точке множества, которое полностью содержит в себе данное множество; в противном случае называется неограниченным.
Пересечением выпуклых множеств называется множество, представляющее общую часть данных множеств.
Свойство: Пересечение выпуклых множеств есть выпуклое множество.
Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек.
Полуплоскостью называется множество точек на плоскости, координаты которых удовлетворяют неравенству
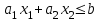.Уравнение
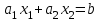является граничной прямой полуплоскости.Граничная прямая делит плоскость на две полуплоскости. Для определения, на какую сторону от граничной прямой расположена данная полуплоскость, надо взять произвольную точку на плоскости, и подставить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, иначе – в противоположную. Направление полуплоскости на рисунках штрихуется.
Полуплоскости являются выпуклыми множествами. Каждое из неравенств системы ограничений определяет полуплоскость. Система ограничений в виде неравенств (пересечение) образует выпуклое множество, которое называется многоугольником решения задачи. Стороны этого многоугольника лежат на граничных прямых, а угловые точки определяются как точки пересечения смежных граничных прямых.
Геометрически задача ЛП представляет отыскание такой точки многоугольника решений, координаты которого доставляют линейной функции F(x) экстремум, причем допустимыми решениями служат все точки многоугольника решений.
Теорема. Если задача ЛП имеет оптимальное решение, то оно достигается в одной из угловых точек многоугольника решений.
Графическое решение задач ЛП. Наиболее простым и наглядным методом ЛП является графический метод. Он применяется для решения задач ЛП с двумя переменными (на плоскости).
Рассмотрим задачу об использовании ресурсов.
при ограничениях
, - условие неотрицательности.
Решим данную задачу графическим методом.
▼ Каждое неравенство системы ограничений определяет полуплоскость с граничной прямой:
L1: 2x1 + 4x2 = 2000;
L2: 4x1 + x2 = 1400;
L3: 2x1 + x2 = 800.
Условие неотрицательности определяют полуплоскости с граничными прямыми x1 = 0, x2 = 0.
Для нахождения области допустимых решений (ОДР) строим граничные прямые. На плоскости прямую линию можно провести через две характерные точки, отсекаемые прямой на координатных осях.
Для построения граничных прямых определим их характерные точки.
L1: 2x1 + 4x2 = 2000
x1 = 0 x2 = 500, точка (0; 500);
x2 = 0 x1 = 1000, точка (1000; 0).
L2: 4x1 + x2 = 1400
x1 = 0 x2 = 1400, точка (0; 1400);
x2 = 0 x1 = 350, точка (350; 0).
L3: 2x1 + x2 = 800
x1 = 0 x2 = 800, точка (0; 800);
x2 = 0 x1 = 400, точка (400; 0).
Прежде чем строить на плоскости граничные прямые, введем еще ряд необходимых характеристик графического решения задач ЛП.
Линией уровня функции F(x) называется множество точек (x1, x2) на плоскости, в которых функция принимает одно и то же значение, т.е. F(x)= С.
Уравнение линии уровня целевой функции есть 40х1 + 60х2 = С (семейство параллельных прямых).
Вектор n = (40, 60) указывает направление наибольшего возрастания целевой функции F(x) и перпендикулярен линиям уровня F(x)= С. Построим линию уровня F(x) = С, приняв С = 9600, т.е. линия уровня линия уровня определяется выражением 40х1 + 60х2 =9600.
Замечание. Константа С = 9600 выбрана из условия, чтобы пересечения прямой линии уровня с координатными осями были целыми числами.
Линию уровня 40х1 + 60х2 = 9600 строим по двум характерным точкам:
x1 = 0 x2 = 160, точка (0; 160);
x2 = 0 x1 = 400, точка (400; 0).
На листе Excel заносим все характерные точки, определяющие граничные прямые и линию уровня. Используя графические средства Excel, строим все перечисленные прямые.
На рис. показаны граничные прямые и ОДР (заштриховано).
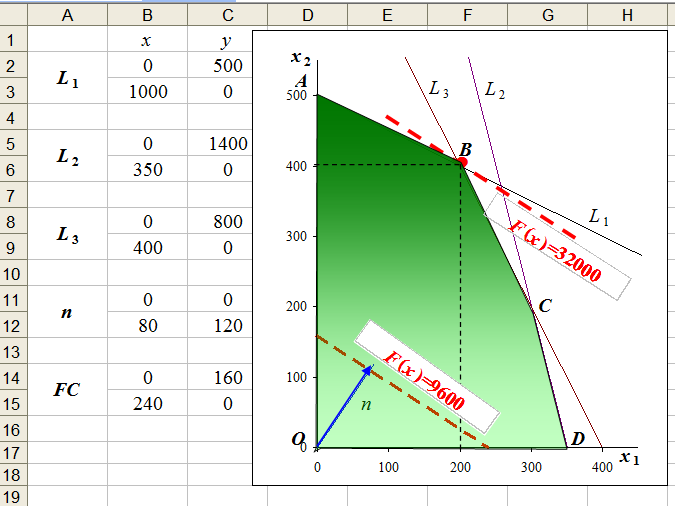
Рис. Оптимальное решение модели
Среди точек этого многоугольника нужно найти такую точку, в которой линейная функция F = 40x1 + 60x2 принимает максимальное значение.
Перемещая линию уровня параллельно самой себе до тех пор, пока у нее не окажется только одна общая точка с многоугольником решения (угловая точка В), получим оптимальное решение задачи ЛП, соответствующее максимальному значению целевой функции.
Координаты точки В(200; 400).
Таким образом, графический способ решения задачи дает оптимальное решение:
, 
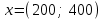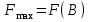= 40·200 + 60·400 = 32000.Это значит, чтобы получить максимальный доход в размере 32000 усл. ед., необходимо запланировать производство 200 единиц продукции Р1 и 400 единиц продукции Р2.
Статус ресурсов. Ограничения линейной модели классифицируются на связывающие и не связывающие.
Граничная прямая, представляющее связывающее ограничение, проходит через оптимальную точку; в противном случае ограничение является не связывающим, На рис. связывающими ограничениями являются ограничения, представленными прямыми L1, L3, а не связывающее ограничение представлено прямой L2.
Статус ресурса (дефицитным или недефицитным) устанавливается в зависимости от того, полное или частичное их использование предусматривает оптимальное решение задачи. Если ограничение является связывающим, то этот ресурс относится к дефицитному (используется полностью). Если ограничение является не связывающим, то ресурс относится к недефицитному, следовательно, ресурсы 1, 3 являются дефицитными, а ресурс 2 - недефицитным.
Решение задач ЛП в Excel
Решение задач линейного программирования можно произвести с помощью надстройки MS Excel «Поиск решения». Надстройка становится доступной при установке MS Excel. Однако, чтобы использовать эту надстройку в Excel, необходимо сначала загрузить ее.
Загрузка надстроек Поиск решения и Анализ данных