Файл: 1 Теоретические основы анализа рынка недвижимости 5.docx
Добавлен: 12.12.2023
Просмотров: 177
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Составим однофакторную линейную модель парной регрессии, описывающую зависимость цены квартиры от ее удаленности от основного района. В качестве фактора была отобрана удаленность, поскольку именно от нее в наибольшей степени зависит стоимость квартиры. Для подтверждения этого была получена матрица парных коэффициентов корреляции (см. табл. 3).
Таблица 3 – Матрица парных коэффициентов корреляции
| | Площадь общая, м2 | Площадь жилая, м2 | Этаж | Лифт | Цена квартиры, тыс. руб. |
| Площадь общая, м2 | 1 | | | | |
| Площадь жилая, м2 | 0,74694254 | 1 | | | |
| Этаж | 0,37581289 | 0,234732848 | 1 | | |
| Лифт | 0,18974111 | -0,12336321 | 0,36369648 | 1 | |
| Цена квартиры, тыс. руб. | 0,79696381 | 0,494882283 | 0,46740289 | 0,43843179 | 1 |
Как видно из таблицы 3, коэффициенты корреляции между лифтом и ценой квартиры меньше, чем все остальные коэффициенты корреляции между фактором результатов.
Положительное значение коэффициента корреляции между ценой квартиры и жилой площадью, а также между ценой квартиры и общей площадью свидетельствует о том, что с ростом площади квартиры ее цена увеличивается.
Положительное значение коэффициента корреляции между ценой квартиры и этажом говорит о том, что если квартира находится на первом и последних этажах, то при прочих равных условиях она стоит дешевле, чем, если она находится на других этажах. Положительное значение корреляции между ценой квартиры и наличием лифта в доме говорит о том, что квартиры с отсутствием лифта в домах стоят дороже. Так же стоит отметить, что значение корреляции между ценой квартиры и общей площадью самое высокое.
Результаты регрессионного анализа для линейной однофакторной модели, показывающей зависимость между общей площадью и ценой квартиры, представлены в таблице 4.
Таблица 4 – Результаты регрессионного анализа для линейной однофакторной модели, показывающей зависимость между общей площадью квартиры и ценой квартиры
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | 12,33 | 2,96 | 4,16 | 0,00 | 6,27 | 18,40 | 6,27 | 18,40 |
| Площадь общая, м2 | 0,01 | 0,00 | 6,98 | 0,00 | 0,00 | 0,01 | 0,00 | 0,01 |
Экономическая интерпретация полученных коэффициентов регрессии выглядит следующим образом: чем больше общая площадь квартиры, тем выше ее стоимость 0,01 тыс. руб. Полученное уравнение регрессии имеет следующий вид:
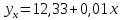
где х – цена квартиры; ух – общая площадь (тыс. руб.).
T-критерий Стьюдента используется для определения статистической значимости различий средних величин.
Табличное значение t-критерия Стьюдента при количестве наблюдений 30 равно 2,05. В нашем случае коэффициент регрессии является статистически значимым, поскольку фактическое значение t-критерия Стьюдента больше табличного (4,16 больше 2,05). Параметр регрессии является статистически значимым, поскольку фактическое значение t-критерия Стьюдента больше табличного (6,92 больше 2,05).
Совместим фактические и прогнозные значения на одном графике (см. рис.4)
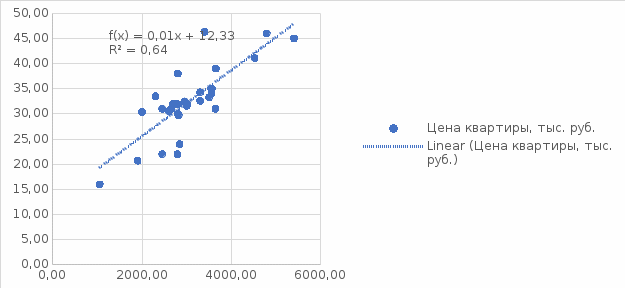
Рисунок 4 – Совмещение фактических и модельных данных
Согласно шкале Чеддока теснота связи между общей площадью и стоимостью квартиры заметная (таблица 5) поскольку множественный коэффициент корреляции равен 0,90. Возведя коэффициент корреляции в квадрат получаем коэффициент детерминации. В нашем случае он равен 0,64 это говорит о том что стоимость квартиры на 64% зависит от общей площади и на 36% от прочих факторов не включённых в модель.
Таблица 5 – Проверка качества моделей
| Показатель | Значение |
| Множественный R | 0,80 |
| R-квадрат | 0,64 |
| Нормированный R-квадрат | 0,62 |
| Стандартная ошибка | 4,31 |
| Наблюдения | 30,00 |
Табличное значение критерия Фишера – 4,20. В данном случае фактическое значение – 48,74, то есть больше критического. Это говорит о том, что уравнение регрессии является статистически значимым (см. табл. 6).
Таблица 6 – Дисперсионный анализ
| | df | SS | MS | F | Значимость F |
| Регрессия | 1,00 | 903,66 | 903,66 | 48,74 | 0,00 |
| Остаток | 28,00 | 519,09 | 18,54 | | |
| Итого | 29,00 | 1422,75 | | | |
Это свидетельствует о том, что полученная модель может использоваться для прогнозирования стоимости квартиры исходя из ее удаленности.
Перейдем к построению многофакторной линейной модели, отображающей зависимость стоимости квартиры от таких факторов как: площадь общая, площадь жилая, этаж, лифт. Поскольку несколько коэффициентов межфакторной корреляции превышают 0,7, то есть между факторами присутствует сильная линейная связь в модель включим все факторы (табл. 3 и 7).
Таблица 7 – Регрессионный анализ линейной многофакторной модели
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | 119,83 | 544,63 | 0,22 | 0,83 | -1001,86 | 1241,52 | -1001,86 | 1241,52 |
| Площадь общая, м2 | 92,45 | 21,27 | 4,35 | 0,00 | 48,64 | 136,26 | 48,64 | 136,26 |
| Площадь жилая, м2 | -19,72 | 49,54 | -0,40 | 0,69 | -121,76 | 82,32 | -121,76 | 82,32 |
| Этаж | 197,19 | 216,43 | 0,91 | 0,37 | -248,56 | 642,93 | -248,56 | 642,93 |
| Лифт | 412,68 | 204,30 | 2,02 | 0,05 | -8,09 | 833,45 | -8,09 | 833,45 |
Экономическая интерпретация полученных коэффициентов регрессии выглядит следующим образом: с увеличением общей площади квартиры на 1 м2 ее стоимость в среднем возрастет на 92,45 тыс. руб., с увеличением жилой площади квартиры на 1 м2 ее стоимость в среднем снизится на 19,72 тыс. руб., если квартира находится на первом или последних двух этажах ее стоимость вырастет на 197,19 тыс. руб., если в доме находится лифт, то ее стоимость увеличится на 412,68 тыс. руб.
Полученное уравнение регрессии имеет следующий вид:
уx =119,83 + 92,45 x1 – 19,72 х2 + 197,19 х3 + 412,68 x4,
где ух – стоимость квартиры (руб.); x1 – площадь общая (м2); x2 – площадь жилая (м2); x3 – этаж; x4 – лифт.
Табличное значение t-критерия Стьюдента при количестве наблюдений 30 равно 2,05. Первый параметр регрессии является статистически значимым, поскольку фактическое значение t-критерия Стьюдента больше табличного (4,35 больше 2,05), второй параметр регрессии является статистически незначимым, поскольку фактическое значение t-критерия Стьюдента больше табличного (-0,4 меньше 2,05), третий параметр регрессии является статистически незначимым, поскольку фактическое значение t-критерия Стьюдента больше табличного (0,91 меньше 2,05), четвертый параметр регрессии является статистически незначимым, поскольку фактическое значение t-критерия Стьюдента меньше табличного (2,02 меньше 2,05).
Качество подбора модели определяется так же с помощью показателей таблицы 8.
Таблица 8 – Регрессионная статистика многофакторной линейной модели
| Регрессионная статистика | |
| Множественный R | 0,85493 |
| R-квадрат | 0,7309 |
| Нормированный R-квадрат | 0,68785 |
| Стандартная ошибка | 475,717 |
| Наблюдения | 30 |
Как видно из сравнений таблицы 5 и 8 переход к многофакторной линейной модели позволил улучшить ее качество.
Заключение
В данной курсовой работе был разобран рынок первичного жилья однокомнатных квартир Кировского района г.о. Самары. Для получения информации был использован сайт: https://samara.cian.ru/.
В первом разделе работы были рассмотрены теоретические основы анализа рынка недвижимости, а именно: понятие, сущность и виды недвижимости, сущность, виды и функции рынка недвижимости, и сущность корреляционно-регрессионного анализа.
Во втором разделе работы была дана краткая характеристика Кировского района города Самары, была произведена экономико-математическая модель, которая позволила определить стоимость однокомнатных квартир на первичном рынке в Кировском районе г.о. Самара, для чего было отобрано 30 типовых квартир.