Файл: Тема Случайные события и действия над ними. Классическое и статистическое определение вероятностей.docx

(33)

С1

Модуль 8.Теория вероятностей и математическая статистика

С2

Тема 1. Случайные события и действия над ними. Классическое и статистическое определение вероятностей

С3

Предмет теории вероятностей

Все события делятся на 3 группы (вида):

Достоверное – событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.

Пример: при нормальном атмосферном давлении и t=20^оC событие «вода в стакане в жидком состоянии» достоверно.

Невозможное – событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий S.

Пример: событие «вода в стакане в твердом состоянии» при тех же условиях заведомо не произойдет.

Случайное – событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти.

Пример: если брошена монета, то событие «выпал орел» случайное.

Совокупность условий влияющих на выпадение орла: сила, с которой брошена монета, форма монеты и др.
С4

Невозможно учесть действия всех этих причин на результат.

Теория вероятностей не ставит перед собой задачу предсказать событие.

Другое дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т.е. речь идет о массовых однородных случайных событиях.

Достаточно большое число однородных случайных событий независимо от природы подчиняются определенным закономерностям, а именно вероятным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.

Предметом теории вероятностей является изучение вероятных закономерностей массовых однородных случайных событий.
С5

Случайные события

«Совокупность условий S осуществлена» <=> «произведено испытание» т.е. событие будет рассматриваться как результат испытания.

Пример 1. Стрелок стреляет по мишени разделенной на четыре области. Выстрел – это испытание. Попадание в определенную область – событие.

Пример 2. В урне имеются цветные шары. Из урны наудачу берут один шар. Испытание – извлечение шара. Событие – появление шара определенного цвета.

События называются

---

несовместимыми, если появление одного из них исключает появление других событий в одном и том же испытании.

Пример: Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместимые.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

Если события, образующие полную группу, попарно несовместимы, то в результате испытания появится одно из этих событий.

Пример: Стрелок произвел выстрел по цели. Обязательно произойдет одно из двух следующих событий: попадание, промах. Эти два несовместимых события образуют полную группу.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Пример: Появление «герба» или «надписи» при бросании монеты – равновозможные события.

Пример: Появление того или иного числа очков на брошенной игральной кости – равновозможные события.
С6

Классическое определение вероятности

Существует несколько определений вероятности. Рассмотрим пример:

Пусть в урне 6 одинаковых шаров: (тщательно перемешанных) 2 – красных, 3 – синих, 1 – белый. Очевидно, возможность вынуть из урны цветной (красный или синий) больше, чем белый. Можно ли охарактеризовать эту возможность числом?

Да. Это число называют вероятностью события. Т.е., вероятность – есть число, характеризующее степень возможности того, что взятый наудачу шар цветной. Обозначим, А – событие «появление цветного шара» Испытание – извлечение шара из урны. Каждый из возможных результатов испытания, назовем элементарным исходом (элементарным событием)
С7

Элементарный исход:

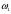- появляется белый шар;

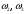- появляется красный шар;

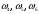- появляется синий шар.

Все эти исходы образуют полную группу попарно несовместимых событий.

Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующим этому событию.

В нашем примере благоприятствующими событию А следующие 5 исходов:



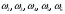
Т.е., событие А наблюдается, если наступает один из исходов, благоприятствующих А: в нашем примере

---

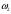
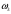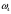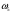, или , или , или , или .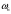

В этом смысле событие А подразделяется на несколько элементарных событий ( ), элементарное событие не подразделяется на другие события.

Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают Р(А).

В примере: всего элементарных исходов 6, из них 5 благоприятствующие событию А Р(А)= .
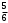С8

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Р(А)= ,

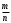где m – число элементарных исходов, благоприятствующих А;

n – число всех возможных элементарных исходов испытания.

Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.
С9

Свойства из определения вероятности:

Свойство 1. Вероятность достоверного события равна единице:

Р(А)=

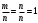
Действительно, если событие достоверное, то каждый элементарный исход испытания благоприятствует событию

m = n

Свойство 2. Вероятность невозможного события равна нулю.

Р(А)= .

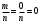Действительно, если событие невозможно, то один из элементарных исходов испытания не благоприятствует событию.

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания

, т.е. 0 < P(A) < 1

вероятность любого события:
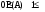
С10

Статическая вероятность

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно.

Часто невозможно представить результат испытаний в виде совокупности элементарных событий.

---

Трудно указать основания, позволяющие считать элементарные события равновозможными.

Поэтому используют другие определения:

Статическое определение вероятности: в качестве статической вероятности, события принимают относительную частоту или число, близкое к ней.

Для существования статической вероятности события А требуется:

Возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А или наступает или не наступает;

устойчивость относительных частот появления А в различных сериях достаточно большого числа испытаний.

С11

Тема 2 Аксиомы теории вероятностей, следствия из аксиом. Геометрическая вероятность.

С12

Пусть в результате испытания наступает одно и только одно из событий



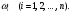
События 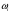называют элементарными событиями (элементарными исходами).

Уже отсюда следует, что элементарные события попарно несовместимы.

Множество всех элементарных событий, которые могут появиться в испытаниях, называют пространством элементарных событий 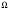, а сами элементарные события – точками пространства .

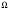Событие А отождествляют с подмножеством (пространства 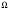), элементы которого есть элементарные исходы, благоприятствующие .
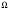С13

Множество всех событий, которые могут наступить в испытании, есть множество всех подмножеств .

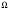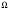- достоверное событие; пустое подмножество пространства 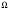- невозможное событие.

Каждому элементарному исходу 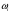ставят в соответствие число р_i – вероятность этого исхода, причем .

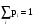По определению, вероятность Р(А) события равна сумме вероятностей элементарных исходов, благоприятствующих А.

Поэтому вероятность достоверного события равна единице, невозможного – нулю, произвольного – заключена между нулем и единицей.

---

Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятности.

В системе аксиом, предложенной А, Н. Колмогоровым, неопределяемыми понятиями являются элементарное событие и вероятность.
С14

Аксиомы определяющие вероятность:

Каждому событию А поставлено в соответствие неотрицательное действительное число Р(А). Это число называется вероятностью события А.

Вероятность достоверного события равна единице.

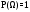
Вероятность наступления хотя бы одного из попрано несовместимых событий равна сумме вероятностей этих событий.
С15

Геометрические вероятности

Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов, поэтому вводится геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).

Пусть отрезок l составляет часть отрезка L.

На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка к длине отрезка L.

С16

В этих предположениях вероятность попадания точки на отрезок l определяется равенством


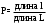
С17

Пример 1. На отрезке ОА длинны L числовой оси ОХ наудачу поставлена точка В(Х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеют длину, большую .

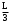Решение:

ОС=CD=DA=

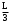
Требование задачи будет выполнено, если
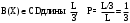
С18

Пример 2. Пусть плоская фигура g составляет часть плоской фигуры G. На G брошена наудачу точка. Вероятность попадания точки в область g равна

С19

Пример. Две концентрические окружности R=10, r=5. Найти вероятность того, что брошенная наудачу в большой круг точка, попадет в кольцо.

---