Файл: Тема Случайные события и действия над ними. Классическое и статистическое определение вероятностей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение. Площадь кольца
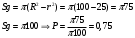
Замечание 1. Приведенные определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу в область g – часть области G,
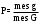
Замечание 2. В случае классического определения вероятность достоверного события равна 1, невозможно равенство 0, верны обратные утверждения, т.е. если вероятность равна 1, то событие достоверное, если вероятность события равна 0, то событие невозможно.
В геометрическом определении вероятности обратные утверждения не имеют места.
С20
Тем 3. Теорема сложения вероятностей. Теорема сложения вероятностей несовместимых событий
С21
Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.
Пример. Из орудия произвели два выстрела. Событие А – попадание при первом выстреле, В – попадание при втором выстреле. А+В – попадание при первом выстреле или попадание при втором выстреле, или в обоих выстрелах.
Если А и В несовместимые события, то А+В – событие состоящее в появлении одного из этих событий.
Суммой нескольких событий называют событии, которое состоит в появлении хотя бы одного из этих событий.
С22
Теорема сложения несовместимых событий.
Вероятность появления одного из двух несовместимых событий, безразлично какого, равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B).
Доказательство: пусть n – общее число возможных элементарных исходов испытания, m1 – число исходов, благоприятствующих событию А, m2 – число исходов, благоприятствующих событию В.
Число элементарных исходов благоприятствующих событию А, либо событию В, равно m1+m2, значит
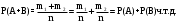
С23
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
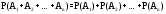
Доказательство проводиться методом индукции.
Пример 1. В урне 30 шаров: 10 – красных, 5 – синих, 15 – белых. Найти вероятность появления цветного шара.
Вероятность появления красного:
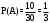
Вероятность появления синего:
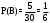
События А и В несовместны, поэтому можно применить теорему сложения
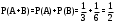
С24
Полная группа событий
Теорема. Сумма вероятностей событий
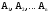, образующих полную группу равна единице: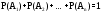 
Доказательство: т.к. события
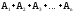- это достоверные события, то 
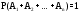. Любые два события полной группы несовместны, значит можно применить теорему сложения 
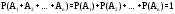. ч.т.д.С25
Противоположные события
Противоположными называют два единственно возможных события, образующих полную группу. Обозначение:
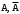
Пример. 1) Попадание и промах при выстреле по цели – противоположные события
2) При бросании монеты: выпадение герба или надписи – противоположные события.
Теорема. Сумма вероятностей противоположных событий равна единице:
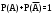
Доказательство: Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице.
Замечание. При решении задач на нахождение вероятности события А часто выгодно сначала вычислить вероятность события
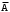, а затем найти вероятность по формуле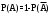 
С26
Теорема сложения вероятностей совместных событий.
Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же событии.
Пример 1: А – появление четырех очков при бросании игральной кости, В – появление четного числа очков. События А и В совместные.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
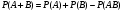
Доказательство: Т.к. А и В по условию совместны, то событие А+В наступит, если наступит одно из следующих трех несовместных событий
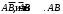
С27
По теореме сложения несовместных событий: (**)
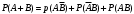Событие А произойдет, если наступит одно из двух несовместных событий: 
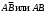По теореме сложения несовместных событий: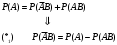 
Аналогично,
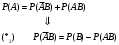
Подставим
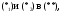получим 
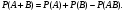ч.т.д.С28
Замечание 1: При использовании полученной формулы следует иметь в виду, что события А и В могут быть как зависимыми, так и независимыми:
для независимых событий:
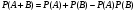
для зависимых событий:
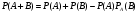
С29
Замечание 2: Если А и В несовместные события, то их совмещение есть невозможное событие, т.е.
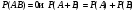
Пример: Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны
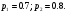Найти вероятность попадания в цель при одном залпе (из обоих орудий) хотя бы одним из орудий.Решение:
1 сл. Событие А – попадание из 1-го орудия, В – попадание из 2-го орудия, независимы.
Вероятность события AB (оба орудия дали попадание)
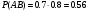
Искомая
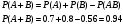
2 сл. Т.к. А, В независимы, то
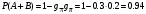
С30
Тема 4. Условная вероятность. Теорема умножения вероятностей для зависимых и независимых событий
С31
Принцип практической невозможности маловероятных событий.
При решении многих практических задач приходится иметь дело с событиями, вероятность которых близка к нулю. Можно ли считать, что маловероятное событие А в единичном испытании не произойдет? Такого заключения сделать нельзя т.к. не исключено, хотя и мало вероятно, что событие А наступит. Однако длительный опыт показывает, что маловероятное событие в единичном испытании в подавляющем большинстве случаев не наступает.
С32
Принцип практической невозможности маловероятных событий.
Если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит. Возникает вопрос? Насколько малой должна быть вероятность, чтобы можно было считать невозможным появление этого события в одном испытании? Ответить однозначно на этот вопрос нельзя. В разных задачах считают по-разному.
Пример. 1) Если вероятность того, что парашют при прыжке не раскроется, равна 0.01, то было бы недопустимым применять такие парашюты.
2) Если же считать, что вероятность того, что поезд дальнего следования прибудет с опозданием, равным 0.01, то можно практически быть уверенным, что поезд прибудет вовремя.
Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заключенные между 0.01 и 0.05. Аналогично для событий:
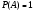.Следствие. Если случайное событие имеет вероятность, очень близкую к единице, то практически можно считать, что в единичном испытании, что событие наступит.
С33
Теорема умножения вероятностей.
Произведением двух событий А и В называют событие АВ, состоящие в совместном появлении (совмещении) этих событий.
Пример. А – деталь годная;
В – деталь окрашена,
то АВ деталь годная и окрашенная.
Произведением нескольких событий называют события, состоящее в совместном появлении этих событий.
Пример. А, В, С – выпадение герба в 1-ом, 2-ом, и 3-ем случаях, то АВС – появление герба во всех 3-х случаях.
С34
Условная вероятность.
Если при вычислении вероятности события никаких других ограничений, кроме условий S не налагается, то такую вероятность называют безусловной, если же налагаются и другие дополнительные условия, то вероятность события называют условной.
Часто вычисляют вероятность события В при дополнительном условии, что производило событие А.
Условной вероятностью
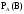называют вероятностью события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна
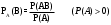
Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимали по одному шару, не возвращая обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).
Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая вероятность условная:
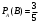
Этот же результат можно получить по формуле
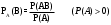(Проверить самостоятельно).С35
Теорема умножения
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
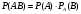(*)Доказательство. По определению условной вероятности
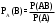
Отсюда,
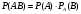.Замечание. Применив формулу (*) к событию ВА, получим
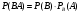
Но т.к. АВ не отличается от события ВА, то
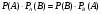
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
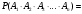
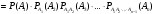, где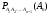 
- вероятность события 
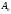, вычисленная в предположении, что события 
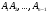наступили. В частности, для трех событий: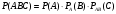 
С36
Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый валик – конусный, а второй – эллиптический.
Решение. Вероятность того, что первый валик окажется конусным (событие А);
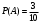. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик – конусный, т.е. условная вероятность 
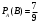. По теореме умножения, искомая вероятность 
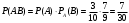, заметим, что сохранив обозначения легко найдем: 
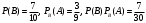.С37
Пример 2. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что извлекают один шар наудачу, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором – черный (событие В) и при третьем – синий (событие С).
Решение. Вероятность появления белого шара в первом испытании
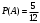.Вероятность появления черного шара во втором испытании в предположении, что в первом испытании появился белый, т.е. условная вероятность
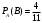.Вероятность появления синего шара в третьем испытании вычислен, в предположении, что в первом испытании появился белый шар, а во втором – черный, т.е. условная вероятность:
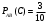.Искомая вероятность
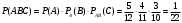.С38
Независимые события. теорема умножения для независимых событий.
Пусть вероятность события В не зависит от появления события А.
Событие В называют независимым от события А, если появление события А не изменяет вероятности появления В, т.е. если условная вероятность события В равна его безусловной вероятности:
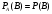, тогда 
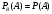.Если событие А не зависит от события В, то и событие А не зависит от события В, это означает, что свойство независимости событий взаимно.
И тогда теорема умножения для независимых событий
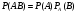имеет вид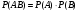 
Т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий, в противном случае события называют зависимыми.
С39
Пример. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) 0.8, а вторым (событие В) – 0.7.
Решение. События А и В независимые, по теореме умножения:
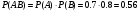
С40
Замечание 1. Если события А и В независимы, то независимы также события
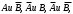действительно, 
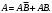Следовательно,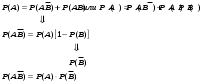 
Независимость событий
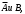
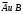следует и независимость 
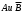.С41
Несколько событий называют попарно независимыми, если каждые два из них независимы. Т.е. А, В, С – независимы, если независимы А и В, В и С, А и С.
Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимо каждое событие и все возможные произведения остальных.
Если несколько событий независимы попарно, то отсюда не следует их независимость в совокупности. Т.е. требование независимости в совокупности сильнее требования независимости попарно.
С42
Пример. Пусть в урне 4 шара: 1 – красный (А), 1 – синий (В), 1 – черный (С), 1 – во все три цвета (АВС). Чему равна вероятность того, что извлеченный шар имеет красный цвет.
Решение. Т.к. из четырех шаров два имеют красный цвет, то
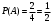. Аналогично,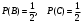 
Допустим теперь, что событие В произошло, т.е. взятый шар имеет синий цвет. Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события А по-прежнему
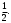
Другими словами, условная вероятность события А, вычисленная в предположении, что наступило событие В, равна его безусловной вероятности. Следовательно, события А и В независимы. Аналогично придем к выводу, что события А и С, В и С независимы.
С43
Итак, события А, В, С попарно независимы. Независимы ли эти события в совокупности? Оказывается нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероятность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Т.е.
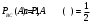.Итак, попарно независимые события А, В и С не являются независимыми в совокупности.
С44
Следствие. (из теоремы умножения)
Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
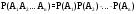
Доказательство. Рассмотрим три события А, В и С равносильно совмещению событий АВ и С, поэтому
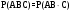. Т.к. события А, В и С независимы в совокупности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух независимых событий имеем: 
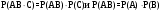Итак, окончательно получим 
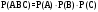, для произвольного n доказательство проводиться методом математических индукций.С44
Замечание. Если события
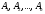независимы в совокупности, то и противоположны им события 
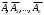также независимы в совокупности.С45
Пример 2. Найти вероятность совместного появления герба при одном бросании двух монет.
Решение. Вероятность появления герба первой монеты (событие А)
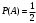. Вероятность появления герба второй монеты (событие В)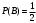 
События А и В независимые, поэтому искомая вероятность по теореме умножения равна
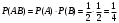.С46
Пример 3. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что их первого ящика вынута стандартная деталь (событие А),
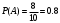
Вероятность того, что из второго ящика вынута стандартная деталь (событие В)
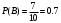
Вероятность тог, что из 3-го ящика вынута стандартная деталь (событие С)
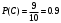
Т.к. события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения)
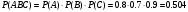
С47
Пример 4. Вероятности появления каждого из трех независимых событий
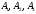соответственно равны 
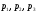. Найти вероятность появления только одного из этих событий.Решение. Появление только первого события А, равносильно появлению события
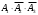(появится первое, но не появится второе и третье)Обозначим
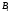- появится только 
, 
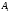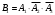
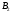- появится только , 
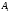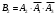
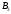- появится только 
, 
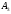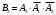
Т.е. искомая вероятность
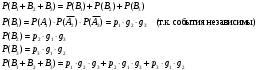
С48
Тема 5. Формула полной вероятности. Вероятность гипотез. Формулы Бейеса
С49
Формула полной вероятности
Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий
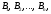образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: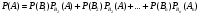 
Доказательство: По условию, событие А может наступить, если наступит одно из несовместных событий
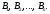Другими словами, появление события одного (безразлично какого), из событий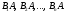 
С50
По теореме сложение:
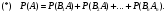
по теореме умножения зависимых событий, имеем:
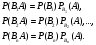
Подставив полученные соотношения в равенство (*) имеем:
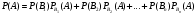ч.т.д.С51
Пример 1: Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная, равна 0.8, а второго – 0.9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная.
Решение:
А – извлеченная деталь стандартная;
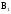– деталь извлечена из 1-го набора;
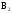– деталь извлечена из 2-го набора.
С52
Условная вероятность того, что из первого набора будет извлечена стандартная деталь
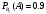
По формуле полной вероятности
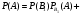
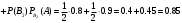
Пример 2: В первой коробке 20 радиоламп, из них 18 – стандартных, во второй: 10 – из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую коробку. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартная.
С53
Решение:
А – из первой коробки извлечена стандартная лампа;
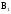– из второй коробки извлечена стандартная лампа; 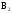– из второй коробки извлечена нестандартная. 
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй будет переложена стандартная лампа
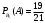
С54
Условная вероятность того, что из первой коробки будет извлечена стандартная, при условии, что из второй будет переложена нестандартная
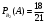
По формуле полной вероятности, искомая вероятность того, что из 1-ой коробки будет извлечена стандартная
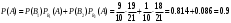
С55
Вероятность гипотез. Формулы Бейеса.
Пусть событие А может наступить при условии появления одного из несовместных событий
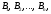образующих полную группу. Т.к. заранее неизвестно, какое из этих событий наступит, их называют гипотезами.Вероятность события А определяется по формуле полной вероятности:
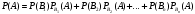
С 56
Допустим, произведено испытание, в результате которого появилось событие А. Определим, как изменились (в связи с тем, что событие А наступило) вероятности гипотез. Т.е. найдем вероятности событий:
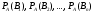
Найдем
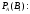по теореме умножения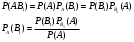
С57
Подставим P(A) из формулы (*), получим:
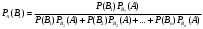
Аналогично выводятся формулы, определяются условные вероятности остальных гипотез. Т.е. условная вероятность любой гипотезы:
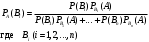
Формулы Бейеса (по имени английского математика, который их вывел в 1764 г.)
Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становиться известным результат испытания, в итоге которого появилось событие А.
С58
Пример: Детали попадают для проверки к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру – 0.6, ко второму – 0.4. Вероятность того, что деталь будет признана стандартной первым контролером – 0.94, вторым – 0.98. Годная деталь при проверке признана стандартной. Найти вероятность того, что эту деталь проверит первый контролер.
Решение: А – деталь признана стандартной;
Гипотеза
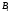– деталь проверил первый контролер; 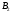– деталь проверил второй контролер.С59
Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса:
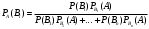
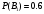(вероятность, что деталь попадает к первому контролеру)
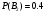(вероятность, что деталь попадает ко второму контролеру)
С60
Искомая вероятность:
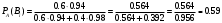
До испытания вероятность гипотезы
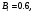а после испытания вероятность гипотезы 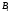стала равна 0.59.