Цель групповой работы: Сформулировать основные теоретические факты по теме, сформировать алгоритм решения задач на отыскание наибольшего и наименьшего значений непрерывной функции на промежутке.Задание группам1. Рассмотрите рисунки и ответьте на вопросы

1. 
   Непрерывна ли функция на отрезке [a;b]?
   
2. 
   Найдите стационарные и критические точки.
   
3. 
   В какой точке достигается у_наиб?
   
4. 
   В какой точке достигается у_наим?
   

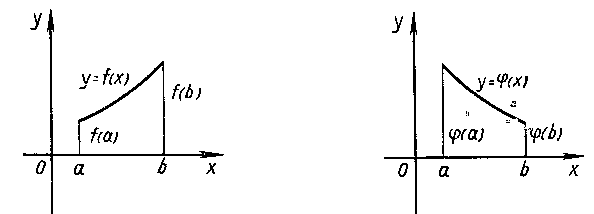1)	1) 2) 3) унаиб = f( ) 4) унаим= f( )	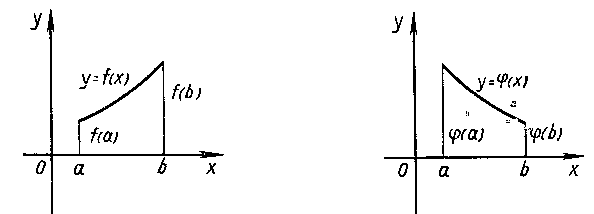2)	1) 2) 3) унаиб = ( ) 4) унаим= ( )
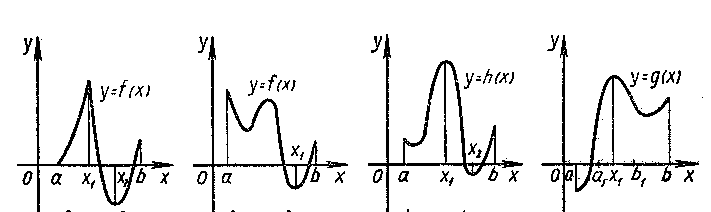3)	1) 2) 3) унаиб = f( ) 4) унаим= f( )	4)	1) 2) 3) унаиб = f( ) 4) унаим= f( )
5)	1) 2) 3) унаиб = h( ) 4) унаим= h( )	6)	1) 2) 3) унаиб = g( ) 4) унаим= g( )

---

2. Сделайте выводы:А) В каких точках функция может принимать свое наибольшее и наименьшее значения?_______________________________________________________________________Б) Если наибольшее ( наименьшее) значения функции достигаются во внутренних точках отрезка [a;b], то какие это могут быть точки?_______________________________________________________________________В) Всегда ли непрерывная на отрезке [a;b] функция имеет и наименьшее и наибольшее значение?__________________________________________3 ТЕОРИЯ . Закончите предложения.1) Если функция непрерывна на отрезке, то она достигает на нем и своего _______________и своего___________________ значения.2) Наименьшего и наибольшего значений непрерывная функция может достигать, как на ________________________, так и внутри него.3) Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в ________________________ или _____________________ точке.4. Ответьте на вопросы.1) На каких рисунках функция не имеет стационарных и критических точек?___________________________________________________________2) Охарактеризуйте монотонность функций на этих рисунках. ____________________________________________________________________________________________3) В какой точке достигаются у_наиб и у_наим, если функция убывает на отрезке [a;b]?_________________________________________________________________________4) В какой точке достигаются у_наиб и у_наим, если функция возрастает на отрезке [a;b]?_________________________________________________________________________5.Закончите предложения.ТЕОРИЯ Если функция y=f(x) не имеет на отрезке[a;b] критических и стационарных точек, тогдаа) если f´(x)>0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( _______ конце промежутка), а наименьшее в точке а (__________ конце промежутка).б) если f´(x) <0 на (а; b) f(x) – убывает на [a;b], поэтому наибольшее значение на отрезке функция принимает в _________ (___________________), а наименьшее в _____________ ( _________________________).Что необходимо знать, чтобы найти у_наиб

---

и у_наим, для функции на отрезке [a;b], если функция непрерывна на этом отрезке?1)______________________________________________________________________2)________________________________________________________________________________________________________________________6. Предложите алгоритм отыскания наибольшего и наименьшего значений функции на отрезке. ( Оформите ваш алгоритм на большом листе маркером)7. Обсудите результаты работы групп с учителем и классом. Уточните и запишите алгоритм.АЛГОРИТМ__________________________________________________________________­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________8 ТЕОРИЯ . Работайте по распечатке №2 Задания на урок. Теорема Теорема: Если функция у=f(x)непрерывна на промежутке Х и имеет внутри него единственную стационарную или критическую точку х=х₀, тогда:а)________________________________________________________б)_________________________________________________________ 0>

---

Смотрите также файлы

• Кні 07. 02. 2022 ж Малімні атыжні Самекенова Айзада Бакытжановна.docx

• Приготовление заварного теста и изделий из него.docx

• Нрслтан аласы кімідігіні.docx

• Инструкция к тесту в задании содержаться вопросы по 8 предметам химия.docx

• Рабочая программа учебного предмета.docx