АннотацияВ данной предметно-аналитической справке представлено решение студентом учебной задачи о загрузке оборудования и последующее комментирование полученных в процессе решения отчетов и результатов.

1. 
   Постановка задачи
   

Для уборки урожая с трёх полей разного рельефа фермер может использовать любые из трех комбайнов. По его оценкам производительности комбайнов и затраты на их работу на разных полях – разные (см. таблицу). Как составить оптимальный план работы комбайнов при ограниченных ресурсах времени?

Комбайны	Производительность (га/час)			Затраты (€ в час)	Ресурсы времени (час)
	поле А	поле Б	поле В
«Дон»	5	5	6	16	36
«Кубань»	5	6	4	18	24
«Неман»	7	8	6	20	15
Площадь поля (га)	150	120	180

2. 
   Математическая модель задачи
   

Управляющие переменные: 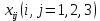часов – работает i-й комбайн на j-м поле. 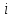=1 – «Дон»; 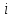=2 – «Кубань»; 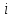=3 – «Неман».

---

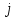=1 – «Поле А»; 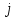=2 – «Поле Б»; 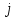=3 – «Поле В».Целевая функция – суммарные затраты (€ в час): 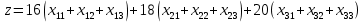→min
- слева: кол-во убранных га поля А, справа: его площадь

- аналогично, но про поле Б

- аналогично, но про поле В
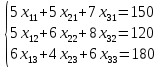
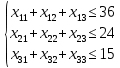
Ограничения по количеству убранных гектаров: Везде используем равенства, так как нужно полностью убрать все поля, а «лишних» гектаров нет.Ограничения на время работы каждого из комбайнов:Используем нестрогие неравенства, так как имеем возможность израсходовать либо все ресурсы, либо меньшее количество.Таким образом, имеем следующую математическую модель: 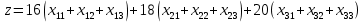→min

3. 
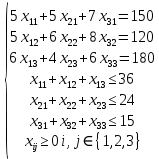
   Решение задачи
   

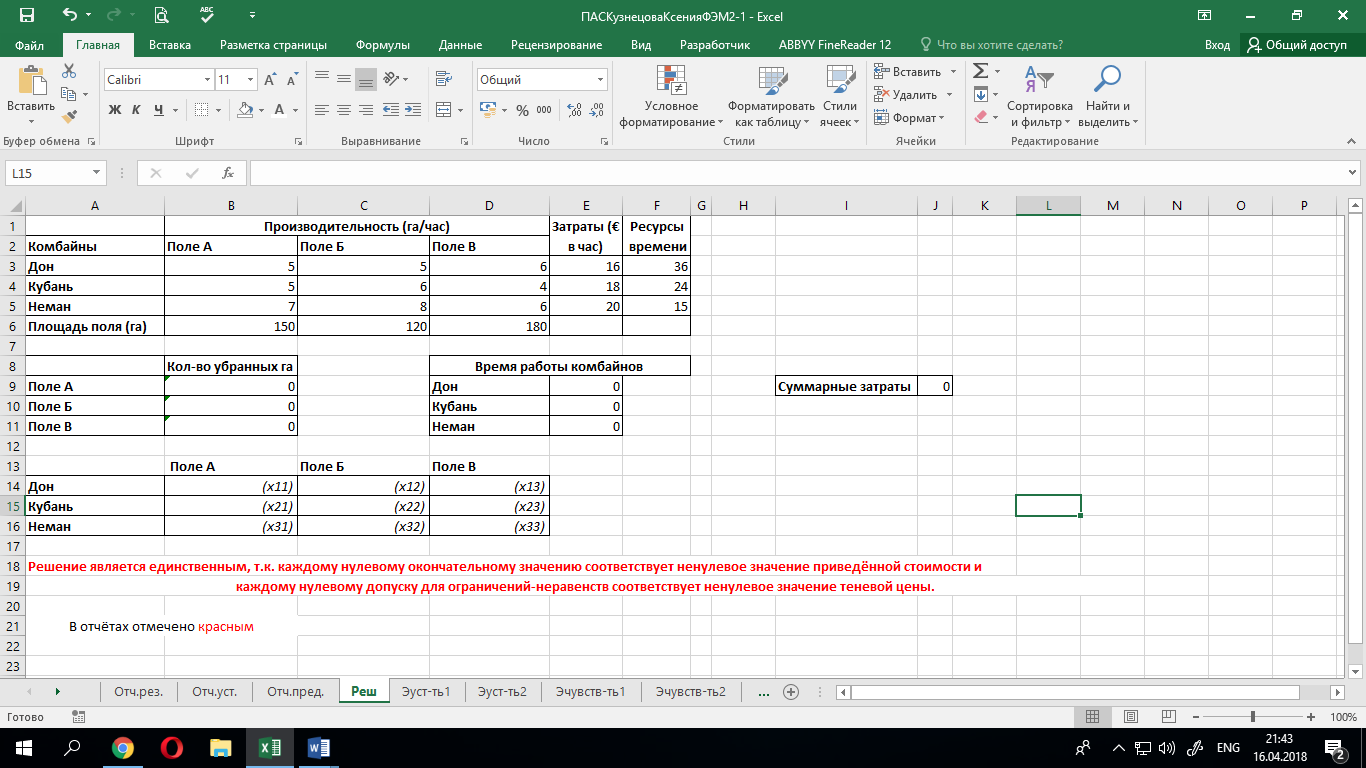
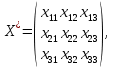
1.3.1 Рабочий листДля поиска оптимального плана обеспечивающего минимальное значение суммарных затрат 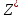при выполнении ограничений на время работы комбайнов и ограничений по количеству убранных га, используем программу «Поиск решения» в Excel.В качестве исходных данных задаем единичные значения управляющих переменных .Для вычисления левых частей трех равенств в системе ограничений используем функцию «СУММПРОИЗВ» (на рабочем листе – количество убранных га); для вычисления левых частей трех неравенств в системе ограничений используем функцию «СУММ» (на рабочем листе – время работы комбайнов).

---

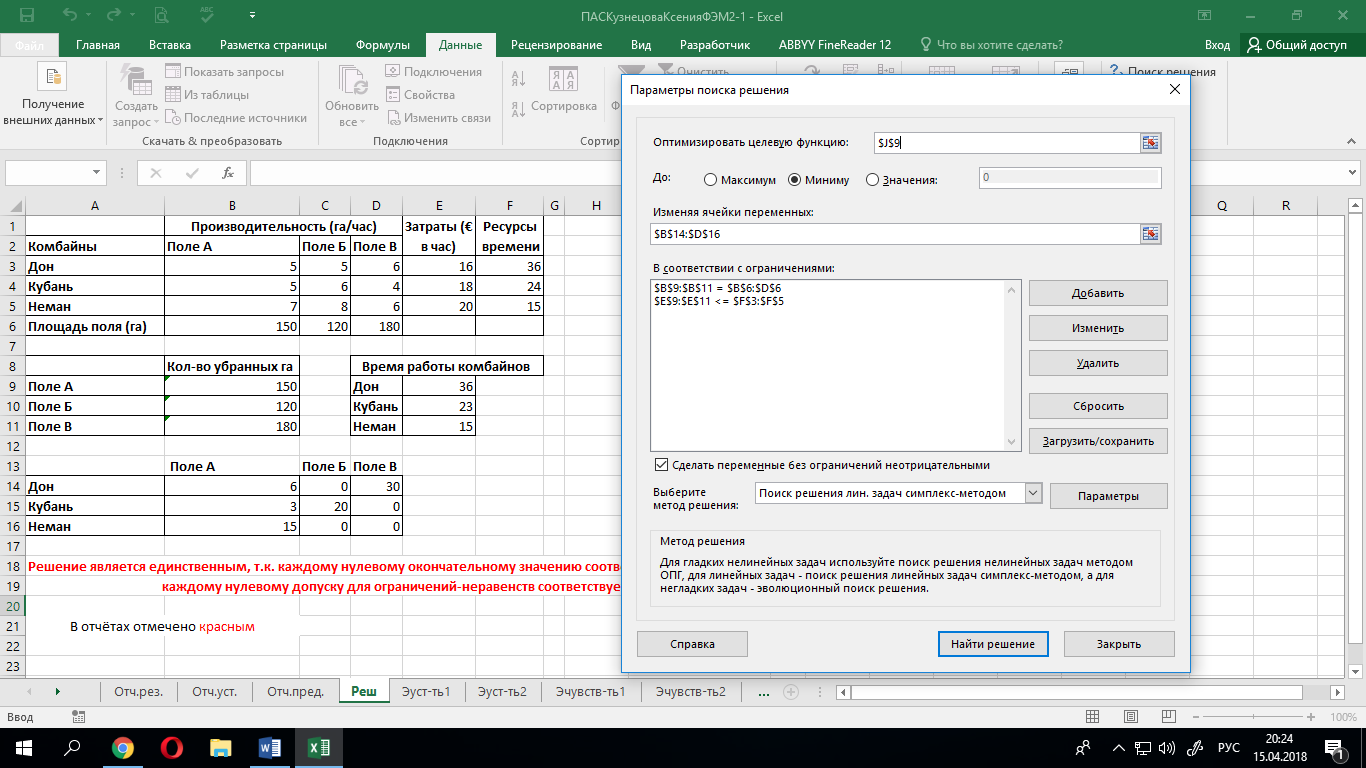
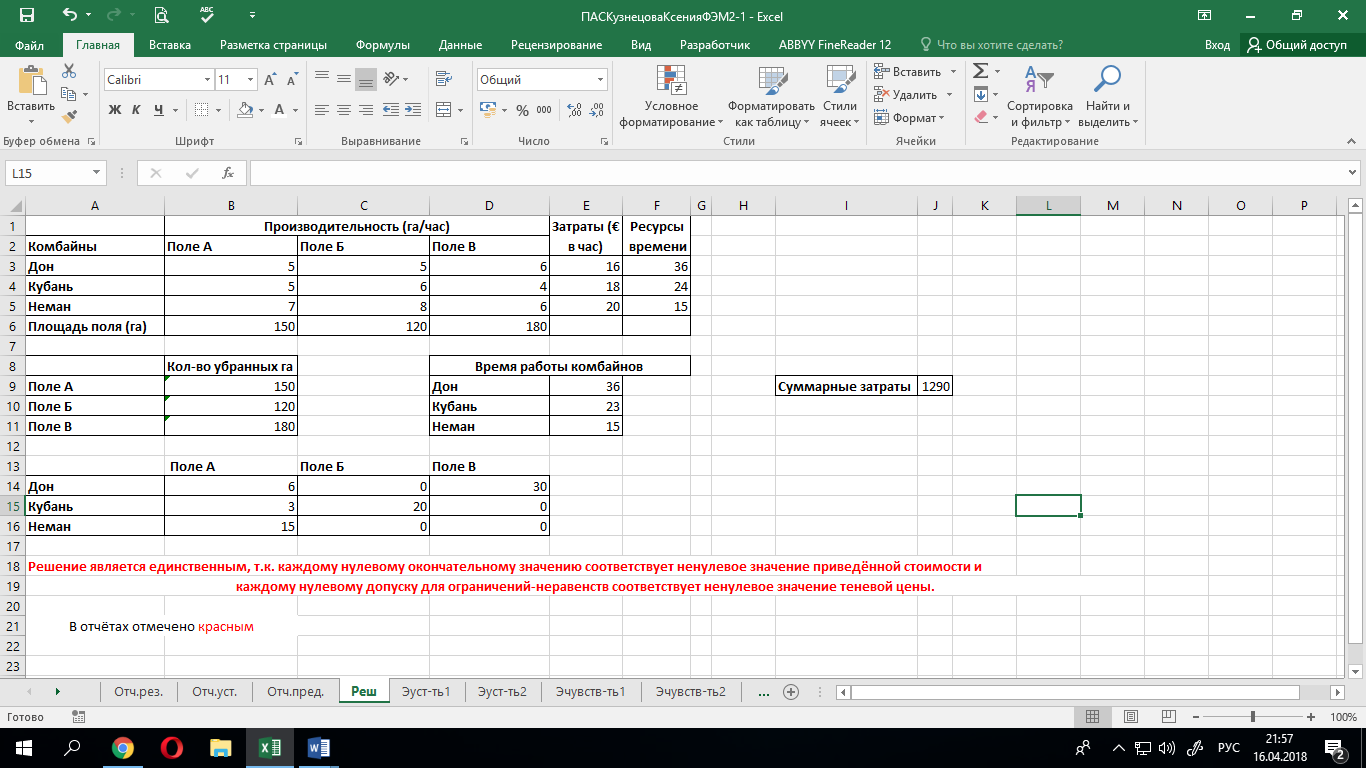
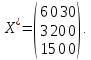
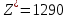
1.3.2 Параметры поиска решенияЗапустив надстройку «Поиск решения» получим следующий результат:1.3.3 Решение задачиОптимальный план работы каждого комбайна на конкретном поле (час):Минимальные суммарные затраты составят Комбайны «Дон» и «Неман» полностью израсходуют при этом имеющиеся у них в запасе ресурсы времени, а комбайн «Кубань» затратит 23 часа из 24 возможных.

4. 
   Расшифровка отчетов
   

1.4.1 Единственность решенияПредставляется целесообразным начать комментирование отчетов с ответа на вопрос «Является ли данное оптимальное решение единственным?». 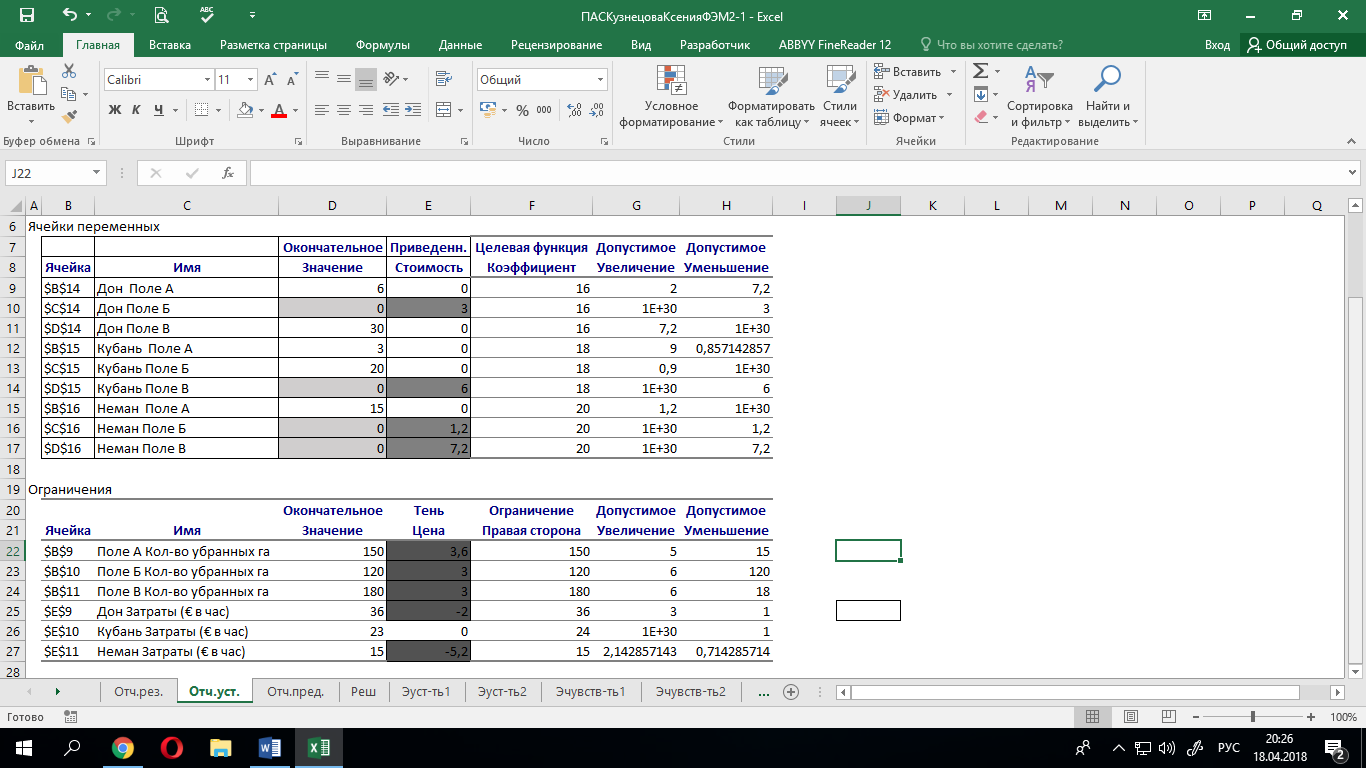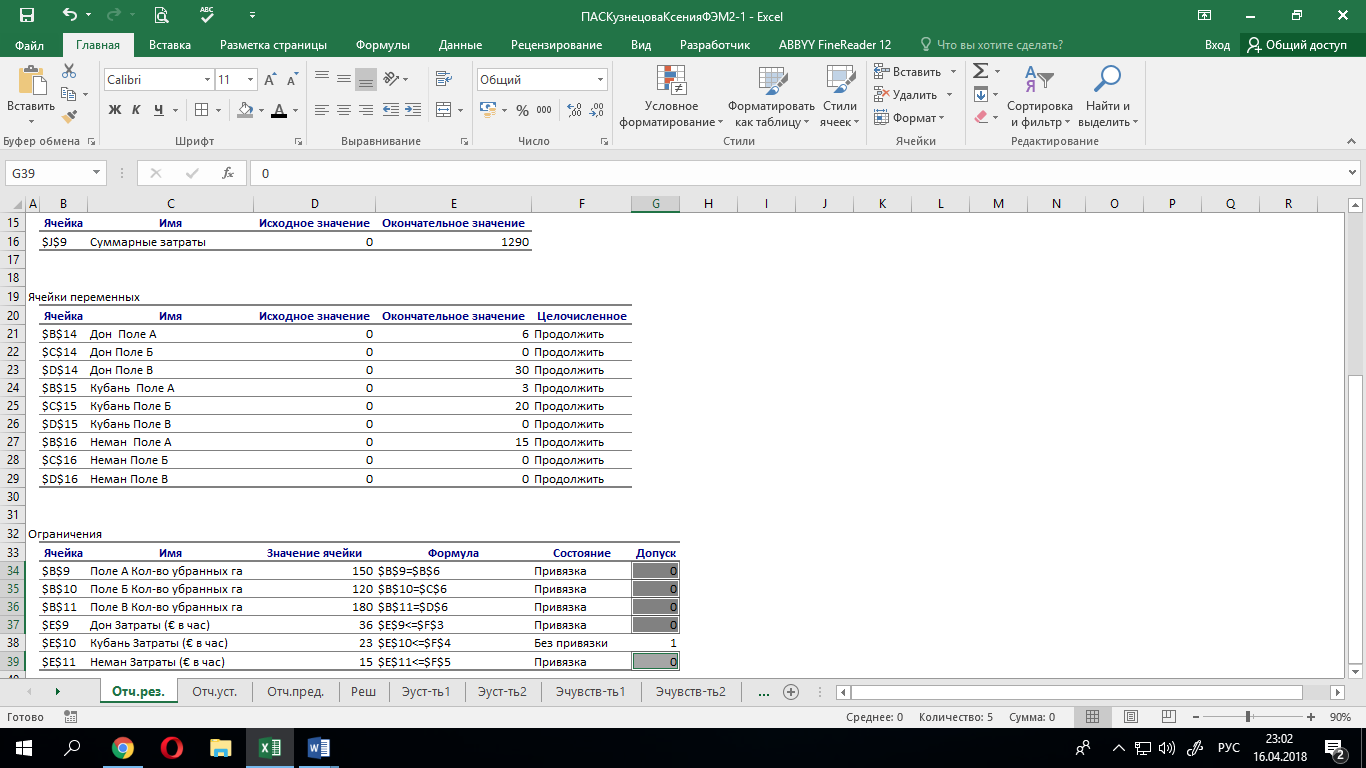Обратимся к отчетам по результатам и устойчивости.В отчете по устойчивости (1.4.2) заметим, что каждому нулевому окончательному значению соответствует ненулевое значение приведённой стоимости (выделено цветом).1.4.2 Отчёт по устойчивости1.4.3 Отчет по результатамТакже, обращаясь к данным отчетам (1.4.2 и 1.4.3), можно сказать, что каждому нулевому допуску для ограничений соответствует ненулевое значение теневой цены (выделено цветом).Исходя из вышесказанного, делаем вывод, что задача имеет единственное решение.1.4.3 Эксперимент 1 (устойчивость)Будем менять целевой коэффициент при 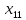(производительность, измеренная в га/час). Допустимый диапазон изменения этого коэффициента – (8,8; 18). Изменим целевой коэффициент с 16 на 17,9. Получим тот же самый оптимальный план: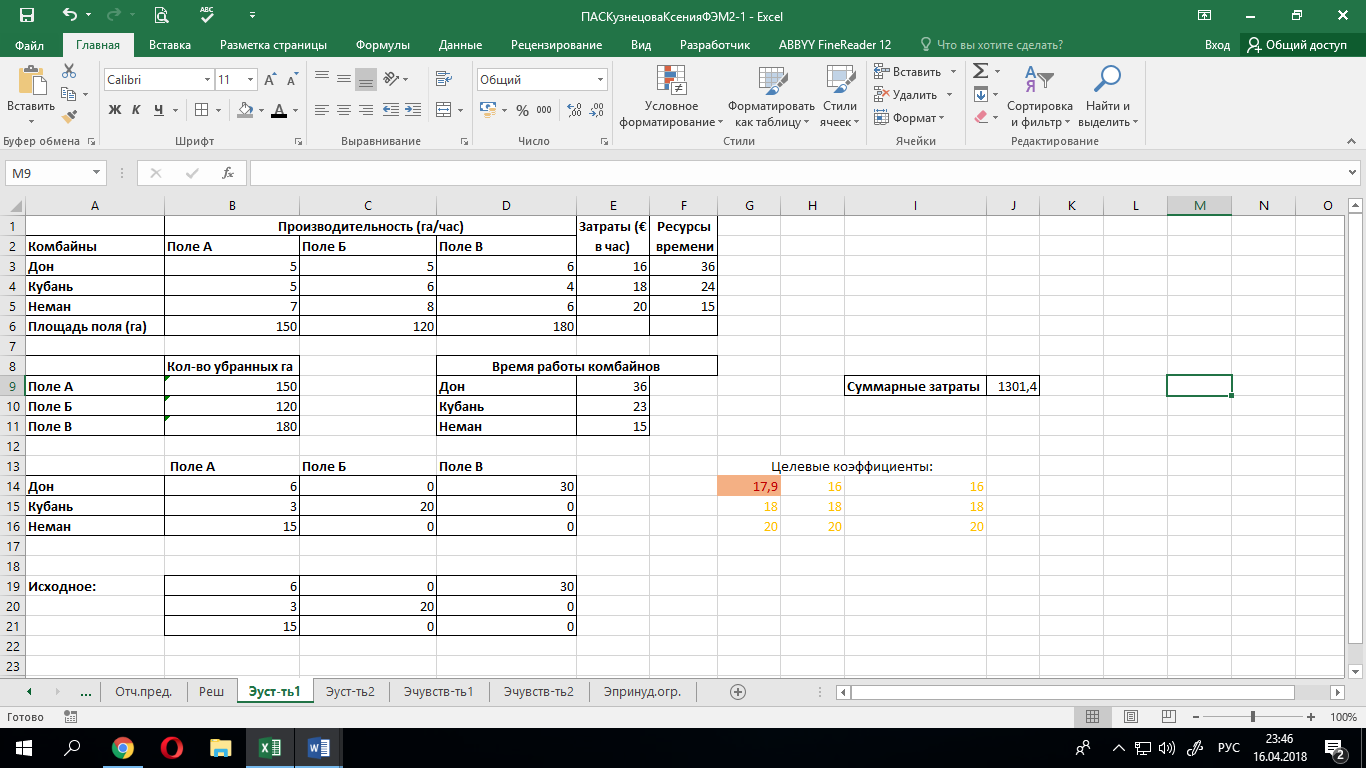При этом целевая функция изменится на величину равную произведению величины изменения коэффициента и окончательного значения соответствующей переменной

---

, т.е.: 1,9*6=11,4. Следовательно значение целевой функции составит: 1290+11,4=1301,4. Что подтверждается экспериментом.
Теперь изменим целевой коэффициент с 17,9 до 18,1, то есть выйдем за пределы допустимого диапазона изменения коэффициента. Получим решение, отличное от исходного. Оптимальный план изменился:


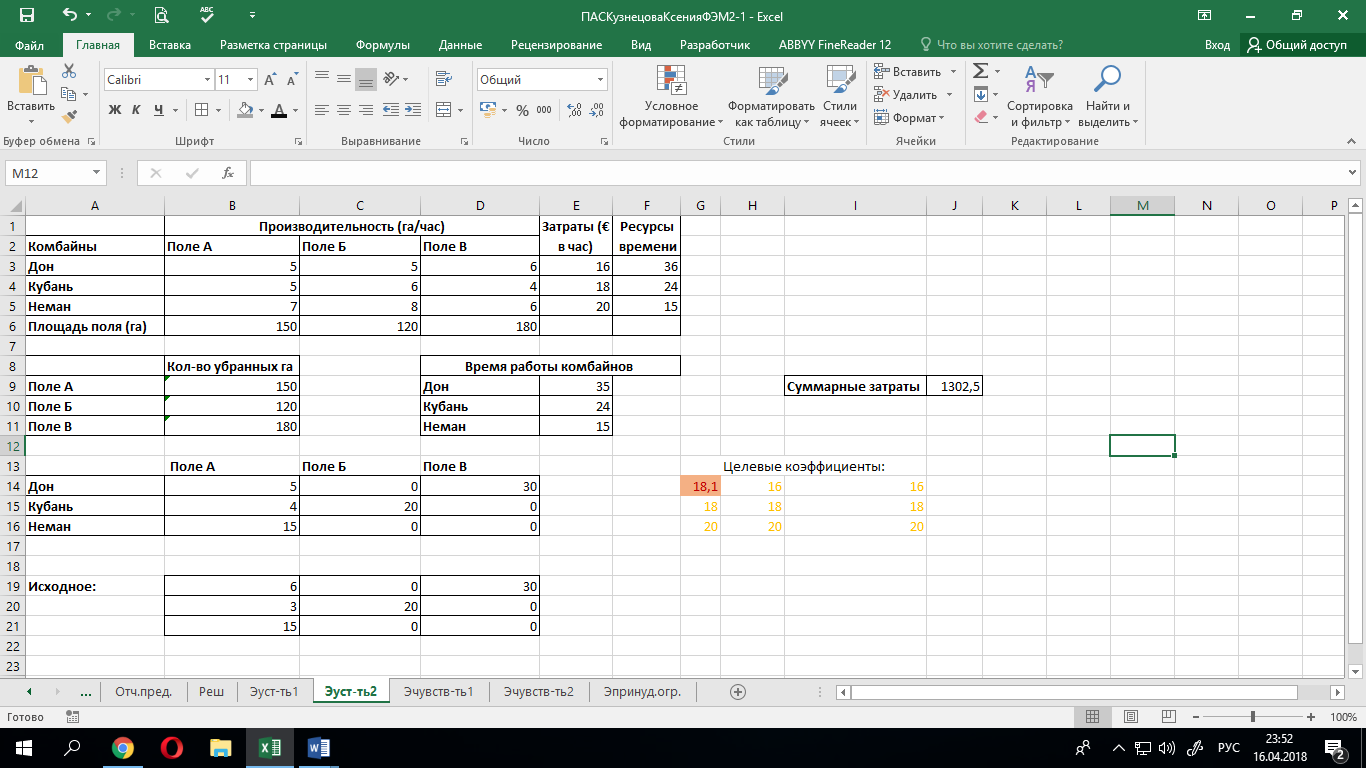
1.4.4 Эксперимент 2 (чувствительность)

Будем менять количество га, которые необходимо убрать на поле А (по условию задачи: 150 га). Допустимый диапазон изменения лежит в интервале (135; 155). Предположим, что нужно убрать 135,1 га. Изменение значения целевой функции составит величину равную произведению значения теневой цены (отчет по устойчивости) на величину изменения, т.е. новое значение целевой функции составит: 1290-14,9*3,6=1236,36. Это подтверждается экспериментом:



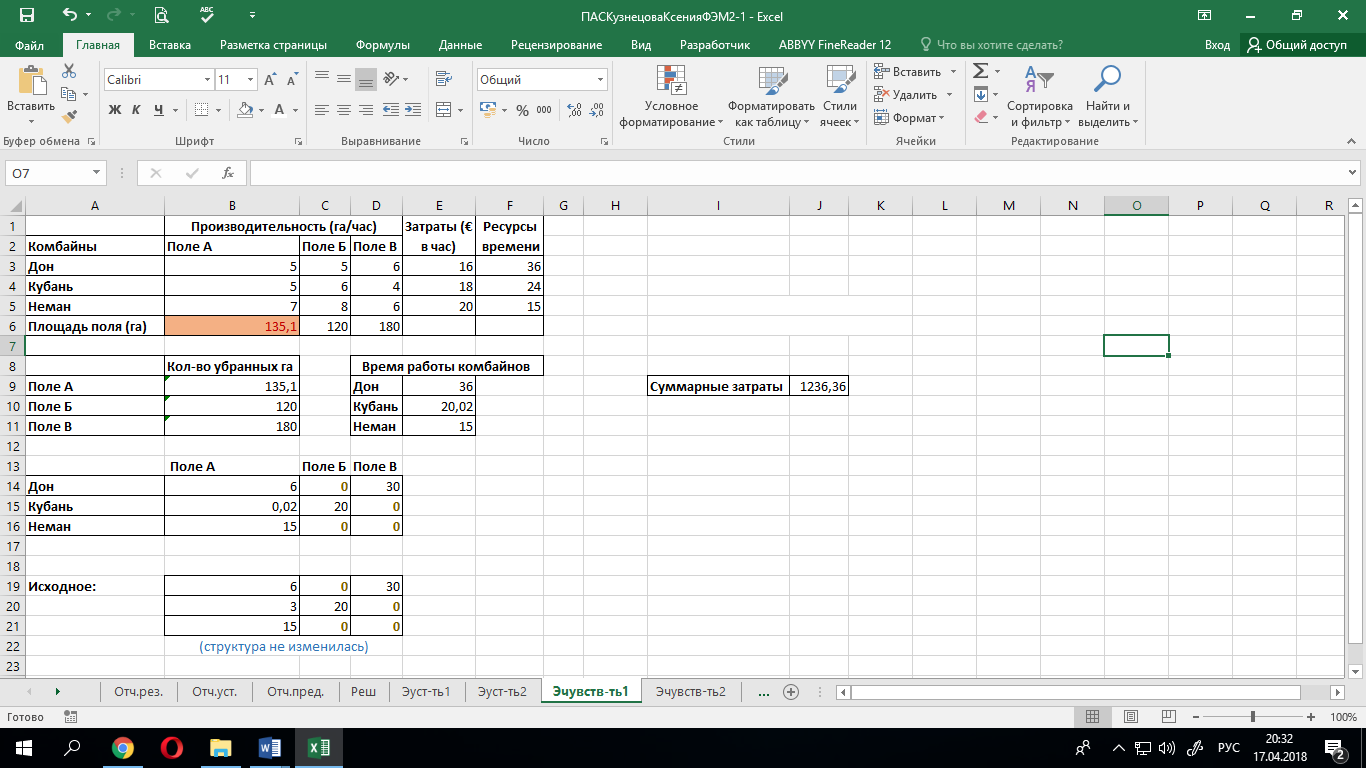
В результате эксперимента оптимальный план изменился, но структура плана не поменялась: соответствующим нулевым компонентам исходной матрицы соответствуют нулевые значения компонент в полученной матрице, а положительным – положительные.

Заметим также, что и структура допусков (значений балансовых переменных) осталась неизменной: положительные допуски остаются положительными, а нулевые допуски – нулевыми.

Исходные значения Значения, полученные в результате эксперимента





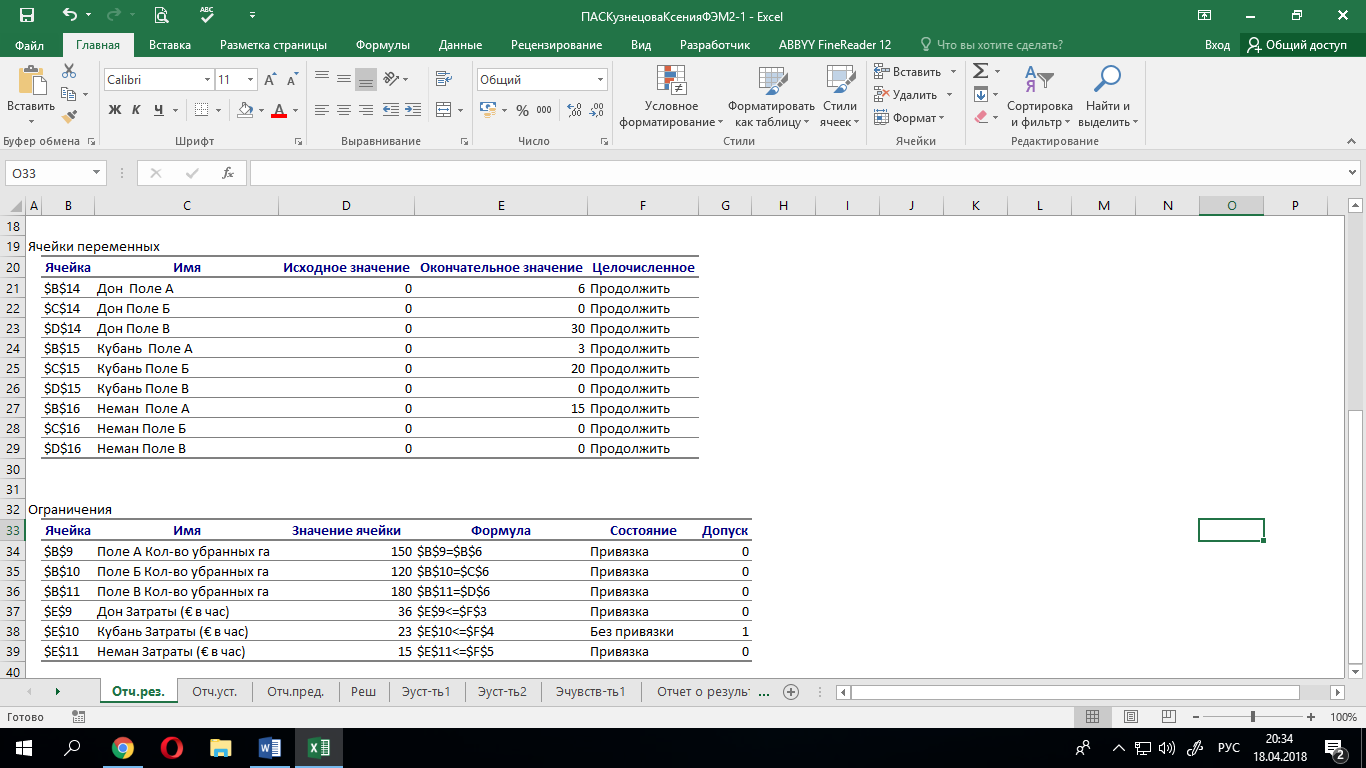
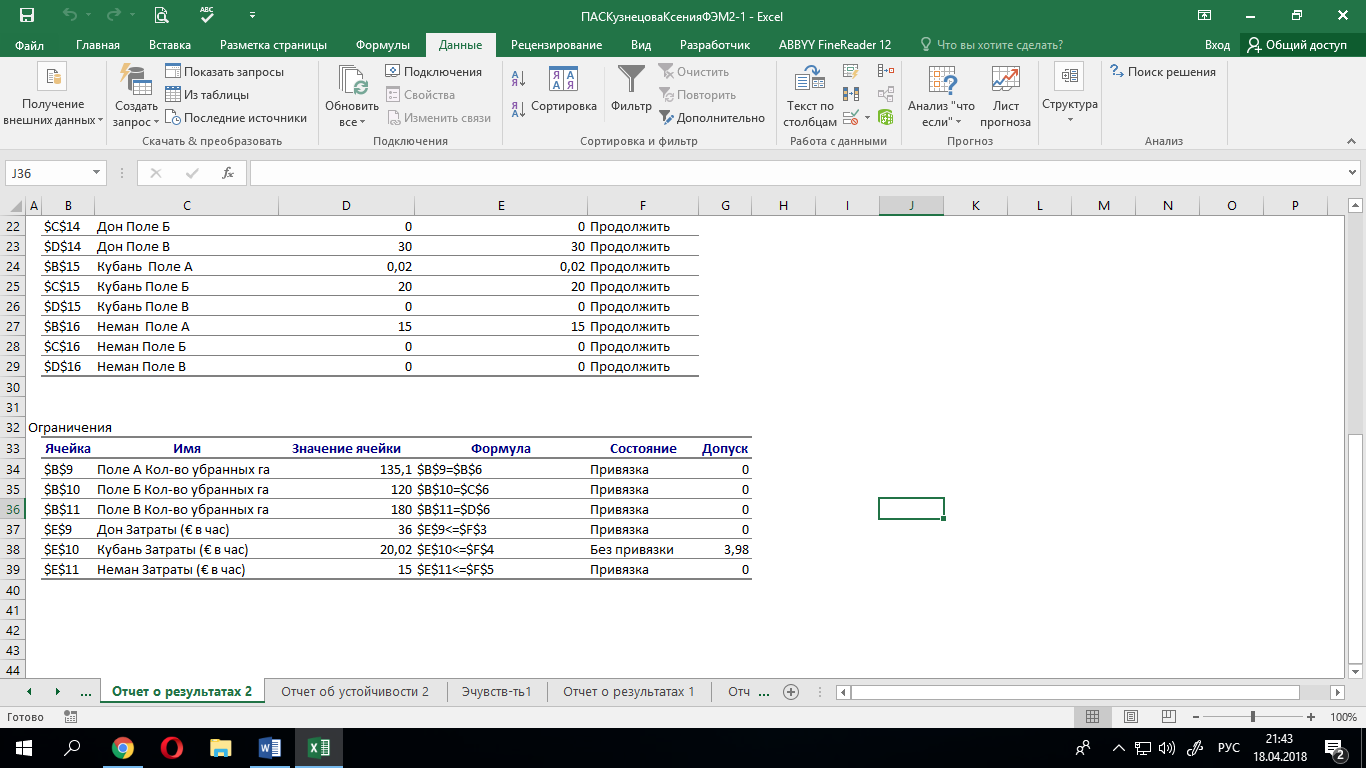
Теперь предположим, что с поля А нужно убрать 134,9 га. Получим следующий результат:



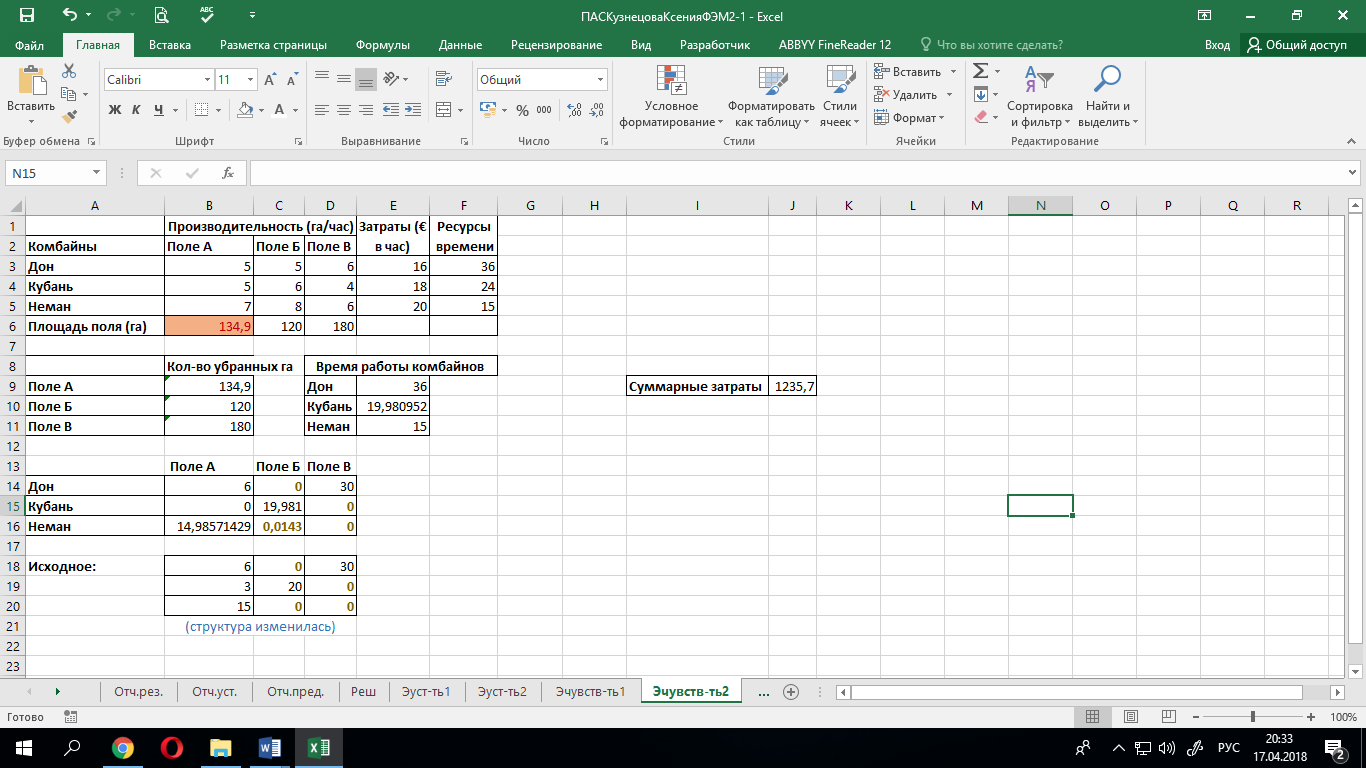
Заметим, что после введения данного ограничения оптимальный план и его структура изменились. В полученной матрице 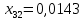, в исходном же решении значение данной переменной было равно 0.

Эксперимент 3 (принудительное ограничение)

---

Зададим следующее условие: время работы комбайна «Неман» на поле Б не должно быть меньше 2 часов, то есть 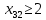. Добавим соответствующее ограничение в список, уже имеющийся в диалоговом окне «Поиска решений». При этом мы можем спрогнозировать изменение оптимального значения целевой функции: оно будет равно произведению значения приведённой стоимости (отчёт 1.4.2) и величины изменения переменной (в нашем случае исходное значение 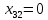, а теперь 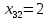, то есть величина составит 2-0=2). Т.е. 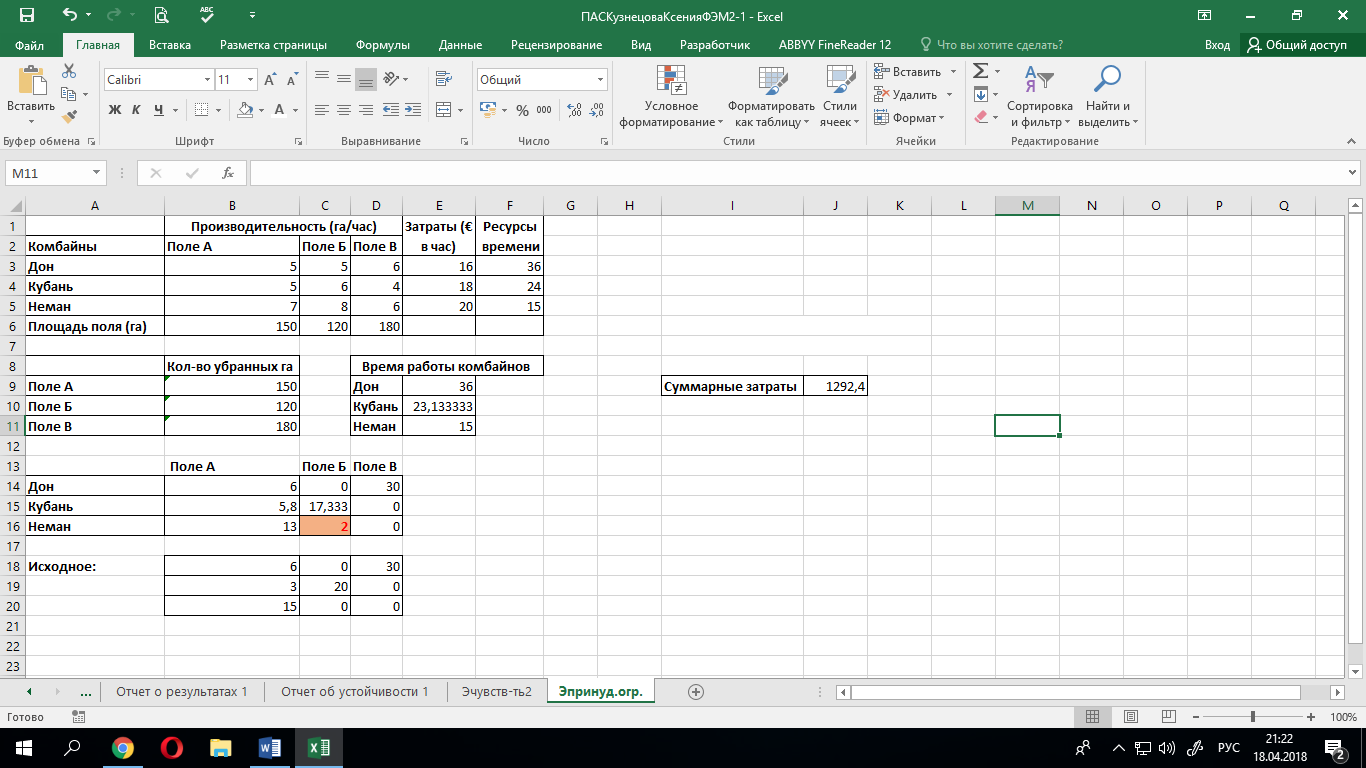новое оптимальное значение целевой функции составит: 1290+2*1,2=1292,4.Получим следующий результат:Наш прогноз подтверждён результатами эксперимента. Имеем новый оптимальный план в соответствии с введённым ограничением.

---

Смотрите также файлы

• Отработка техники дыхательной гимнастики. Тренировка на свежем воздухе.docx

• Курсовая работа получение фурцелларана из водоросли furcellaria lumbricalis 2021 г. Содержание введение 3.docx

• Малімі Рамазанова А. С. Сынып 7 Оытуда олданылатын дістсілдер.doc

• 83 Здоровый образ жизни.docx

• зін зі тану сабаыны жоспары. Мектеп Белгілі Е. Зікібаев атындаы рнек негізгі мектебі.doc