Файл: Голдбах жорамалы былай дейді рбір 2 ден лкен жп сан екі жай санны осындысына жіктеледі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 51
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Голдбах жорамалы былай дейді: әрбір 2 ден үлкен жұп сан екі жай санның қосындысына жіктеледі.
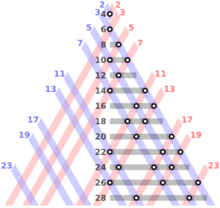
Goldbch partitions
Гольдбах мәселесі – алтыдан үлкен (артық) немесе оған тең кез ө келген бүтін санның – үш жай санның қосындысына тең болуы немесе тең болмауы жайындағы мәселе. Бұлл мәселені 1742 жылы неміс математигі Христиан Гольдбах (1690 – 1764) жариялаған. Жай сандардың өзара көбейту арқылы кез келген санды жазуға болады ал, жай санддарды өзара қосса, бұл жағдайда да қосылғыштар санын қалауыңызға арттыра отырып кез – келген бүтін сан жазуға болады: жұп сандар екі санын қайталап қосу арқылы ал, тақ сандарды ылғи үш сандарын және бірнеше екі санын қайталап қосу арқылы жазуға болады. Христиан Гольдбах тақ сандардың жұбын қосындылаған. Сонда ол мына жайтты байқаған: Әр ретте жұп санды екі тақ санның қосындысы түрінде жазуға болады. Екі таңбалы сандарға арналған әлгі жіктеудің бірқатары мыналар:
4 = 2 + 2,6 = 3 + 3,8 = 3 + 5,10 = 3 + 7 = 5 + 5,12 = 5 + 7,14 = 3 + 11 = 7 + 7,16 = 3 + 13 = 5 + 11,18 = 5 + 13 = 7 + 11,20 = 3 + 17 = 7 + 13;
Осы тұжырым дұрыс екені анық, бірақ, әлі толық дәлелі жоқ. Гольдбах мәселесі - алтыдан үлкен (артық) немесе оған тең кез келген бүтін санның – үш жай санның қосынды тең болуы немесе тең болмауы жайындағы мәселе. Бұл мәселені 1742 жылы неміс математигі Христиан Гольдбах (1690 – 1764) жариялаған. Жай сандарды өзара көбейту арқылы кез келген санды жазуға болады. Ал, жай сандарды өзара қосса не болады? Әрине, мұнда да қосылғыштардың санын қалауымызға арттыра отырып кез келген бүтін сан жазуға болады: жұп сандар 2 санын қайталап қосу арқылы, ал, тақ сандарды ылғи 3 сандарын және бірнеше 2 санын қайталап қосу арқылы жазуға да болады екен. Екі таңбалы сандарға арналған әлгі жіктеудің бірқатары мыналар (Гольдбах заманында 1 саны жай сан деп есептеген):
4=1+3,6=1+5,8=1+7,10=3+7,12=5+7,14=3+11,
16=3+13,18=5+13,20=3+17,22=11+11,24=11+13, 96=89+7,98=97+1, 86=43+43,88=87+1,90=87+3,92=87+5,94=87+7; 1742-ші жылдан бері қарай қаншама математик осы есепті шешіуге тырысқанымен әлі де болса , кереметтей дәлелін таппай келеді.
Гольдбах мәселесін зерттеу кезінде, ең алдымен, 270 жылдан бері көптеген адамдарға тыныштық бермейтін гипотезаны бастаған екі көрнекті математик туралы айту керек.
Біріншіден, бұл мәлімдеме аты аталған
адам туралы айту керек, бұл Кристиан Гольдбах. Гольдбах (1690-1764) көп саяхаттады, негізінен математиктермен танысты және олардың кейбірімен тиімді хат алмасуды қолдады. Берлинде біраз уақыт тұрғаннан кейін, ол 1725 жылы Санкт-Петербургке көшіп келіп, ғылым академиясына мүше, ал көп ұзамай ғылым академиясынның хатшысы болып сайланды. 1742 жылы Сыртқы істер министрлігіне қызметке жіберілді. Мәскеуде қайтыс болды. Оның жоғары математика саласындағы жұмысы толығымен 1729 жылдан 1764 жылға дейін жүргізілген Л.Эйлермен хат алмасулардан белгілі. Осы жалпы хат-хабарлардан Фусс (Эйлердің ұлы) 177 мәтіні "XVIII ғасырдың кейбір белгілі геометрлерінің математикалық және физикалық сәйкестігі" ("Correspondance mathématique et physique de quelques célèbres géomètres du XVIII siècle") I томында басылады.
Екіншіден, Гольдбах проблемасын тұжырымдау мен зерттеуде осы ғылымдардың дамуына іргелі үлес қосқан швейцариялық, неміс және орыс математигі және механигі Леонард Эйлер рөл атқарды. Эйлер 850-ден астам жұмыстың авторы. Эйлер 3000-нан астам хаттары бар белсенді ғылыми хат алмасуды жүргізді.
Бұл жұмыста қарастырылған мәлімдемені алғаш рет 1742 жылы Христиан Гольдбахтың Леонард Эйлерге жазған хатында тұжырымдады, онда Гольдбах келесі болжам жасады:
"5-тен үлкен әрбір тақ санды үш жай санның қосындысы ретінде көрсетуге болады".
Мысалы:
7=2+2+3
9=2+2+5=3+3+3
11=2+2+7=3+3+5
13=3+3+7=3+5+5
15=2+2+11=3+5+7=5+5+5
17=2+2+13=3+3+11=3+7+7=5+5+7
19=3+3+13=3+5+11=5+7+7
21=2+2+17=3+5+13=3+7+11=5+5+11=7+7+7
23=2+2+19=3+3+17=3+7+13=5+5+13=5+7+11
25=3+3+19=3+5+17=3+11+11=5+7+13=7+7+11
Эйлер бұл мәселеге қызығушылық танытып, одан да күштірек болжам жасады:
"Екіден үлкен әрбір жұп санды екі жай санның қосындысы ретінде көрсетуге болады".
Мысалы:
4=2+2
6=3+3
8=3+5
10=3+7=5+5
12=5+7
14=3+11=7+7
16=3+13=5+11
18=5+13=7+11
20=3+17=7+13
22=3+19=5+17=11+11
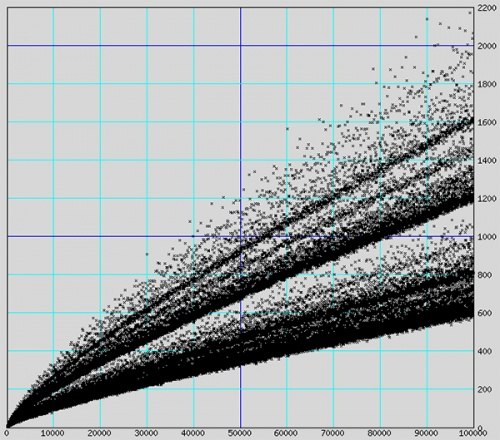
1-суретте "Гольдбах кометасы" деп аталатын график бейнеленген, онда жұп сандарды екі жай санның қосындысы ретінде көрсетудің әртүрлі нұсқаларының саны көрсетілген
2-суретте бірнеше алғашқы жұп сандардың жай сандардың қосындысына схемалық бөлінуі көрсетілген.
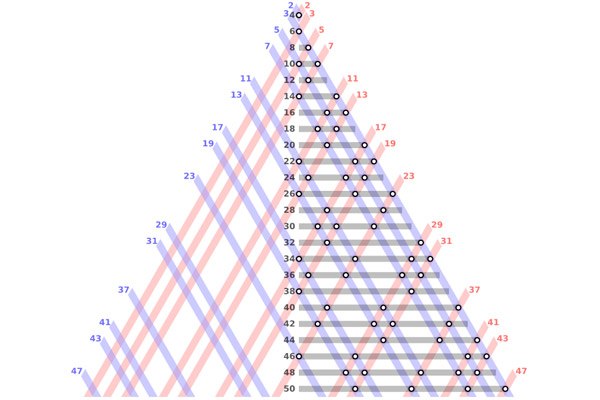
Бірінші мәлімдеме Гольдбахтың тернарлық мәселесі, екіншісі Голдбахтың бинарлық мәселесі (немесе Эйлер мәселесі) деп аталады. Голдбахтың бинарлық мәселесін растау әділдігінен Гольдбахтың тернарлық мәселесінің әділдігі автоматты түрде жүреді: егер 4-тен басталатын әрбір жұп сан екі жай санның қосындысы болса, онда әрбір жұп санға 3 қосу арқылы 7-ден басталатын барлық тақ сандарды алуға болады. Мұндай жағдайларда бинарлық проблемадағы мәлімдеме тернарлыққа қарағанда күшті деп айтылады.
Гольдбах мәселесі (Риман гипотезасымен бірге) Гильберттің мәселелер тізіміне 8 нөмірімен енгізілген. Гильберт мәселелері-1900 жылы Парижде өткен II Халықаралық математиктер конгресінде Дэвид Гильберт ұсынған 23 негізгі математика мәселелерінің тізімі. Ол кезде бұл мәселелер (математика негіздерін, алгебраны, сандар теориясын, геометрияны, топологияны, алгебралық геометрияны, Ли топтарын, нақты және күрделі талдауды, дифференциалдық теңдеулерді, математикалық физика мен ықтималдық теориясын және вариациялық есептеуді қамтитын) шешілмеді. Қазіргі уақытта 23 мәселенің 16-сы шешілді. Тағы 2-уі дұрыс математикалық мәселелер емес (біреуі шешілгенін немесе шешілмегенін түсіну үшін тым түсініксіз тұжырымдалған, екіншісі шешуден алыс-математикалық емес, физикалық). Қалған 5 мәселенің екеуі ешқандай жолмен шешілмеген, ал Гольдбах мәселесі өз кезегінде Гильберттің дербес жағдайларда ғана шешілген үш мәселесінің бірі болып табылады.
Жоғарыда айтылғандардың бәрінен көріп отырғанымыздай, Гольдбах проблемасының тұжырымы, тернарлы немесе бинарлы болсын, өте қарапайым және қол жетімді, тіпті қарапайым орта мектеп оқушысы үшін де. Дегенмен, оның толық дәлелі әлі жоқ, бұл Гольдбах мәселесін оның шешімін табуға тырысатын әуесқой математиктер арасында да, жалпы әлемдік мәдениетте де өте танымал етеді. 270 жылдан бері адамдар Христиан Гольдбахтың мәлімдемесін дәлелдеуге тырысып келеді, әрі қарай гольдбахтың проблемасын дәлелдеуде неге қол жеткізілгені туралы айтылады.
Риман тұжырымдамасы
Гольдбах мәселесін одан әрі қарастыру үшін Риман гипотезасы деп аталатын негізгі ұғымдарды белгілеу керек. Айта кету керек, бұл гипотезаның әділдігі туралы болжамнан Гольдбахтың тернарлы проблемасының дәлелі құрылды, сондықтан төменде келтірілген мәселеге ерекше назар аудару керек.
Сонымен, Риманның Зета функциясының нөлдерінің таралуы туралы Риман гипотезасын 1859 жылы Бернхард Риман тұжырымдады. Натурал сандар арасында жай сандардың таралуын сипаттайтын ешқандай заңдылық табылмағанымен, Риман x — тен аспайтын жай сандардың саны — π(x) деп аталатын жай сандардың таралу функциясы-дзета функциясының "тривиальды емес нөлдері" деп аталатын үлестіру арқылы өрнектелетінін анықтады.
Жай сандардың таралуы туралы көптеген мәлімдемелер, соның ішінде кейбір бүтін алгоритмдердің есептеу күрделілігі Риман гипотезасының дұрыстығын болжауда дәлелденген.
Риман гипотезасы жеті "мыңжылдық мәселелерінің" тізіміне енеді, олардың әрқайсысын шешу үшін Клэй математикалық институты (Clay Mathematics Institute, Кембридж, Массачусетс) миллион АҚШ доллары көлемінде сыйақы төлейді. Бұл тұжырымның күрделілігі соншалық, Гильберт тіпті 500 жылдан кейін ұйықтап, оянса, бірінші кезекте Риманның гипотезасы дәлелденген-дәлелденбегенін сұрайды деп әзілдеді. Риман гипотезасына қарсы мысал жарияланған жағдайда, Клэй институтының Ғылыми кеңесі бұл қарсы мысалды мәселенің түпкілікті шешімі деп санауға болатындығын немесе мәселені неғұрлым тар түрде қайта құрып, ашық қалдыруға болатындығын шешуге құқылы (соңғы жағдайда, қарсы мысалдың авторына сыйақының аз бөлігі төленуі мүмкін).
Гипотеза келесідей тұжырымдалған:
ς(S) Риманның дзета функциясы барлық күрделі комплекс S≠1 сандар үшін анықталған және теріс жұп S=-2, -4, -6… нөлдері бар.
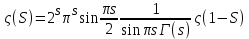функционалдық теңдеуден және 
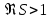кезіндегі 
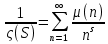айқын өрнегінен, мұндағы 
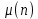— Мобиус функциясы, "тривиальды емес" деп аталатын барлық басқа нөлдер 
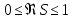жолағында "критикалық сызық" деп аталатын 
, 
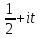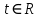сызыққа симметриялы түрде орналасқаны шығады.Риман гипотезасы мынаны айтады:
Зета функциясының барлық тривиальды емес нөлдері 1/2-ге тең нақты бөлікке ие.
Басқа, теориялық және сандық тұжырымдау жиі қолданылады:
Келесі асимптотикалық формула жай сандарды бөлу үшін дұрыс па:
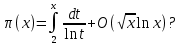
Шолу жұмыстарында (Bombieri 2000, Conrey 2003, Server 2008) Риман гипотезасының ақиқаттығын қолдайтын деректер күшті, бірақ негіздеме күмән тудыратын орын қалдыратынын атап өтті. Алайда жекелеген авторлар гипотезаның жалғандығына сенімді (атап айтқанда, Джон Литлвуд осылай ойлады).
Гипотезаның ақиқатын болжайтын мәліметтердің ішінде бастапқы гипотезалардың сәтті дәлелдерін бөліп көрсетуге болады. Бұл Риман шарты автоморфтық карталарға қатысты барлық Зета функциялары үшін орындалады деген ең күшті теориялық дәлел, бұл Риманның классикалық гипотезасын қамтиды. Осыған ұқсас гипотезаның ақиқаты Селбергтің Зета функциясы үшін, кейбір жағынан Риманға ұқсас және госсанепиднадзордың Зета функциясы үшін дәлелденген.
Екінші жағынан, Эпштейннің кейбір Зета функциялары Риман шартын қанағаттандырмайды, дегенмен олардың сыни сызықта шексіз нөлдері бар. Алайда, бұл функциялар Эйлер қатарлары арқылы көрсетілмейді және автоморфтық карталармен тікелей байланысты емес.
Риман гипотезасының ақиқатының пайдасына "практикалық" дәлелдерге zetagrid(таратылған есептеу саласындағы ең ірі жобалардың бірі) жобасы шеңберінде Зета функциясының тривиальды емес нөлдерінің көп санын есептеу тексерісі жатады. Қалай болғанда да, Риман гипотезасы әлі күнге дейін жалпы және толық шешімге ие емес. Осыған қарамастан, оның ақиқаты сандар теориясының басқа теоремаларын, атап айтқанда голдбах мәселесін дәлелдеу кезінде жиі қабылданады.
Гольдбахтың тернарлы мәселесі.
Бұрын айтқанымыздай, голдбахтың екі түрлі тұжырымы бар тернарлы және бинарлы, төменде біз тернарлы мәселені қарастырамыз.
Тернарлы проблема-бұл Гольдбахтың бинарлы ("күшті") проблемасының ақиқаты болып табылатын әлсіз мәлімдеме.
ХХ ғасырдың басында Гольдбах гипотезалары Риман гипотезасымен бірге сандар теориясының орталық міндеттерінің біріне айналды, тіпті Гильберттің әйгілі 8-ші проблемасының бөлігі болды.
Бұл мәселені шешудегі жетістікті Британдық математиктер Гарольд Харди мен Джон Литтлвуд жасады. Содан кейін олар Варинг мәселесін зерттеді. 1916-1917 жылдардағы жұмыстарға енген Харди мен Сиривас Раманужанның идеяларын дамыта отырып, Британдық математиктер дөңгелек әдіс деп аталатын әдісті жасады. Оның мәні келесідей: есепті шешу (мысалы, бүтін санды үш жайдың қосындысы ретінде көрсету тәсілдерінің саны) белгілі бір қатардан бірлік шеңбер бойынша интегралмен беріледі. Бұл интеграл екіге бөлінеді, олардың біреуі бағаланады, ал екіншісі туралы оның салыстырмалы түрде аздығы дәлелденеді. Бірінші қосынды құраушылар үлкен доғалар, ал екіншісі кіші доғалар деп аталады.
Перу математигі Харальд Хельфготт (бұл сәл кейінірек талқыланады) бұл әдісті былай сипаттады: "шешімдердің санын талдау негізінен Фурье түрлендіру арқылы жүзеге асырылады. Елестетіп көріңізші, жай сандар — бұл кейбір жазбалардағы дыбыстар, айталық, 2, 3, 5, 7, 11 және т.б. микросекундтар. Түрлендіруден кейін сіз қандай да бір ноталарды естуге тырысатын Шу түрін аласыз. Олардың арасында жақсы естілетіндер бар-бұл үлкен доғалар. Шу фрагменттері болып табылатын жиіліктер бар — бұл шағын доғалар. Бүкіл әдіс екі бөлікке бөлінеді — ноталарды бөлектеу және қалғанының Шу екенін дәлелдеу. Әдістің бірінші бөлігі үшін бағалау үлкен доғаларға, екіншісі кіші доғаларға жауап береді".