Файл: Голдбах жорамалы былай дейді рбір 2 ден лкен жп сан екі жай санны осындысына жіктеледі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Олардың әдісін қолдана отырып, Харди мен Литтлвуд Гольдбахтың тернарлы гипотезасын дәлелдей алды. Алайда олардың дәлелдемелерінде бір, бірақ өте маңызды кемшілік болды, ол іс жүзінде барлық жұмысты кесіп өтті: мақалада олар Риманның дәлелденбеген жалпыланған гипотезасына сүйенді.
1937 жылы Харди мен Литтлвуд әдісін Иван Матвеевич Виноградов (кеңестік математик, КСРО Ғылым Академиясының академигі) жетілдірді, ол Риман гипотезасының әділдігіне тәуелді емес дәлелдер келтірді, яғни кез-келген жеткілікті үлкен тақ санды үш жай санның қосындысы ретінде ұсынуға болатындығын дәлелдеді.
Әңгімені жалғастырмас бұрын, біз маңызды шегініс жасаймыз. Осы сәттен бастап (яғни 1937 жылдан бастап) кеңестік математиктер мен оларға достық қарым-қатынас Гольдбахтың тернарлы мәселесін шешті деп санайды, ал шетелдік математиктер бұған келіспейді. Өкінішке орай, шетелдіктер дұрыс айтады: Виноградов ерекше жұмыс жасағанына қарамастан, мәселе түпкілікті шешілмеді. Виноградовтың шешімін толық және түпкілікті деп атауға болмайды, өйткені ол бұл "жеткілікті үлкен санға"нақты баға берген жоқ. Содан бері көптеген математиктер Виноградовтың нәтижесін жақсартуға тырысты. Осы әрекеттердің барлығының идеясы өте қарапайым болды: бағалауды жақсарту арқылы N-нің аз болуына қол жеткізу. Бұл жағдайда "жеткілікті кішкентай" деген мағынаны білдіреді, ол үшін Гольдбах гипотезасын компьютерде тексеруге болады. 1989 жылы Ванг пен Чен төменгі бетін
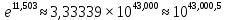деңгейіне дейін түсірді, бұл қазіргі заманғы есептеу техникасының дамуындағы барлық кіші сандарды нақты тексеру үшін әлі де қол жетімді емес.Дегенмен, И.М. Виноградовтың Гольдбах мәселесін шешуге де, жалпы математикаға да қосқан үлесі орасан зор. Гольдбах мәселесін шешуге тырысқанда, ғалым сандар теориясының ең жалпы және қуатты әдістерінің бірін — тригонометриялық қосындылар әдісін жасады, бұл аналитикалық сандар теориясының көптеген мәселелері
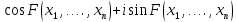, мұндағы 
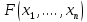- нақты бүтін функция. Бұл әдісті қолдана отырып, ол өзі және оның ізбасарлары сандар теориясында да, математиканың басқа салаларында да көптеген керемет нәтижелерге қол жеткізді.2012 жылы әйгілі сандар теориясының маманы және 2006 жылғы Филдс медалінің иегері Терренс Таоның жұмысы жарық көргенге дейін голдбах мәселесін шешуде 20 жылға жуық уақыт болған жоқ. Ол кез-келген тақ санның бес жай саннан аспайтын қосынды ретінде ұсынылатындығын көрсете алды.
2013 жылдың мамыр айының ортасында қазіргі уақытта Францияда жұмыс істейтін Перу математигі Харальд Хельфготт Корнелл университетінің алдын ала басып шығару мұрағатына "Голдбах теоремасына арналған үлкен доғалар"мақаласын жариялады. Бұл мақалада голдбахтың үштік проблемасының соңғы дәлелі бар.
"Мен голдбах мәселесімен 2006 жылы айналыса бастадым", — деді Хельфготт. — Мен сол кездегі шағын доғаларды бағалауды жақсарта алатынымды тез түсіндім. Бұл жұмыстың нәтижесі деп аталатындар болды логарифмсіз бағалау (мен бұл нәтижелерді тез алдым). Әрі қарай жұмыс әлдеқайда баяу жүрді-өйткені мен бағалауды сандық жағынан ғана емес, сапалық жағынан да жақсартуға тырыстым. Басынан бастап мен бұл тапсырманы сапалы жақсартусыз алға жылжу мүмкін емес сияқты сезіндім".
Хельфготтың еңбектерінің нәтижесі барлық қажетті бағаларды қамтитын 133 беттік жұмыс болды. Негізгі теорема келесідей: 1029-дан үлкен Барлық тақ бүтін сандар үш жай санның қосындысы ретінде ұсынылуы мүмкін. Бұрын голдбах гипотезасының талабы (Хельфготтың өзі Дэвид Блаттпен бірлесе отырып) 8,875 x 1030 дейін тексерілген. Бұл екі факт бірге голдбахтың үштік гипотезасының нақты дәлелі болып табылады. Бір қызығы, жаңа жұмыс тағы бір жерде сандық әдістерге сүйенеді: дәлелдеу үшін тамырлардың жеткілікті саны үшін Риманның жоғарыда айтылған жалпыланған гипотезасын тексеру керек болды. Мұны Дэвид Платт жасады.
Гольдбахтың бинарлы мәселесі.
Естеріңізге сала кетейік, биннарлы мәселе келесі тұжырымға ие:
Екіден үлкен әрбір жұп санды екі жай санның қосындысы ретінде көрсетуге болады.
Гольдбахтың бинарлы мәселесі әлі шешілмейді. Бинарлы мәселе үшін дөңгелек әдіс жұмыс істемейді-ондағы кішкентай доғалардың әсері тым күшті.
Виноградов 1937 жылы және Теодор Бестерман 1938 жылы жұп сандардың барлығы дерлік екі жай санның қосындысы ретінде ұсынылатындығын көрсетті (егер бар болса, елестетілмейтіндердің үлесі нөлге ұмтылады). Бұл нәтижені 1975 жылы Хью Монтгомери мен Роберт Чарльз Свон аздап күшейтті. Олар екі жай санның қосындысы ретінде ұсынылмайтын
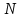-ден Үлкен емес жұп сандардың саны 
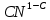аспайтындай оң 
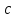және 
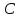тұрақтылары бар екенін көрсетті.1930 жылы Лев Шнирельман кез - келген жұп сан қарапайым саннан аспайтын мөлшерде ұсынылатындығын көрсетті, мұндағы
-белгілі бір тұрақты. Бастапқыда бұл өте үлкен болды: 1969 жылы кеңестік математик Климов саны 6 000 000 000-нан аспайтынын көрсетті. Бұл нәтиже бірнеше рет жақсартылды-1995 жылы Оливер Рамаре кез-келген жұп санның алтыдан аспайтын мөлшерде ұсынылатындығын көрсетті. Хельфготтың жаңа нәтижесі Рамаренің нәтижесін жақсартуға мүмкіндік беретіні назар аудартады: жұп саннан үштікті алып тастағанда, біз тақ санды аламыз, ол қазір үш жайдың қосындысы ретінде ұсынылатыны белгілі. Мүмкін, кез-келген жұп сан төрт жай санның қосындысы түрінде ұсынылатын шығар. Гольдбахтың тернарлы гипотезасының әділдігінен (2013 жылы дәлелденген) кез — келген жұп сан 4 жай саннан аспайтын сома болып табылады.Математиктердің өздері Гольдбахтың күшті мәселесін шешу әлі алыс деп санайды.