Российский государственный социальный университет

ИТОГОВОЕ ПРАКТИЧЕСКОЕ ЗАДАНИЕ

по дисциплине «Экономика»

ФИО студента	Гусейнова Айгюн Илгар кызы
Направление подготовки	Сестринское дело
Группа	СЕД-Б-01-В-2020-2

Москва 2020

Задание №1

На основе теории спроса и предложения проанализируйте и объясните следующие ситуации:

1. 
   Почему в периоды наибольшего потребления цена на одни блага, например фрукты, падает, а на другие блага, например гостиничные номера в причерноморских отелях, возрастает?
   

2. 
   Почему, узнав о повышении цен на кожу, руководство компании, владеющей сетью обувных магазинов, распорядилось уволить часть продавцов?
   

3. 
   Осенью спрос на шерстяные варежки вырос, однако их цена осталась на том же уровне, что и весной. Как изменилась за это время цена на шерсть?
   

4. 
   Подорожал сахар. Через полгода цена на мороженое оказалась на том же уровне, что и накануне подорожания. Зимой или летом подорожал сахар, если рассматривать его как единственное сырье, чья цена изменялась в течение рассматриваемого промежутка времени?
   

Решение:

а) Изменение цен в периоды наибольшего потребления может быть обусловлено изменением спроса на блага или изменением предложения благ; в данном случае:

- периодом наибольшее потребления фруктов является осень, когда созревает новый урожай, следовательно возрастает предложение фруктов (а согласно теории спроса и предложения, увеличение предложения при прочих равных условиях, обуславливает эффект снижения цен — новое равновесное состояние между спросом и предложением устанавливается при более низкой цене, чем ранее);

---

- периодом наибольшего потребления гостиничных услуг в причерноморских отелях является лето, когда наступает время массовых отпусков, следовательно, возрастает спрос на гостиничные номера (а согласно теории спроса и предложения, увеличение спроса при прочих равных условиях, вызывает эффект роста цен — новое равновесное состояние между спросом и предложением устанавливается при более высокой цене, чем ранее).

b) Согласно теории спроса и предложения, рост цены на ресурсы (в данном случае кожа является материальным ресурсом при производстве обуви) снижает доступность ресурсов, что в свою очередь, является фактором, обуславливающим снижение предложения на товары, производимые из этих ресурсов (в данном случае — обуви). Поэтому закономерно, что ожидая снижение поставок и объемов продаж обуви, руководство компании увольняет часть продавцов, т. к. реализацию меньшего объема обуви можно осуществить с меньшим количеством продавцов.

с) Согласно теории спроса и предложения, рост спроса на определенный товар (в данном случае — шерстяные варежки) при прочих равных условиях ведет к повышению цены, но если цена осталась на том же уровне, значит существует какое-то условие, которое обусловило эту устойчивость цены. Таким условием может является снижение цены на ресурсы (т. к. шерсть является материальным ресурсом при производстве варежек), что и служит фактором, обуславливающим рост предложения на товары, производимые из этих ресурсов (варежек). Таким образом, рост спроса на варежки был уравновешен ростом предложения варежек, поэтому и цена на варежки осталась на том же уровне.

d) Согласно теории спроса и предложения, рост цены на ресурсы (в данном случае сахар является материальным ресурсом при производстве мороженного) снижает доступность ресурсов, что в свою очередь, является фактором, ведущим к снижению предложения товаров, производимых из этих ресурсов (в данном случае — мороженного). При прочих равных условиях это должно было бы вызвать рост цен на мороженное, но если цена осталась на том же уровне, значит существует какое-то условие, которое обусловило эту устойчивость цены. Таким условием может быть снижение спроса на товар, что служит фактором, обуславливающим снижение цены этого товара (в данном случае — мороженного). Таким образом, снижение предложения мороженного было уравновешено снижением спроса на мороженное, поэтому и цена на мороженное осталась на том же уровне.

---

Так как снижение спроса на мороженное происходит зимой (когда на улице холодно), то временем подорожания сахара (полгода назад) является лето.

Ответы: а) цена на фрукты снизилась из-за роста предложения, цена на гостиничные номера увеличилась из-за роста спроса на них; b) рост цен на кожу обусловил снижение предложения (т.е. меньшие объемы реализации) обуви, что и ведет к сокращению численности продавцов; с) цена на шерсть снизилась; d) рост цен на сахар произошел летом.

Задание №2

Владелец фирмы «Папа и сын», являющейся монополистом на рынке некоторого товара, хочет максимизировать прибыль от производственной деятельности. Известны функции спроса и переменных затрат фирмы: Qd = 160 – 0,5P (Qd — величина спроса на товар в тыс. ед., Р — цена товара в рублях), VC = 20Q + Q² (Q — количество произведенной продукции в тыс. ед., VС — переменные издержки в рублях). По совету своего сына, изучавшего недавно в школе экономику, владелец назначил такую цену, при которой эластичность спроса по цене равнялась –1. «Что-то там точно максимально», — сказал сын своему отцу. В результате прибыль составила 1,8 млн р. Во сколько раз оказалась бы больше прибыль монополиста, если бы сын владельца фирмы лучше учился в школе и дал верный совет своему отцу?

Решение:

1) Определим цену продукции, которую установил отец по совету своего сына.

Для расчета цены используем формулу эластичности спроса, выраженную линейным уравнением, и модель функции спроса с использованием коэффициентов:

модель функции спроса: Q(P) = а - bР, 

уравнение эластичности спроса: Е = bР / Q,

где Q — объем продаж; Р — цена единицы товара; Е -эластичность спроса по цене;a и b – коэффициенты функции спроса

В данном случае коэффициенты равны: а = 160, b = -0,5, следовательно:

Е = bР / Q = -0,5 * Р / (160 – 0,5P) = -1 → -0,5Р = - 160 + 0,5Р

0,5Р + 0,5Р = 160 → Р = 160 руб.

2) Рассчитаем объем продаж при цене, которую установил отец по совету своего сына:

Q_d = 160 – 0,5P = 160 — 0,5 * 160 = 80 тыс. шт.

3) Определим выручку от реализации (TR), полученную отцом по совету своего сына:

TR = Q * P = 160 * 80 = 12 800 тыс. руб.

4) Определим величину общих затрат (ТС), как разницу между полученной выручкой от реализации (TR) и полученной прибылью (РR):

ТС = TR - РR = 12 800 — 1 800 = 11 000 тыс. руб.

5) Рассчитаем величину постоянных затрат (FС), исходя из общих затрат и функции переменных затрат (для объема продаж 80 тыс.шт. при цене 160 руб.):

---

FС = ТС — VC = 11 000 - (20Q + Q²) = 11 000 – (20 * 80 + 80²) = 3 000 тыс. руб.

6) Согласно правилу максимизации прибыли, действующем практически на любом рынке, максимальная прибыль достигается, когда величина предельного дохода (MR) равна величине предельных издержек (MC):

MR = MC

6.1) Предварительно выразим цену продукции через функцию спроса:

Q = 160 – 0,5P → 0,5P = 160 – Q → P = 320 – 2Q

6.2) Рассчитаем предельный доход как производную от функции выручки и предельные издержки как производную от функции общих затрат:

MR = ТR` = (P * Q)` = ((320 – 2Q)Q)` = (320Q – 2Q<sup>2</sup>)` = 320 – 4Q

МС = ТС` = (FC + VC)` = (3000 + 20Q + Q²)` = 20 + 2Q

6.3) Найдем оптимальный объем продаж, при котором прибыль максимальна:

MR = MC → 320 – 4Q = 20 + 2Q

6Q = 320 – 20 → Q = 300/6 = 50 тыс. руб.

6.4) Определим цену продукции, при которой прибыль максимальна:

P = 320 – 2Q = 320 — 2 * 50 = 220 руб.

6.5) Рассчитаем выручку от реализации, при которой прибыль максимальна:

TR = Q * P = 50 * 220 = 11 000 тыс. руб.

6.6) Рассчитаем общие затраты для объема продаж, при котором прибыль максимальна:

ТС = FС + VC = 3000 + 20Q + Q² = 3000 + 20 * 50 + 50² = 6 500 тыс. руб.

6.7) Определим максимальную прибыль:

РR = TR – ТС = 11 000 — 6 500 = 4 500 тыс. руб.

6.8) Определим превышение максимально возможной прибыли (рассчитанной исходя из условия максимизации прибыли) над фактически полученной прибылью:

∆РR = 4500 / 1 800 = 2,5 раза

Ответ: прибыль была бы больше в 2,5 раза

Задание №3

В ателье по ремонту бытовой техники работают четыре человека. До уплаты подоходного налога годовой заработок каждого составляет: у Маши — 60 тыс. р.; у Павла — 72 тыс. р.; у Дмитрия — 120 тыс. р.; у Максима — 120 тыс. р. В соответствии с Налоговым кодексом Российской Федерации все работники ателье уплачивают подоходный налог по ставке 13%.

1. 
   Постройте кривую Лоренца до уплаты подоходного налога для данного ателье.
   

2. 
   Становится ли распределение доходов более равномерным после уплаты подоходного налога? Ваш вывод подтвердите соответствующими расчетами.
   

Решение:

a) Построим кривую Лоренца до уплаты подоходного налога.

1) Предварительно рассчитаем общий годовой заработок (ΣЗП) всех четырех человек, исходя из годового заработка каждого работника (Зп_i):

ΣЗП = ΣЗП_i = 60 + 72 + 120 + 120 = 372 тыс. руб.

2) Найдем доли индивидов (d_i) в общем доходе:

d_i = Зп_i / ΣЗП * 100

---

d = 60 / 372 * 100 = 16,13% (доля Маши в общем доходе)

d = 72 / 372 * 100 = 19,35% (доля Павла в общем доходе)

d = 120 / 372 * 100 = 32,26% (доля Дмитрия в общем доходе)

d = 120 / 372 * 100 = 32,26% (доля Максима в общем доходе)

3) Для построения кривой Лоренца определим кумулятивные (накопленные) доли доходов и численности индивидов, начав с самого бедного, и постепенно включая более богатых индивидов:

3.1) Доля дохода Маши — 16,13%, тогда суммарная доля доходов Маши и Павла:

16,13 + 19,35 = 35,48 %

Суммарная доля доходов Маши, Павла и Дмитрия (либо Максима):

35,48 + 32,26 = 67,74 %

Суммарная доля доходов Маши, Павла, Дмитрия и Максима:

67,74 + 32,26 = 100%

3.2) Доля численности каждого индивида:

1 человек / 4 человека * 100 = 25%

Доля численности Маши — 25%, тогда суммарная доля численности Маши и Павла:

25 + 25 = 50 %

Суммарная доля численности Маши, Павла и Дмитрия (либо Максима):

50 + 25 = 75 %

Суммарная доля численности Маши, Павла, Дмитрия и Максима:

75 + 25 = 100%

Построим кривую Лоренца (рис.1) по значениям кумулятивных (накопленных) долей доходов и численности населения:



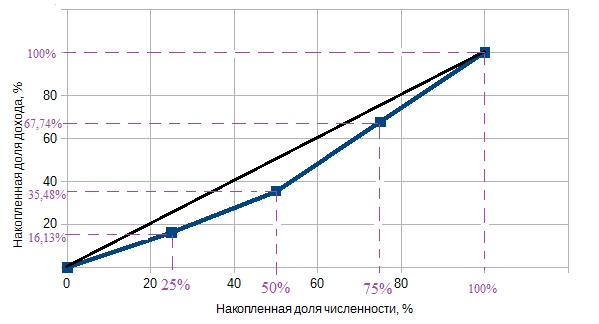
Рис.1 Кривая Лоренца до уплаты подоходного налога

Прямая линия, соединяющая левую нижнюю точку и правую верхнюю точку графика, называется линией равномерного распределения доходов. Это гипотетическая линия, которая показывает, что было бы, если бы доходы распределялись равномерно.

b) Определим становится ли распределение доходов более равномерным после уплаты подоходного налога.

1) Рассчитаем суммы доходов после уплаты подоходного налога по ставке 13%.

Доход Маши = 60 — 13% = 52,2 тыс. руб.;

Доход Павла = 72 — 13% = 62,64 тыс. руб.;

Доход Дмитрия = 120 — 13% = 104,4 тыс. руб.;

Доход Максима = 120 — 13% = 104,4 тыс. руб.;

2) Рассчитаем общий годовой заработок (ΣЗП) всех четырех человек после уплаты налога:

ΣЗП = ΣЗП_i = 52,2 + 62,64 + 104,4 + 104,4 = 323,64 тыс. руб.

3) Найдем доли индивидов (d_i) в общем доходе после уплаты налога:

d_i = Зп_i / ΣЗП * 100

d = 52,2 / 323,64 * 100 = 16,13% (доля Маши в общем доходе)

d = 62,64 / 323,64 * 100 = 19,35% (доля Павла в общем доходе)

d = 104,4 / 323,64 * 100 = 32,26% (доля Дмитрия в общем доходе)

d = 104,4 / 323,64 * 100 = 32,26% (доля Максима в общем доходе)

4) Так как доли индивидов в общем доходе после уплаты подоходного налога остались без изменения, то и кумулятивные (накопленные) доли доходов останутся без изменений

---

Смотрите также файлы

• Боевой подготовки подразделений сухопутных войск.doc

• Институт сферы обслуживания и предпринимательства (филиал) федерального государственного бюджетного образовательного учреждения высшего образования донской государственный технический университет в г. Шахты ростовской области.docx

• Виды заданий егэ, связанных с изучением причастий.pptx

• Группа заболевания Упражнения рекомендованные.docx

• Задача Требование лицензирующего органа правомерно, так как содержащие врачебную тайну документы затребованы им в рамках контроля качества и безопасности медицинской деятельности.docx