Добавлен: 12.12.2023
Просмотров: 87
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Муниципальное образовательное учреждение
«Средняя общеобразовательная школа №43»
города Твери
Тема проекта: «Симметрия вокруг нас».
Тип проекта: информационный.
Проектный продукт: реферат.
Выполнил:
ученик 8 «Г» класса
Лебедев Артем Дмитриевич
Научный руководитель:
Карпова Елена Владимировна
Тверь 2019
Содержание
Введение…………………………………………………………3
Глава 1. История появления термина «симметрия»…….……4
Глава 2. Симметрия в геометрии………………………………6
Глава 3. Типы симметрии……………………………………….8
3.1 Осевая симметрия…………………………………………...8
3.2 Центральная симметрия…………………………………….10
3.3 Зеркальная симметрия………………………………………11
3.4 Вращательная симметрия…………………………………..12
3.5 Винтовая симметрия……………………………………….13
3.6 Скользящая симметрия…………………………………….15
Глава 4. Применение симметрии……………………………16
Заключение…………………………………………………....20
Список использованной литературы………………………..22
Введение
Люди всегда видели симметрию в окружающем их мире и восхищались ей. Они замечали, как прекрасны тела людей, животных, растений; снежинки, кристаллы…, а ведь все эти творения природы, так или иначе, отвечают законам симметрии. Сложился один из главных принципов красоты – то, что симметрично – красиво. Тогда люди стали использовать симметрию в скульптуре и архитектуре, в написании букв своих алфавитов, стремясь отразить это симметричное великолепие природы. И вот, на симметрию обратили внимание ученые.
«Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту, совершенство.»,-пишет Герман Вейль.
«…быть прекрасным значит быть симметричным и соразмерным.»,говорит древнегреческий философ Платон.
Сейчас симметрия играет огромную роль в жизни человечества. Симметрия используется во множестве областей нашей жизни (в науке, технике, искусстве и т.д.). Огромное количество научных гипотез, законов, теорий строится на принципах симметрии, а также она активно используется в различных отраслях строительства и техники (например, при проектировании и конструировании архитектурных сооружений и оформлении фасадов зданий).
Но все это пришло к нам не сразу. Сначала понадобились сотни лет, чтобы изучить симметрию, прежде чем она нашла такое широкое применение в жизни людей. Изучением симметрии занимается такая наука, как геометрия. Именно симметрия в геометрии позволяет людям сейчас использовать это понятие в совершенно различных областях жизнедеятельности человечества.
Тема симметрии в геометрии очень актуальна в наше время, и я заинтересовался этим вопросом, что побудило меня создать данную работу.
Цель моей работы: применение знаний о симметрии в различных областях жизни людей.
Для достижения поставленной цели мне необходимо решить следующие задачи:
1.Познакомиться с историей появления термина «симметрия»
2.Выяснить, что такое симметрия в геометрии
3.Узнать, какие типы симметрии в геометрии существуют
4.Узнать, как применяются геометрические знания о симметрии.
Глава 1
История появления термина «симметрия».
Представители первой научной школы в истории человечества, последователи Пифагора Самосского, пытались связать симметрию с числом. Каждой вещи, учили пифагорейцы, соответствует определенное отношение чисел, которое они называли логосом. Пифагорейцы предпочитали вместо слова «симметрии» пользоваться словом «гармония». Широко используя идею гармонии и симметрии, ученые древности любили обращаться не только к сферическим формам, но и к правильным многогранникам. У правильных многогранников грани – правильные многоугольники одного вида, а углы между гранями равны. Древние греки установили, что с
уществует всего пять правильных выпуклых многогранников, название которых связаны с числом граней, - тетраэдр, октаэдр, икосаэдр, куб, додекаэдр. Все правильные многогранники обладают зеркальной симметрией.Познавательную силу симметрии оценили философы Древней Греции, используя ее в своих натурфилософских теориях. Так, например, Анаксимандр из Милета, живший в первой половине VI в. до н. э., использовал симметрию в своей космологической теории, где в центре мира поместил Землю — главное, по его мнению, тело мира. Она должна была иметь совершенную, симметричную форму, форму цилиндра. Земля расположена точно в центре, и здесь симметрия имеет смысл равновесия.
Весы известны человеку с III в. до н. э. В состоянии равновесия массы грузов на разных концах коромысла одинаковы — положение коромысла симметрично относительно центра тяжести. Симметрия — это не только равновесие
, но и покой: стоит добавить на одну из чашек весов дополнительный груз, как они придут в движение. Нарушено равновесие, исчезла симметрия — появилось движение.Гармония (симметрия) состоит из противоположностей. В пространственной симметрии противоположности явно видны.
И Леонардо да Винчи не обошел своим вниманием симметрию. Он рассмотрел равновесие шара, имеющего опору в центре тяжести: две симметричныеполовины шара уравновешивают друг друга и шар не падает. Как художник он главное внимание уделял изучению законов перспективы и пропорций, с помощью которых выявляются художественные достоинства произведений искусства.
У древних народов Атлантиды, как стало известно учёным по найденным рукописям термин «симметрия» означал совершенство, а по найденным фигуркам, статуэткам и другим вещам, стало ясно, что в древней Атлантиде было всё строго симметрично.
В науку симметрия вошла в 30-х гг. XIX в. в связи с открытием Гесселем32 кристаллографических классов и появлением теории групп как области чистой математики. Кристаллы наделены наибольшей величиной симметрии из всех реальных объектов. Симметричной в кристаллографии считается фигура, которая делится без остатка на равные и одинаково расположенные части.
Законы природы являются симметричными, но при ближайшем их рассмотрении, в каждом из них можно найти хоть небольшой изъян. Оказывается, что природа не терпит точной симметрии. Природа почти, но не абсолютно симметрична. Примером этому является например человек – внешне он симметричен, но строение органов и их расположение абсолютно ассиметрично.
Таким образом понятие «симметрия» известно с глубокой древности.
Глава 2
«Симметрия» в геометрии.
В геометрии «симметрия» определяется как свойство геометрических фигур. Именно геометрическая «симметрия» наиболее известна людям, так как она легко различима невооруженным глазом.
Если после какого-либо геометрического преобразования она сохранит определенные исходные свойства-то такая геометрическая фигура симметрична.
Например, если мы повернем квадрат вокруг своего центра на 900, то его форма и размер останутся неизменными .
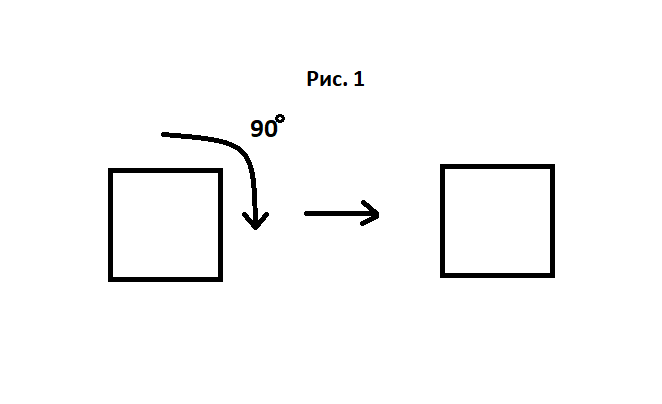
Рис.1
На рисунке 1, можно увидеть, как преобразовался квадрат. Он сохранил свои исходные свойства, следовательно, его можно назвать симметричным относительно вращения.
Вообще, симметрия в геометрии разделяется на шесть типов: осевая симметрия, центральная симметрия, зеркальная симметрия, вращательная симметрия, скользящая симметрия и винтовая симметрия.Типы симметрии для данного геометрического объекта определяются возможными геометрическими преобразованиями и свойствами, которые должны остаться неизменными после выполнения геометрических преобразований объекта.
Глава 3
Типы «симметрии»
Давайте рассмотрим несколько видов симметрии:
Осевая симметрия
Первым типом симметрии, который выделяют в геометрии является осевая. Сущность ее заключается в следующем.
Точки А и А1 называются симметричными относительно прямойа (оси симметрии), если отрезок АА1 перпендикулярен прямой а, и прямая а проходит через середину отрезка АА1. (рис.2а)
Фигура называется симметричной относительно прямойа (оси симметрии), если для каждой точки фигуры симметричная ей точка относительно прямойа также принадлежит этой фигуре. Это значит, что фигура обладает осевой симметрией. (рис.2б)
Рис.2а Рис.2б
Этот тип симметрии наиболее популярен в природе. Так, например, живые организмы, в том числе и люди, обладают осевой симметрией, а иногда даже не одной. (Рис.3)
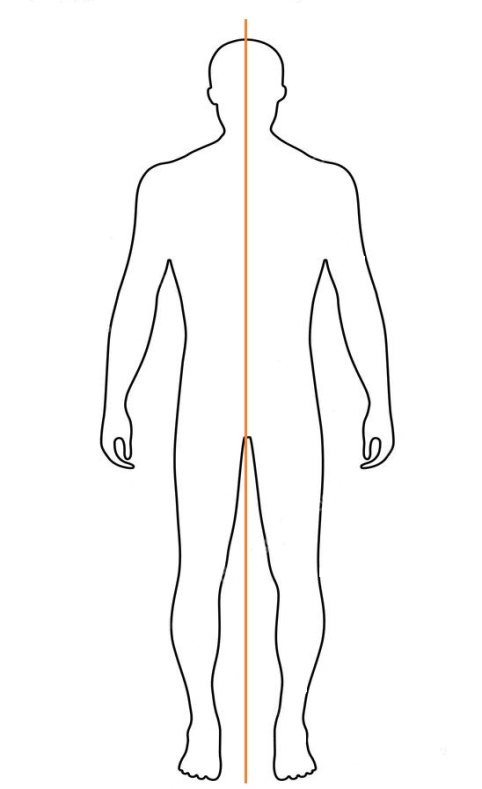
Рис.3. Осевая симметрия в
теле человека
Центральная симметрия
Она выражается в том, что точки А и А1называются симметричными относительно точки О (центра симметрии), если точка О является серединой отрезка АА1. (Рис.4а)
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительноОпринадлежит этой фигуре. В таком случае точка О называется центром симметрии фигуры. Это значит, что фигура обладает центром симметрии. (Рис.4б)
Рис.4а Рис.4б
В повседневной жизни мы очень часто сталкиваемся с этим типом симметрии, однако редко обращаем на него внимание. Достаточно просто посмотреть на настенные часы у которых имеется центральная симметрия. (Рис.5)
Также некоторые животные имеют центральную симметрию. Один из самых красивых примеров-морская звезда. (Рис.6)
Рис.5. Симметрия в Рис.6. Симметрия в теле морской
часах звезды
Зеркальная симметрия
Она определяется следующим образом: точкиА и А1 называются симметричными относительно плоскости S, если плоскость Sделит отрезок АА1 пополам и перпендикулярна к нему. (Рис.7а)
Фигура называется симметричной относительно плоскости S, если для каждой точки этой фигуры симметричная ей точка относительно плоскости S также принадлежит этой фигуре. (Рис.7б)
Рис.7а Рис.7б
Зеркальный тип симметрии также можно встретить и в нашей жизни. Пример такой «отражающей» плоскости – обыкновенное зеркало. (Рис.8).
Рис.8. Отражение в зеркале
Вращательная симметрия
Этот тип симметрии означает, что геометрический объект симметричен относительно определенных вращений этого объекта.
То есть, объект можно назвать симметричным относительно вращения, если при определенном вращении этого объекта он сохранит определенные исходные свойства.
Ранее уже был приведен пример вращательной симметрии, когда речь шла о том, что квадрат никак не изменит исходные размеры и форму при повороте на900. (рис.10)
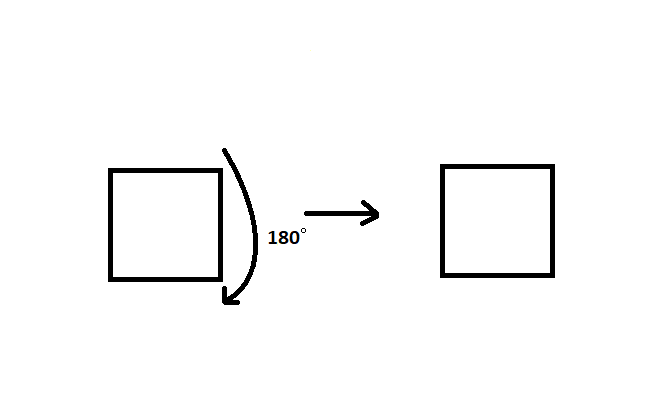
Рис.10
Те же преобразования можно провести с другими объектами (рис.11)
Рис.11
Даже крошечные снежинки, регулируются законами симметрии, так как большинство снежинок имеет вращательную симметрию. (Рис.12)
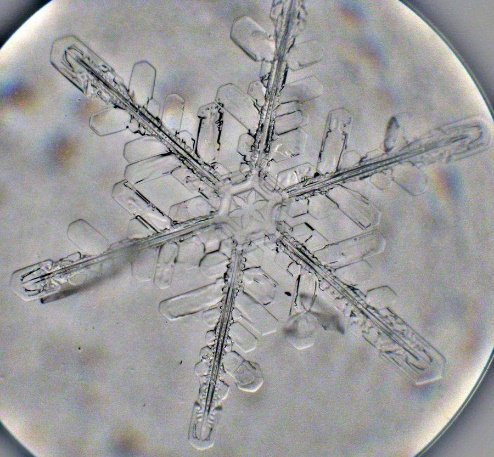
Р
ис.12. Снежинка
Винтовая симметрия
Винтовая симметрия это комплекс преобразований геометрического объекта, в котором одновременно выполняются поворот объекта относительно оси винта и параллельный перенос этого объекта вдоль оси винта. (Рис.13)