2. Моделирование

Практические работы

6. 
   Моделирование работы процессора

1. 
   Напишите программу, которая моделирует работу процессора. Процессор имеет 4 регистра, они обозначаются R0, R1, R2 и R3. Все команды состоят из трех десятичных цифр: код операции, номер первого регистра и номер второго регистра (или число от 0 до 9). Коды команд и примеры их использования приведены в таблице:
   

Код операции	Описание	Пример	Псевдокод
1	запись константы	128	R2 := 8
2	копирование значения	203	R3 := R0
3	сложение	331	R1 := R1 + R3
4	вычитание	431	R1 := R1 – R3

Обратите внимание, что результат записывается во второй регистр. Команды вводятся последовательно как символьные строки. После ввода каждой строки программа показывает значения всех регистров.

2. 
   *Добавьте в систему команд умножение, деление и логические операции c регистрами – «И», «ИЛИ», «исключающее ИЛИ».
   
3. 
   *Добавьте в систему команд логическую операцию «НЕ». Подумайте, как можно использовать второй регистр.
   
4. 
   *Сделайте так, чтобы в команде с кодом 1 можно было использовать шестнадцатеричные значения констант (0-9, A-F).
   
5. 
   Добавьте обработку ошибок типа «неверная команда», «неверный номер регистра», «деление на ноль».
   
6. 
   *Добавьте команду «СТОП», которая прекращает работу программы. Введите строковый массив, моделирующий память, и запишите в него программу – последовательность команд. Ваша программа должна последовательно выполнять эти команды, выбирая их из «памяти», пока не встретится команда «СТОП».
   
7. 
   **Подумайте, как можно было бы организовать условный переход: перейти на N байт вперед (или назад), если результат последней операции – ноль.
   

---

6. 
   Моделирование движения

1. 
   Парашютист массой 90 кг разгоняется в свободном падении до скорости 10 м/с и на высоте 50 м раскрывает парашют, площадь которого 55 м². Коэффициент сопротивления парашюта равен 0,9. Выполните следующие задания:
   

• 
  постройте графики изменения скорости и высоты полета в течение первых 4 секунд;
  
• 
  определите, с какой скоростью приземлится парашютист?
  
• 
  сравните результаты моделирования с установившимся значением скорости, вычисленным теоретически.
  

	теоретически	моделирование
Скорость приземления, м/с

2. 
   Напишите программу, которая моделирует полет мяча, брошенного вертикально вверх, при
   

мм, г, м/с, с.Остальные необходимые данные есть в тексте § 9. Выполните следующие задания:

• 
  определите время полета, максимальную высоту подъема мяча и скорость в момент приземления;
  
• 
  вычислите время полета и максимальную высоту подъема мяча, используя модель движения без сопротивления воздуха:
  

• 
  сравните эти результаты с полученными при моделировании с учетом сопротивления;
  

  	без учёта сопротивления	с учётом сопротивления
  Время полета, с
  Максимальная высота, м
  Скорость приземления, м/с

• 
  можно ли в этой задаче пренебречь сопротивлением воздуха? почему?
  

Ответ

---

:

• 
  с помощью табличного процессора постройте траекторию движения мяча, а также графики изменения скорости, ускорения и силы сопротивления;
  
• 
  уменьшите шаг до 0,01 с и повторите моделирование; сделайте выводы по поводу выбора шага в данной задаче.
  

Ответ:

3. 
   *Выполните моделирование движения мяча, брошенного под углом 45° к горизонту:
   

• 
  определите время полета, максимальную высоту и дальность полета мяча, скорость в момент приземления;
  

  	без учёта сопротивления	с учётом сопротивления
  Время полета, с
  Максимальная высота, м
  Дальность полета, м
  Скорость приземления, м/с

• 
  сравните результаты со случаем, когда сопротивление воздуха не учитывается; сделайте выводы.
  

Ответ:

6. 
   Моделирование популяции животных

Для выполнения работы откройте файл-заготовку Популяция.xls.

1. 
   Постройте графики изменения численности популяции животных для моделей ограниченного и неограниченного роста пр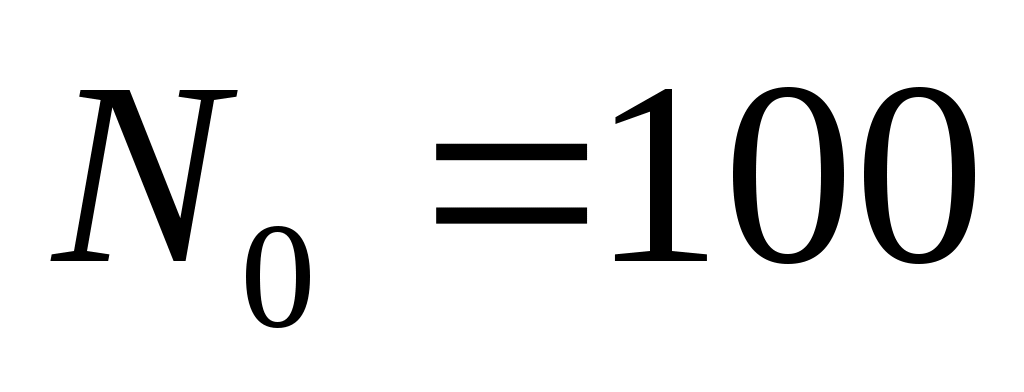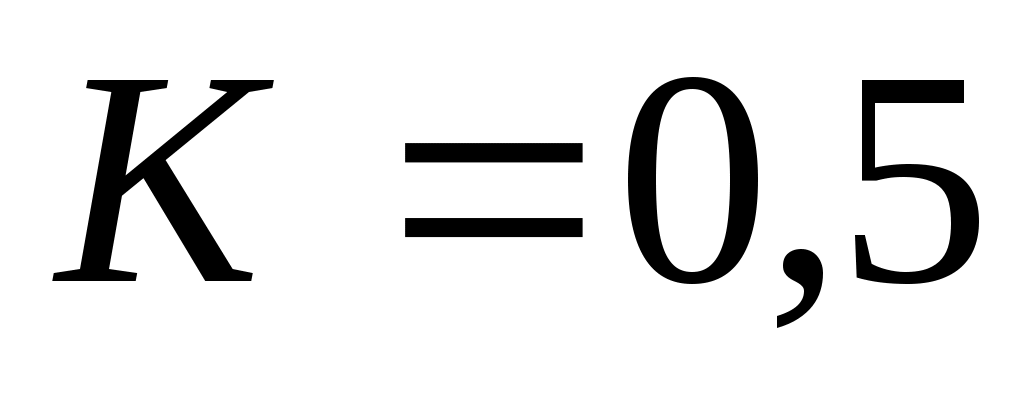и , и 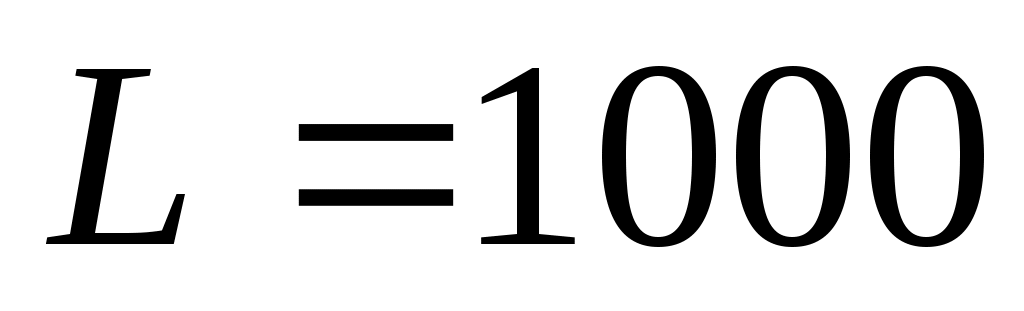в течение первых 15 периодов. Определите, когда модель неограниченного роста перестает быть адекватной (отклонение от модели ограниченного роста составляет более 10%).
   

Ответ:

2. 
   Используя подбор параметра, определите, при каких коэффициентах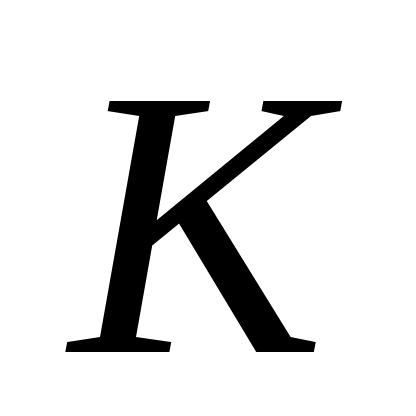 модель неограниченного роста остается адекватной в течение не менее 10 периодов.
   

Ответ:

3. 
   Используя модель ограниченного роста из предыдущей задачи, выполните моделирование популяции с учетом отлова (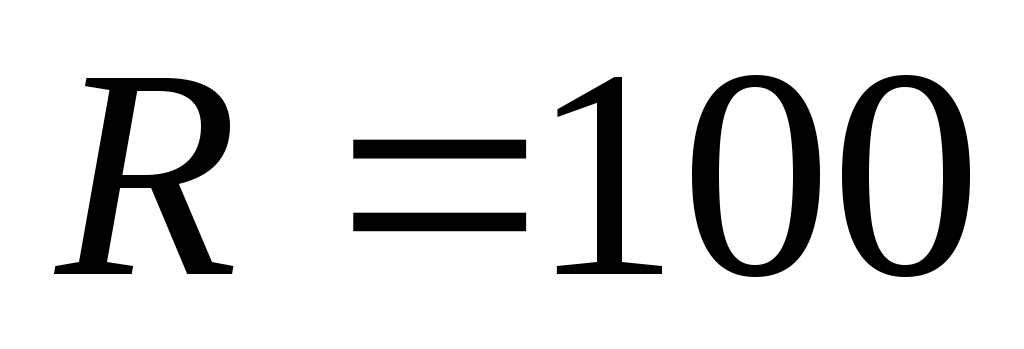 ). Предполагается, что животных начали отлавливать через 10 лет после начала наблюдений.
   

---

• 
  постройте график изменения численности животных;
  
• 
  определите количество животных в состоянии равновесия по результатам моделирования; зависит ли оно от начальной численности?
  

Ответ:

• 
  определите количество животных в состоянии равновесия теоретически, из модели ограниченного роста с отловом; сравните это значение с результатами моделирования
  

Ответ:

• 
  определите, на что влияет начальная численность животных;
  

Ответ:

• 
  определите (по результатам моделирования) максимальный отлов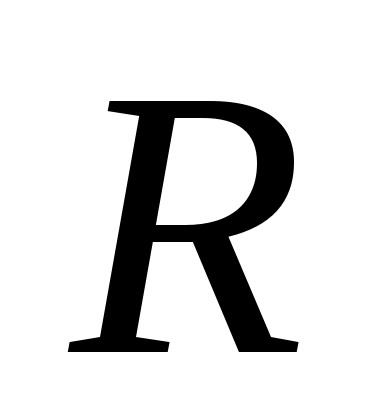 , при котором популяция не вымирает.
  

Ответ:

• 
  *определите максимально допустимый отлов теоретически, из модели ограниченного роста с отловом; сравните это значение с результатами моделирования
  

Ответ:

6. 
   Моделирование эпидемии

Для выполнения работы откройте файл-заготовку Эпидемия.xls.При эпидемии гриппа число больных изменяется по формуле ,где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста: ,где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет): .Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.

---

Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.Ответьте на следующие вопросы:

1. 
   Когда закончится эпидемия?
   

Ответ:

2. 
   Сколько человек переболеет, а сколько вообще не заболеет гриппом?
   

Ответ:

3. 
   Каково максимальное число больных в один день?
   

Ответ:

4. 
   Изменяя коэффициент , определите, при каких значениях модель явно перестает быть адекватной.
   

Ответ:

5. 
   *Сравните модель, использованную в этой работе, со следующей моделью:
   

, .Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?Ответ:Сравните поведение двух моделей при , и . Сделайте выводы.Ответ:

6. 
   Модель «хищник-жертва»

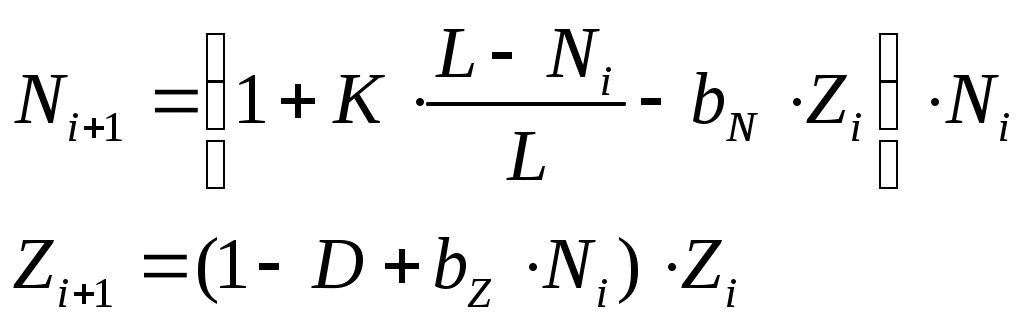
Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.Выполните моделирование биологической системы «щуки-караси»где – численность карасей – численность щукпри следующих значениях параметров: – коэффициент прироста карасей; – предельная численность карасей;

---

Смотрите также файлы

• Ано дпо "волгоградская гуманитарная академия профессиональной подготовки специалистов социальной сферы" Программа профессиональной переподготовки.rtf

• Выполнение практических заданий по дисциплине документирование управленческой деятельности.docx

• Утверждаю начальник 108 пч огпс выборгского района гку Леноблпожспас.doc

• История россии xix века в произведении м. Ю. Лермонтова бородино.docx

• Взаимное усиление действия препаратов при одномоментном применении называется.docx