Файл: Моделирование работы процессора.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 117

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

– начальная численность карасей;

– начальная численность щук;

– коэффициент смертности щук без пищи;

и – коэффициенты модели.

Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.

Ответьте на следующие вопросы:

  1. Сколько карасей и щук живут в водоеме в состоянии равновесия?

Ответ:

  1. Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?

Ответ:

  1. На что влияет начальная численность хищников и жертв?

Ответ:

  1. Подберите значения коэффициентов, при которых модель становится неадекватна.

Ответ:

  1. Подберите значения коэффициентов, при которых щуки вымирают, а численность карасей достигает предельно возможного значения. Как вы можете объяснить это с точки зрения биологии?

Ответ:

Практическая работа № 10а.

Модель «две популяции»


Для выполнения работы откройте файл-заготовку ДвеПопуляции.xls.

Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид:



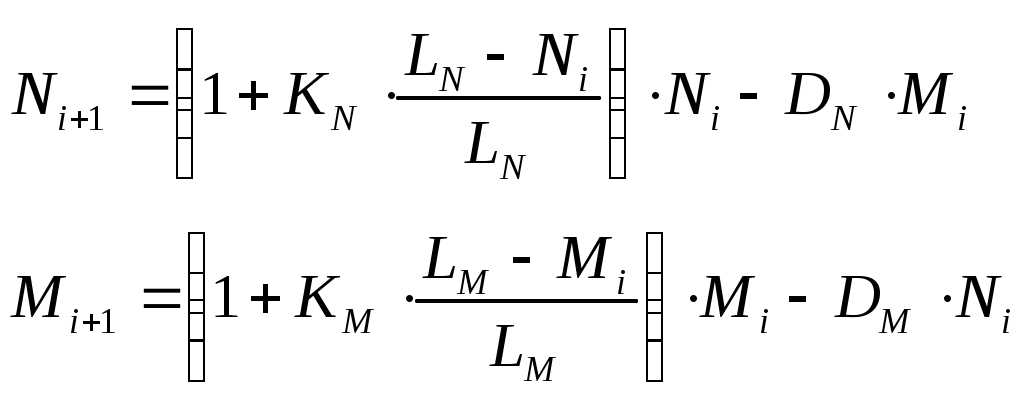
Здесь и – численность белок и бурундуков; и – их максимальные численности; и
– коэффициенты прироста; и – коэффициенты взаимного влияния.

Объясните, на основании каких предположений была построена эта модель.

Ответ:

Выполните моделирование изменения численности двух популяций в течение 15 периодов при , , , , и . Постройте графики изменения численности обеих популяций на одном поле.

Ответьте на следующие вопросы:

  1. Является ли эта модель системной? Почему?

Ответ:

  1. Какова численность белок и бурундуков в состоянии равновесия?

Ответ:

  1. Что влияет на состояние равновесия?

Ответ:

  1. На что влияет начальная численность животных?

Ответ:

  1. При каком значении коэффициента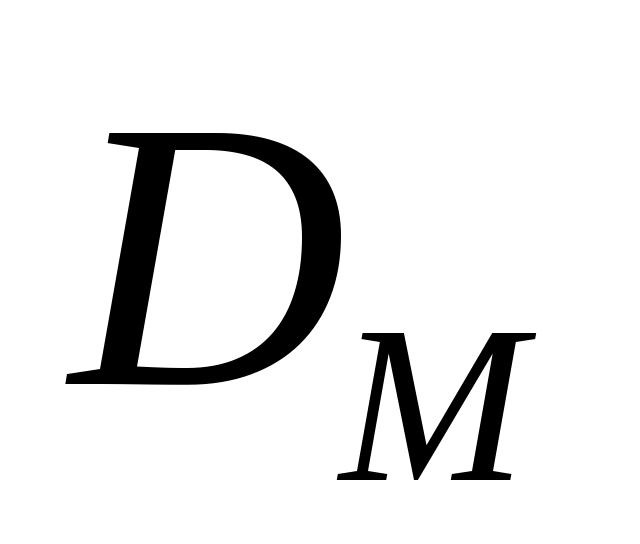 бурундуки вымрут через 25 лет? (используйте подбор параметра).

Ответ:

  1. Найдите какие-нибудь значения коэффициентов, при которых модель становится неадекватна;

Ответ:

  1. Предложите аналогичную модель взаимного влияния трех видов.

Ответ:


      1. Саморегуляция


Для выполнения работы откройте файл-заготовку Саморегуляция.xls.

Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:

, (*)

Эта модель отличатся от модели ограниченного роста только дополнительным множителем , где и – некоторые числа (параметры), смысл которых вам предстоит выяснить.

  1. Выполните моделирование для 30 периодов при следующих значениях параметров модели:



Сравните результаты, которые дают модель классическая модель ограниченного роста и модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.

Ответ:

  1. Постепенно увеличивая коэффициент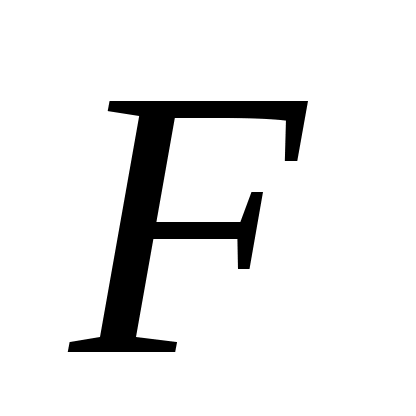 от 0 до 500, выясните с помощью моделирования, как влияет этот коэффициент на саморегуляцию.

Ответ:

  1. Через 10 периодов в результате изменения природных условия число животных уменьшилось до 400 (то есть,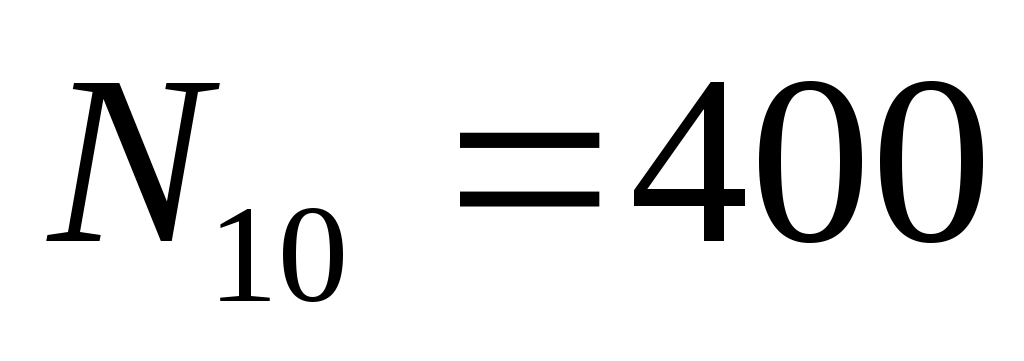 ). Выполните моделирование при этих условиях и опишите, как работает саморегуляция и чем отличается поведение двух сравниваемых моделей.

Ответ:

  1. Повторите моделирование п. 3 при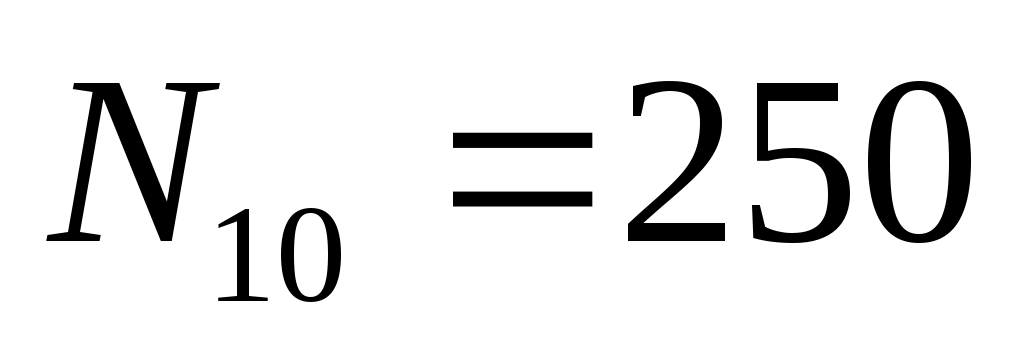 и сделайте аналогичные выводы:

Ответ:

  1. Экспериментируя с моделями, найдите минимальную численность популяции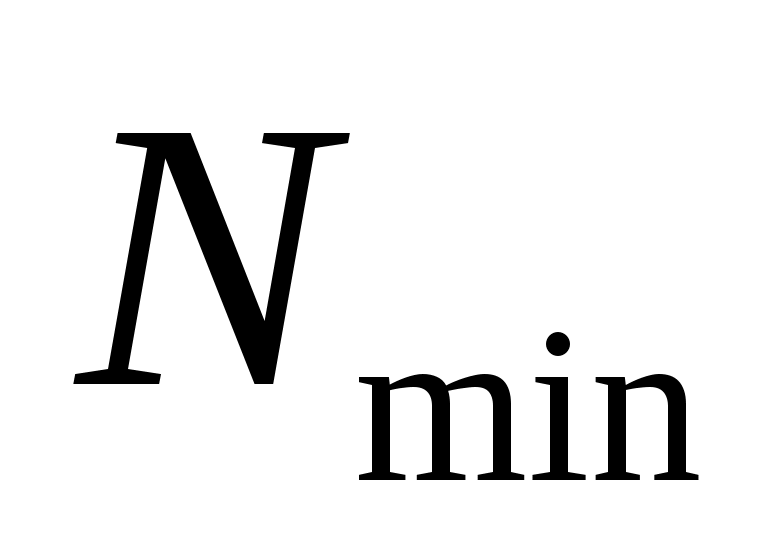 , при которой она выживает в соответствии с моделью (*).

Ответ:

  1. Сделайте выводы о смысле коэффициента в модели (*).

Ответ:

  1. Сравните свойства саморегуляции для модели ограниченного роста и модели (*).

Ответ:


      1. Моделирование работы банка


Для моделирования обслуживания клиентов в банке предложена следующая модель:

  • за 1 минуту в банк входит случайное число клиентов, от 0 до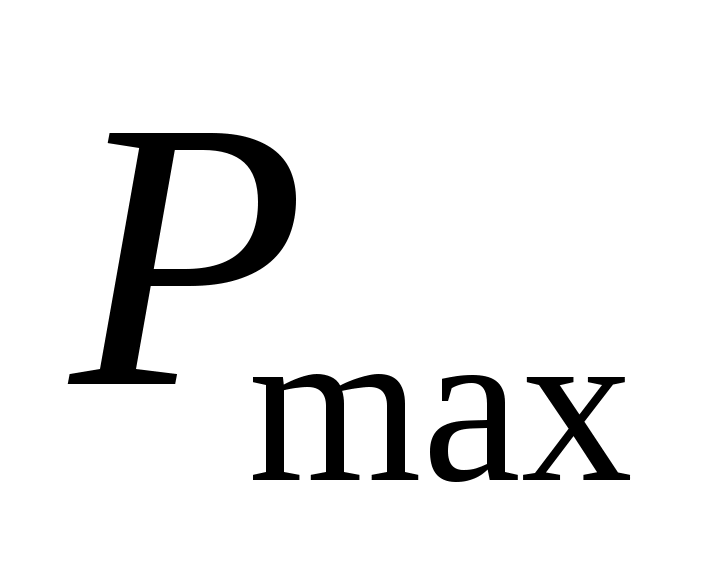 (распределение равномерное);

  • на обслуживание клиентов требуется от до 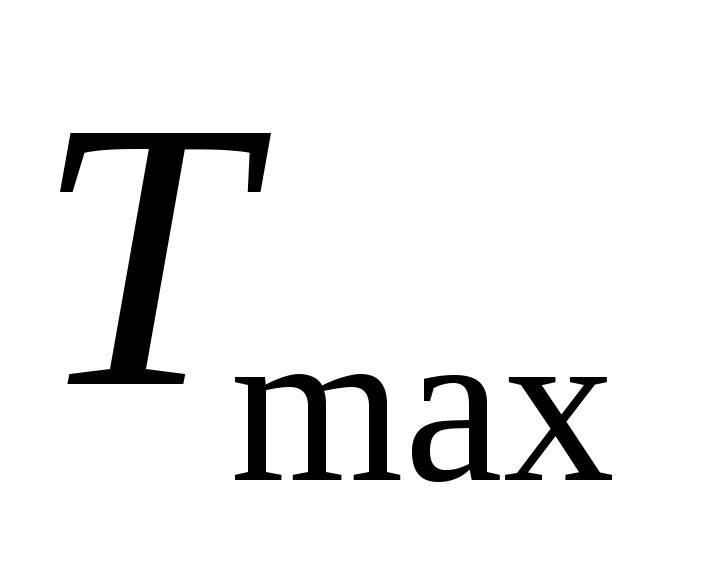минут; время обслуживания 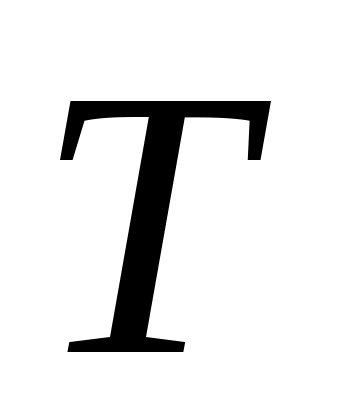определяется для каждой рабочей минуты случайным образом (распределение равномерное);

  • моделирование выполняется для интервала времени , равного 8-часам (рабочая смена).

  • число клиентов, находящихся в помещении банка, вычисляется по формуле



где – количество клиентов, вошедших за -ую минуту, а – количество клиентов, обслуженных за это время;

  • если кассир обслуживает клиента за минут, то можно считать, что за 1 минуту он сделает часть работы, равную 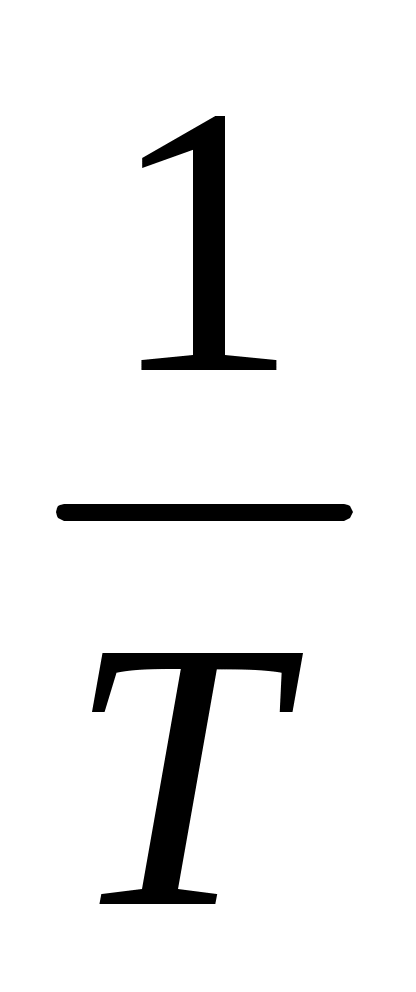; если предположить, что скорость работы кассиров одинакова, то касс за 1 минуту обслужат 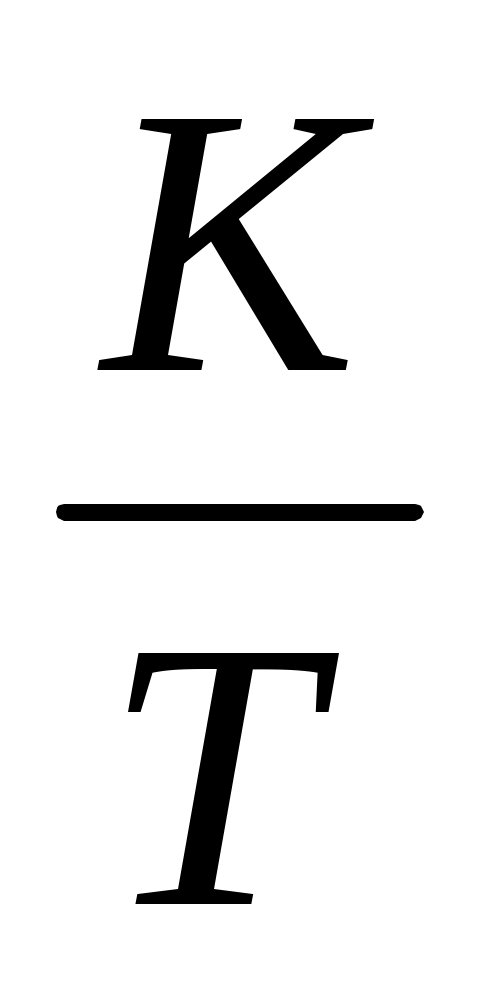клиентов;

  • если считать, что клиентов равномерно распр

Смотрите также файлы