Файл: Линии и поверхности второго порядка.docx

Министерство транспорта Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)

Институт транспортной техники и систем управления

Кафедра «Электропоезда и локомотивы»

Математика

Курсовая работа на тему:

«Линии и поверхности второго порядка»

Выполнил:

ст.гр. ТПЭ-141

Калядин А.А.

Проверил:

доцент

Гиоргадзе М.Г.

Москва 2022

1 Общее уравнение линии второго порядка

Важной задачей аналитической геометрии является исследование общего уравнения линии второго порядка и приведение его к простейшим (каноническим) формам.

Определение: Кривой второго порядка называется множество точек М (х; у) на плоскости ХОУ, координаты которых удовлетворяют следующему общему уравнению кривой второго порядка:

Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0, (1)

где коэффициенты А, 2В, С, 2D, 2E и F – любые числа и, кроме того, числа А, В и С не равны нулю одновременно, т.е. А2 + В2 + С2 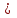0.

2 Эллипс

Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; требуется, чтобы эта постоянная была больше расстояния между фокусами. Фокусы эллипса принято обозначать через F1 и F2.



Рисунок 1 - Эллипс

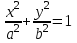- это уравнение называется каноническим уравнением эллипса, где а и b - длины большой и малой полуосей эллипса. При a = b фокусы F1 и F2 совпадают, и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса.

Уравнение 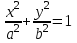, определяющее эллипс в некоторой системе декартовых прямоугольных координат, есть уравнение второй степени; таким образом, эллипс есть линия второго порядка.

---

Оси симметрии эллипса называются его осями, а центр симметрии (точка пересечения осей) – центром эллипса. Точки, в которых эллипс пересекает оси, называются его вершинами. Так как на основании равенства a 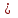b, то 2а ‑ длина большой оси симметрии эллипса, 2b – малой оси. Следовательно, числа а и b являются длинами соответственно большой и малой полуосей эллипса.

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси; обозначив эксцентриситет буквой ε, получаем:

.

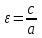Эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше 1— ε2, тем меньше, следовательно, отношение 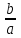; значит, чем больше эксцентриситет, тем более эллипс вытянут вдоль большей оси. В случае окружности b=a и ε=0.

Эксцентриситет эллипса характеризует меру вытянутости эллипса.

Пример 1. Составить каноническое уравнение эллипса, проходящего через точки М1 (2; 3) и М2 (1; ).

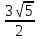Решение: Пусть искомое уравнение эллипса имеет вид . Координаты данных точек удовлетворяют этому уравнению. Подставив вместо х и у сначала координаты точки М1, а затем координаты точки М2, получим систему уравнений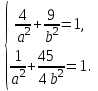



Полагая 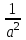= m; 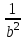= n, приходим к системе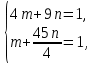



решив которую, найдем m = 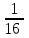, n = 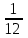, откуда а2 = 16, b2 = 12. Следовательно, искомое уравнение эллипса имеет вид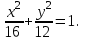
3 Гипербола
Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению; кроме того, требуется, чтобы она была меньше расстояния между фокусами и отлична от нуля. Фокусы гиперболы принято обозначать через F1 и F2, а расстояние между ними — через 2с.

---

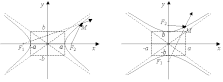
Рисунок 2 - Гипербола

Уравнение 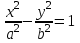, определяющее гиперболу в некоторой системе декартовых прямоугольных координат, есть уравнение второй степени; таким образом, гипербола есть линия второго порядка. Оси симметрии называются осями гиперболы, а центр симметрии (точка пересечения осей) – центром гиперболы. Одна из осей пересекается с гиперболой в двух точках, которые называются ее вершинами. Эта ось называется действительной осью гиперболы. Другая ось не имеет общих точек с гиперболой и называется мнимой осью гиперболы. Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы. Гипербола с равными полуосями (а = b) называется равносторонней, и ее каноническое уравнение имеет вид: х2 – у2 = а2.

Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к расстоянию между ее вершинами; обозначив эксцентриситет буквой ε, получим:

.

Эксцентриситет гиперболы характеризует форму ее основного прямоугольника, а значит, и форму самой гиперболы.

(в направлении оси, соединяющей вершины). Чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник.

Пример 2. Дано уравнение гиперболы 3х2 – 4у2 = 12. Найти ее действительную и мнимую полуоси, координаты фокусов, эксцентриситет; составить уравнения ее асимптот.

Решение: Приведем уравнение гиперболы к каноническому виду:

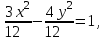или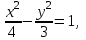

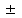
откуда находим, что действительная полуось а = 2, а мнимая полуось b = √3. Так как асимптоты гиперболы имеют уравнения у = 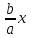, фокусы – координаты (-с; 0) и (с; 0) эксцентриситет , а с = 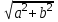= 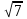, то для данной гиперболы получаем: координаты фокусов (-√7; 0) и (√7; 0);

Эксцентриситет

---

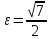
Уравнения асимптот у =

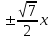
4 Директрисы эллипса и гиперболы

Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии 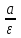от него, называются директрисами эллипса. (а – большая полуось, ε – эксцентриситет эллипса).

Уравнения директрис в выбранной системе координат имеют вид:

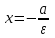и .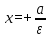

Первую из них мы условимся называть левой, вторую — правой. Так как для эллипса ε<1, то



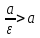
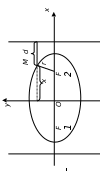
Рисунок 3 – Директриса эллипса

Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и расположенные симметрично относительно центра на расстоянии 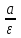от него, называются директрисами гиперболы.

Уравнения директрис в выбранной системе координат имеют вид

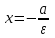и .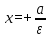

Первую из них мы условимся называть левой, вторую — правой.

Так как для гиперболы ε >1, то



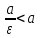
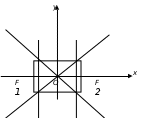
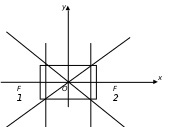
Рисунок 4 – Директриса гиперболы

Теорема 1. Если r – расстояние от произвольной точки М эллипса до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение 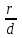величина постоянная, равная эксцентриситету эллипса.

Теорема 2. Если r – расстояние от произвольной точки М гиперболы до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение 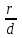величина постоянная, равная эксцентриситету гиперболы.

---

Множество точек, для которых отношение расстояний до фокуса и до соответствующей директрисы величина постоянная, равная ε, это эллипс, если ε < 1, и гипербола, если ε > 1.

5 Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус).

Фокус параболы принято обозначать буквой F, расстояние от фокуса до директрисы — буквой p. Величину р называют параметром параболы.



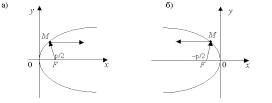
Рисунок 5 - Парабола
у2=2рх – это уравнение называется каноническим уравнением параболы

Уравнение у2=2рх, определяющее параболу в некоторой системе декартовых прямоугольных координат, есть уравнение второй степени; таким образом, парабола есть линия второго порядка.

Точка О называется вершиной параболы, ось симметрии (ось Ох) – осью параболы. Число р, т.е. параметр параболы, как известно, выражает расстояние от фокуса до директрисы.

Парабола, уравнение которой у2 = -2рх, р > 0, расположена слева от оси ординат. Вершина этой параболы совпадает с началом координат, осью симметрии является ось Ох.

Пример 3. Дано уравнение параболы у2 = 6х. Составить уравнение ее директрисы и найти координаты ее фокуса.

Решение. Сравнивая данное уравнение с каноническим уравнением параболы, заключаем, что 2р = 6, откуда р = 3.

Так как фокус параболы имеет координаты ( 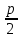; 0), а директриса – уравнение х = 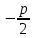, то для данной параболы получаем: координаты фокуса ( 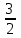; 0) и уравнение директрисы х = .

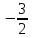6 Поверхности второго порядка

Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.

7 Эллипсоид

---