Файл: Линии и поверхности второго порядка.docx

Рисунок 6 - Эллипсоид

Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:

(1)

Уравнение (1) называется каноническим уравнением эллипсоида.

Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями

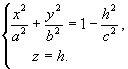 (2)

Исследуем уравнения (2) при различных значениях h.

Если 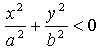 > c (c>0), то   и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует.

Если  , то   и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости   касаются эллипсоида).

Если  , то уравнения (2) можно представить в виде

откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосям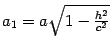и   и   .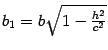

Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность. Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.

8 Однополосный гиперболоид

---

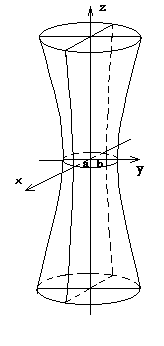
Рисунок 7 – Однополосный гиперболоид

Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

, (a>0, b>0, c>0) (3)

Уравнение (3) называется каноническим уравнением однополосного гиперболоида.

Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения



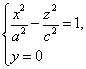
и



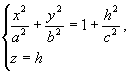
из которых следует, что в сечениях получаются гиперболы.

Аналогично в плоскости x0z имеем гиперболу



В плоскости z=0 имеем эллипс (горловина)



Сечение z=±h, (h>0) даёт нам эллипс



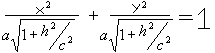
Очевидно, что полуоси этого эллипса возрастают по мере удаления от начала координат.

В сечениях плоскостями, параллельными координатным плоскостям x0z и y0z получим гиперболы.

9 Эллиптический параболоид



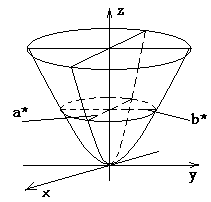
Рисунок 8 – Эллиптический параболоид

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

,(7)

где p>0 и q>0.

Уравнение (7) называется каноническим уравнением эллиптического параболоида.

Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения



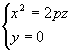
и

---

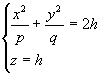
из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.

В сечении плоскостью z=h (h>0) имеем эллипс



Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.

Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.

В случае p=q, то поверхность называется параболоидом вращения.

10 Гиперболический параболоид

Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением

, (p>0, q>0) (9)



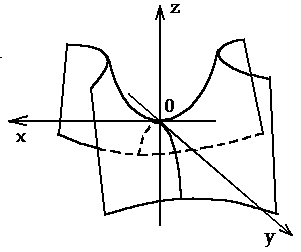
Рисунок 9 – Гиперболический параболоид

Уравнение (9) называется каноническим уравнением гиперболического параболоида.

Рассмотрим сечение параболоида плоскостью xOz (y=0). Получаем уравнение



(10)



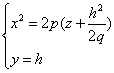
из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h),получаются так же направленные вверх параболы.



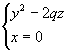
рассмотрим сечение данного параболоида плоскостью Oyz (x=0).

Получаем уравнение



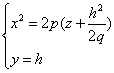
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения

---

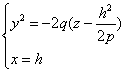
из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).

Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения



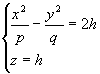
или



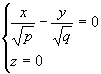
Проводя другие сечения, приходим к выводу, что поверхность имеет форму седла.

11 Конус второго порядка



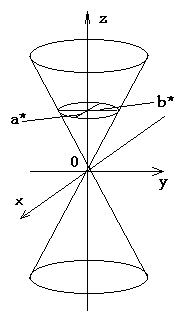
Рисунок 10 – Конус второго порядка

Формула конуса: 

Определение: Канонической поверхностью называется поверхность, которая получается при движении прямой (образующей), проходящей через данную точку (вершину) и пересекающей данную линию (направляющую).

Если направляющей служит кривая второго порядка, то конус называется конусом второго порядка.

Если напраляющая есть замкнутая кривая, то конус представляет собой двуполостную поверхность, все образующие которой проходят через данную точку (вершину конуса). На рисунке 10 изображён конус, имеющий уравнение  . Исследовать форму этого конуса нетрудно, проведя различные сечения этой поверхности.

Отметим еще одну важную особенность уравнения конуса: как правило это однородное уравнение относительно разностей (x-a), (y-b), (z-c), где точка M₀(a,b,c) – вершина конуса. На рисунке 10 изображён конус с вершиной в начале координат, т.е. для данного конуса a=0, b=0, c=0.

---