ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 114
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тогда математическая модель транспортной задачи состоит в определении минимального значения функции
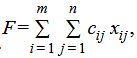 |
-
Что такое условие баланса и какова его роль в транспортных задачах?
Это условие для решения закрытых и открытых транспортных задач (ЗТЗ). ешение задачи с неправильным балансом сводится к решению задачи с правильным балансом введением в ее математическую модель фиктивного поставщика или фиктивного потребителя. Тарифы на перевозку грузов от таких поставщиков или к таким потребителям полагаются равными 0 (т.е. фактически соответствующие перевозки не производятся). Транспортная задача с правильным балансом состоит в том, чтобы найти оптимальный план по заданной таблице перевозок, при котором стоимость перевозок будет минимальна. Такая задача актуальна в областях связанных с транспортировкой грузов.
-
Сформулируйте задачу целочисленного линейного программирования.
Под задачей целочисленного линейного программирования (ЦЛП) понимается задача линейного программирования, в которой некоторые (а возможно, и все) переменные должны принимать целые значения. Задача ЦЛП называется полностью целочисленной, если все её переменные должны быть целочисленными. Задачу ЦЛП можно решить, например, как задачу ЛП без учёта условий целочисленности переменных, а затем округлить полученное решение. Использование такого подхода требует проверки допустимости полученного решения. Таким методом часто пользуются при решении практических задач, особенно когда значения переменных настолько велики, что можно пренебречь ошибками округления. Однако при решении задач, в которых целочисленные переменные принимают малые значения, округление может привести к далёкому от истинного оптимума целочисленному решению. Кроме того, при решении задач большой размерности такой метод требует слишком много машинного времени. Например, пусть оптимальное решение соответствующей задачи ЛП имеет вид x1 = 2,4; x2 = 3,5 . Для получения приближённого оптимального решения необходимо рассмотреть четыре точки (2;3); (2;4); (3;3); (3;4) и выбрать среди них допустимую точку с наилучшими значениями целевой функции. Если в задаче имеются 10 целочисленных переменных, то следует рассмотреть 210 = 1024 варианта целочисленного решения. Но даже рассмотрение всех вариантов не гарантирует получения оптимального целочисленного решения задачи.
Одним из методов решения как полностью целочисленных, так и смешанных задач ЦЛП является метод ветвей и границ. Он представляет собой эффективную процедуру перебора всех целочисленных допустимых решений.
-
Сформулируйте задачу о рюкзаке. К какому классу задач целочисленного программирования она относится?
Задача о рюкзаке (также задача о ранце) — NP-полная задача комбинаторной оптимизации. Своё название получила от конечной цели: уложить как можно большее число ценных вещей в рюкзак при условии, что вместимость рюкзака ограничена.
В общем виде задачу можно сформулировать так: из заданного множества предметов со свойствами «стоимость» и «вес» требуется отобрать подмножество с максимальной полной стоимостью, соблюдая при этом ограничение на суммарный вес.
Задача о рюкзаке. 1. Классы задач. Класс P — класс задач с полиномиальной сложностью или класс полиномиально-решаемых задач. ... Задачи класса P. Задача называется полиномиальной, т. е. относится к классу P, если существует константа k и алгоритм, решающий эту задачу за время O(nk), где n есть длина входа алгоритма в битах. Это задачи, решаемые за реальное время. Преимущества ... Динамическое программирование обычно применяется к задачам, в которых искомый ответ состоит из частей, каждая из которых в свою очередь дает оптимальное решение некоторой подзадачи.
-
Сформулируйте задачу о коммивояжере. К какому классу задач целочисленного программирования она относится?
Сформулированная задача - задача целочисленная. Пусть хij = 1 , если путешественник переезжает из i -ого города в j-ый и хij = 0, если это не так. Формально введем (n+1) город, расположенный там же, где и первый город, т.е. расстояния от (n+1) города до любого другого, отличного от первого, равны расстояниям от первого города. ... Условия задачи: Необходимо посетить 4 города в ходе деловой поездки Спланировать поездку нужно так, чтобы, переезжая из города в город, побывать в каждом не более одного раза и вернуться в исходный город. Определить оптимальный маршрут посещения городов и его минимальное расстояние.
Задача коммивояжёра относится к числу трансвычислительных: уже при относительно небольшом числе городов (66 и более) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет. Содержание. 1 История. ... Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Также задача о коммивояжере может быть сведена к задаче целочисленного линейного программирования путем введения в модель дополнительных ограничений.
-
В чем состоит суть задачи раскроя?
Задача раскроя — это NP-полная задача оптимизации, по существу, сводимая к задаче о ранце. Задача является задачей целочисленного линейного программирования. Задача возникает во многих областях промышленности. Представим себе, что вы работаете на целлюлозно-бумажном предприятии, и у вас имеется некоторое количество рулонов бумаги фиксированной ширины, но различным заказчикам нужны различные количества рулонов различной ширины. Как разрезать бумагу, чтобы минимизировать отходы?
-
Для каких оптимизационных задач применяется метод динамического программироваия?
Динамическое программирование это способ решения сложных задач путём разбиения их на более простые подзадачи. Часто его применяют к целочисленным задачам оптимизации, сводя их к последовательности целочисленных оптимизационных задач меньшей сложности.
При его реализации одновременный выбор значений большого числа переменных решаемой экстремальной задачи заменяется поочередным опре-делением каждой из них в зависимости от возможных обстоя-тельств.
Динамическое программирование придерживается двух подходов к решению задач:
-
Нисходящее динамическое программирование, когда исходная задача разбивается на подзадачи. После решения подзадач результаты объединяются для получения решения исходной задачи. -
Восходящее динамическое программирование, когда сначала происходит решение подзадач, а затем объединение их результатов для решения общей задачи.
-
В чем заключается суть метода динамического программирования?
Динамическое программирование – это метод, который позволяет эффективно решать многие задачи, прежде всего, задачи комбинаторной оптимизации. Суть метода в следующем: имеющуюся задачу рекурсивно разбиваем на более маленькие подзадачи, их — на ещё меньшие и так далее.
-
Сформулируйте принцип оптимальности Беллмана.
Принцип оптимальности впервые был сформулирован Ричардом Эрнестом Беллманом в 1953 г. (в трактовке Е.С. Вентцель): Каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление таким образом, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Принцип оптимальности Р. Беллмана сформулирован для решения широкого круга задач управления, планирования производственной деятельности, распределения различного рода ресурсов, конструирования, проектирования и др. и вообще для задач принятия решений в многошаговых (многоэтапных) процессах.
Если заданы начальное (точка А) и конечное (точка В) состояния некоторой системы, и переход из начального в конечное состояние осуществляется в несколько промежуточных этапов, на каждом из которых система может находиться в одном из нескольких состояний, и каждому переходу на каждом этапе можно сопоставить некоторые затраты (или прибыль), то задача состоит в том, чтобы выбрать такой путь (то есть все промежуточные состояния), для которого суммарные затраты достигают минимума (или прибыль -максимума). Предположим, что количественная оценка пути это суммарные затраты (сумма затрат по этапам, т.е. сумма шаговых затрат). Пусть на первом этапе из начального состояния (точка А) можно перейти в некоторое конечное число состояний (условно это четыре точки на вертикали 1 рис. 3.5) с соответствующими затратами. Далее, аналогично, из состояний первого этапа (результатов первого шага) можно перейти в конечное число состояний (три точки на вертикали 2) и т.д., вплоть до конечного этапа, на котором из всех возможных состояний возможен переход только в одно конечное состояние (точка В).
-
Дайте понятие идентификации в широком и узком смысле.
Задачи идентификации в узком смысле
В зависимости от характера априорной информации об объекте различают задачи идентификации в узком и широком смысле. Задача идентификации в узком смысле сводится к оценке параметров объекта по результатам наблюдений за входными и выходными сигналами, полученными в условиях функционирования объекта. Априорная информация об объекте при этом должна быть достаточно велика, внутренняя структура объекта известна и задан класс моделей, к которому можно отнести данный объект
Задача идентификации в широком смысле ставится в случае, когда априорная информация об объекте недостаточна, в связи с чем возникает необходимость выбора структуры системы (объекта) и задания класса моделей, оценки степени и формы влияния входных переменных на выходные и т. д.
Идентификация в широком смысле является пока не столько наукой, сколько искусством, так как определение адекватной структуры модели при большом многообразии конкретных объектов требует определенной интуиции исследователя, знания конкретных особенностей и основных физических закономерностей функционирования объекта. Построение хорошей модели – это, как правило, многоэтапный процесс, заключающийся в последовательной постановке и проверке гипотез о структуре и параметрах объекта.
-
Опишите структурную схему процесса идентификации.
Первая проблема (структурная идентификация) является, по существу, основной проблемой всего процесса моделирования, состоящего из рассмотренных в гл. I следующих четырех основных этапов:
постановка задачи
выбор структуры модели и математическое описание ее блоков;
исследование модели;
экспериментальная проверка модели.
По крайней мере, с этой проблемой смыкаются три первых этапа моделирования. Ей посвящены гл. 1-4, в которых рассматривались возможности использования фундаментальных закономерностей для вскрытия внутреннего механизма и взаимосвязей в объекте, а также формирования адекватной структуры модели. Полная формализация этой проблемы вряд ли возможна из-за большого многообразия и практически неисчерпаемой сложности реальных объектов. Здесь велика роль профессионализма исследователя, знание физического механизма процессов, правильной формулировки цели и постановки задачи.