Объектами идентификации являются продукция, услуги, ценные бумаги (деньги, акции, векселя и др.), информация, рабочая сила и другие объекты коммерческой деятельности. В данном учебном пособии разберем лишь одну группу объектов — продукцию, которая вовлекается в процесс купли-продажи и становится товаром. Именно об идентификации продовольственных товаров в сфере торговли и у потребителя, приобретающего товары, пойдет речь, хотя следует отметить, многие рассматриваемые вопросы в равной степени могут быть отнесены и к непродовольственным товарам.

31. 
    Какова цель параметрической идентификации?
    

Параметрическая идентификация — определяются значения параметров модели. Методы идентификации: Активные (можно подавать на вход объекта тестовые сигналы) и пассивные. Детерменированые и статистические (учитывают наличие шума). Оперативные (идентификация проходит “налету”) и ретроспективные. Целью данного этапа является построение адекватной модели системы в общем контексте решения исходной проблемы. Задача параметрической идентификации сводится к отысканию таких оценок параметров модели, которые обеспечивают наибольшую, в каком либо смысле близость значений на выходе, рассчитанных по модели и, полученных в эксперименте, при одинаковом значении входных данных.

32. 
    Что такое функция локальной невязки?
    

Невязка — величина ошибки (расхождения) приближённого равенства.

Если точное решение неизвестно, можно использовать аппроксимацию решения с небольшой невязкой.Невязка фигурирует во многих разделах математики, в том числе в итерационных методах, таких как метод обобщенного минимума, в котором решение системы уравнений находится путём минимизации невязки.В навигации невязкой называется расстояние между вычисленным по прокладке местоположением судна и фактически определённым (по светилам, маякам и т.д.) местоположением, измеряется в морских милях

33. 
    Какие критерии могут быть использованы в качестве суммарной невязки?
    

Невязка — величина ошибки (расхождения) приближённого равенства. Пусть требуется найти такое x, что значение функции: Если точное значение x неизвестно, вычисление ошибки невозможно, однако при этом может быть определена невязка

---

. Суммарная невязка представляет собой сумму этих функций и является результатом их интерференции. Функцию распределения суммарной невязки можно получить следующим образом. Вначале получим плотность вероятности квадрата одной случайной величины, а затем по закону сложения случайных величин можно получить искомую плотность вероятности. Для вычисления функции распределения квадрата суммарной невязки воспользуемся характеристическими функциями

34. 
    При каком значении относительной невязки модель считается адекватной?
    

Если относительная невязка меньше предельно допустимой, то производят увязку приращения, заключающуюся в изменении величины каждого приращений с таким расчетом, чтобы алгебраическая сумма всех приращений получилась равной нулю. Для этого 2 Дх и 2Ду распределяют с обратным знаком между приращениями пропорционально длине сторон.  [4]

Если относительная невязка допустима, то вычисленные приращения увязывают, вводя в них поправки. 

1. 
   Сформулируйте общую задачу линейного программирования
   

Линейное программирование (ЛП) – это раздел математики, в котором изучаются методы решения задач на отыскание экстремумов линейных функций многих переменных при наличии линейных ограничений, наложенных на переменные.

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции



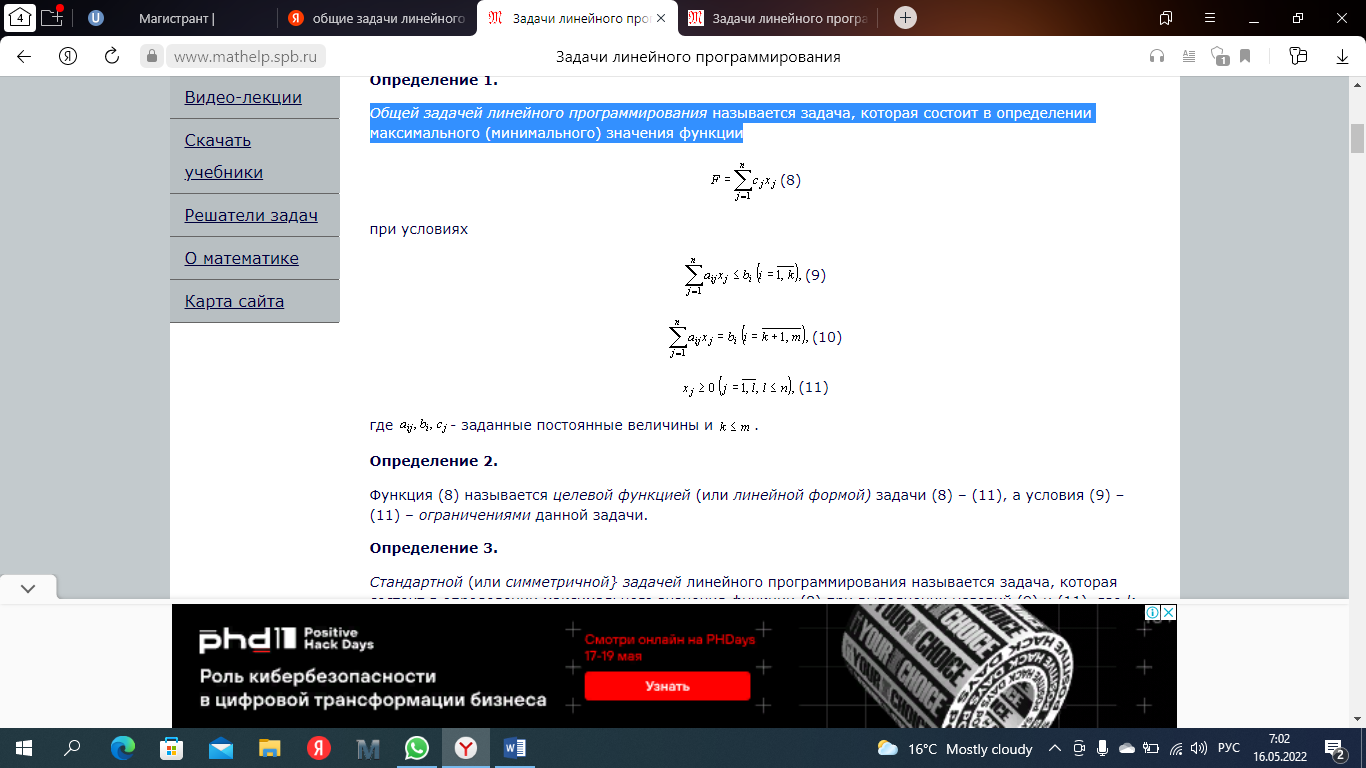
Определение 2.Функция (8) называется целевой функцией (или линейной формой) задачи (8) – (11), а условия (9) – (11) – ограничениями данной задачи.

Определение 3.Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.

Определение 4.Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п.

Определение 5.Совокупность чисел  ,удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).

Определение 6.План 

---

, при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.

Значение целевой функции (8) при плане Х будем обозначать через  . Следовательно, X^* – оптимальный план задачи, если для любого Х выполняется неравенство  [соответственно  ].

2. 
   Чем отличается основная задача линейного программирования от общей?
   

общая задача линейного программирования – это задача, в которой требуется найти максимум или минимум (оптимум) функции, называемой функцией цели, при ограничениях, заданных системой линейных неравенств или уравнений.

Основная задача линейного программирования отличается от задачи программирования общего вида тем, что ограничения в ней заданы в виде системы уравнений: Из курса линейной алгебры известно, что такая система либо не имеет решений, либо имеет единственное решение или бесчисленное множество решений. Будем полагать, что оптимальное решение единственно, хотя на практике их может быть несколько. Если система не имеет решений, ее анализируют повторно, в соответствии с имеющейся конкретной практической ситуацией. Те уравнения, которые являются причиной отсутствия решений, исключаются из системы.

3. 
   Чем отличается общая задача линейного программирования от канонической?
   

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные xj налагаются условия неотрицательности, то она называется задачей линейного программирования в канонической форме или канонической задачей линейного программирования (КЗЛП).

Общая задача линейного программирования – это задача, в которой требуется найти максимум или минимум (оптимум) функции, называемой функцией цели, при ограничениях, заданных системой линейных неравенств или уравнений.

Отличие КП от ОЗ в канонической форме записи задач линейного программирования все переменные, входящие в систему ограничений, должны быть неотрицательными.

---

4. 
   Какие ограничения называют жесткими (нежесткими)?
   

Жесткость и нежесткость ограничений ЛП [hardness and slackness of LP constraints] — характеристика ограничений задачи линейного программирования по степени их влияния на оптимум (см. Чувствительность оптимального решения). Ограничение является нежестким, когда малые изменения константы ограничения не отражаются на решении задачи. Например, в распределительной задаче это означает, что спрос строго меньше предложения, в результате чего объективно обусловленные оценки равны нулю. Решение не зависит от общего объема возможного предложения товара, так как имеющееся количество его превышает ту потребность в нем, которая соответствует его использованию в оптимальной точке.

Ограничение является жестким, когда любое малое изменение константы (параметра) ограничения приводит к изменению значения целевой функции (то есть объективно обусловленная оценка не равна нулю).

5. 
   Приведите примеры существенных и несущественных ограничений.
   

Существенные и несущественные свойства математических объектов раскрываются в процессе определения понятий математики. Множество существенных свойств составляют содержание понятия.

Под существенными свойствами будем понимать те, без которых понятие не существует, и при помощи которых выделяются объекты интересующего нас множества. Существенные свойства – это всегда общие свойства, но обратное неверно – общие свойства могут быть несущественными. Так, в школьных учебниках в уравнениях преобладает обозначение переменной – “х”. Это свойство общее, но не существенное.
Кроме того, понятия “существенное” и “несущественное” свойство относительны, в разных ситуациях одно и то же свойство математического объекта может быть как существенным, так и несущественным. Например, при выделении линейных функций среди других знак коэффициента при х – несущественное свойство, но оно же становится существенным при выделении среди линейных функций возрастающих.

6. 
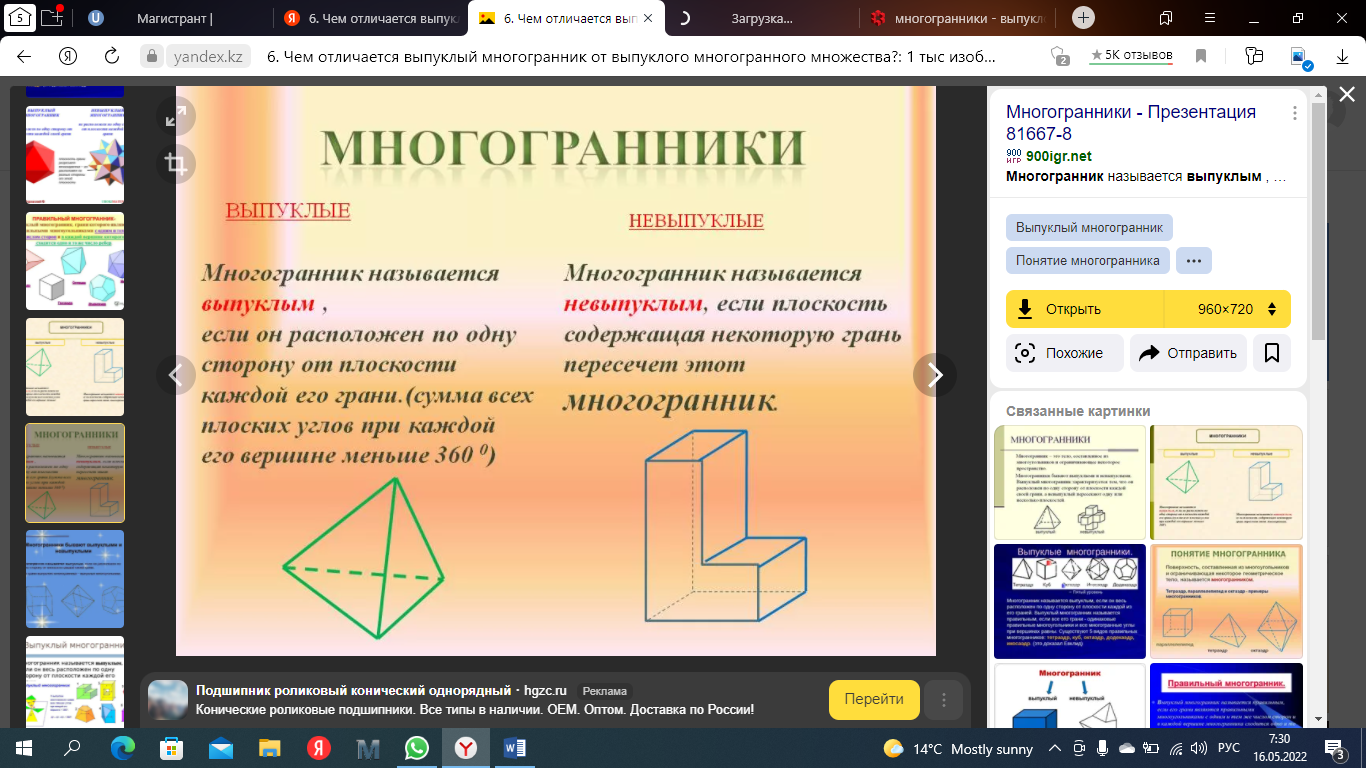
   Чем отличается выпуклый многогранник от выпуклого многогранного множества?
   

Выпуклый многогранник разрезает пространство на две части – внешнюю и внутреннюю. Внутренняя его часть есть выпуклое тело. Обратно, если поверхность выпуклого тела многогранна, то соответствующий многогранник –выпуклый. Теорема. Сумма всех плоских углов выпуклого многогранного угла меньше 360 градусов.

---

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

Общим определяющим свойством, которое отличает выпуклый многоугольник от невыпуклого, является то, что если взять любые две его точки и соединить их отрезком, то весь отрезок будет принадлежать этому многоугольнику. Это свойство может быть принято за определение выпуклого множества точек.

7. 
   Дайте определение угловой точки выпуклого многогранного множества.
   

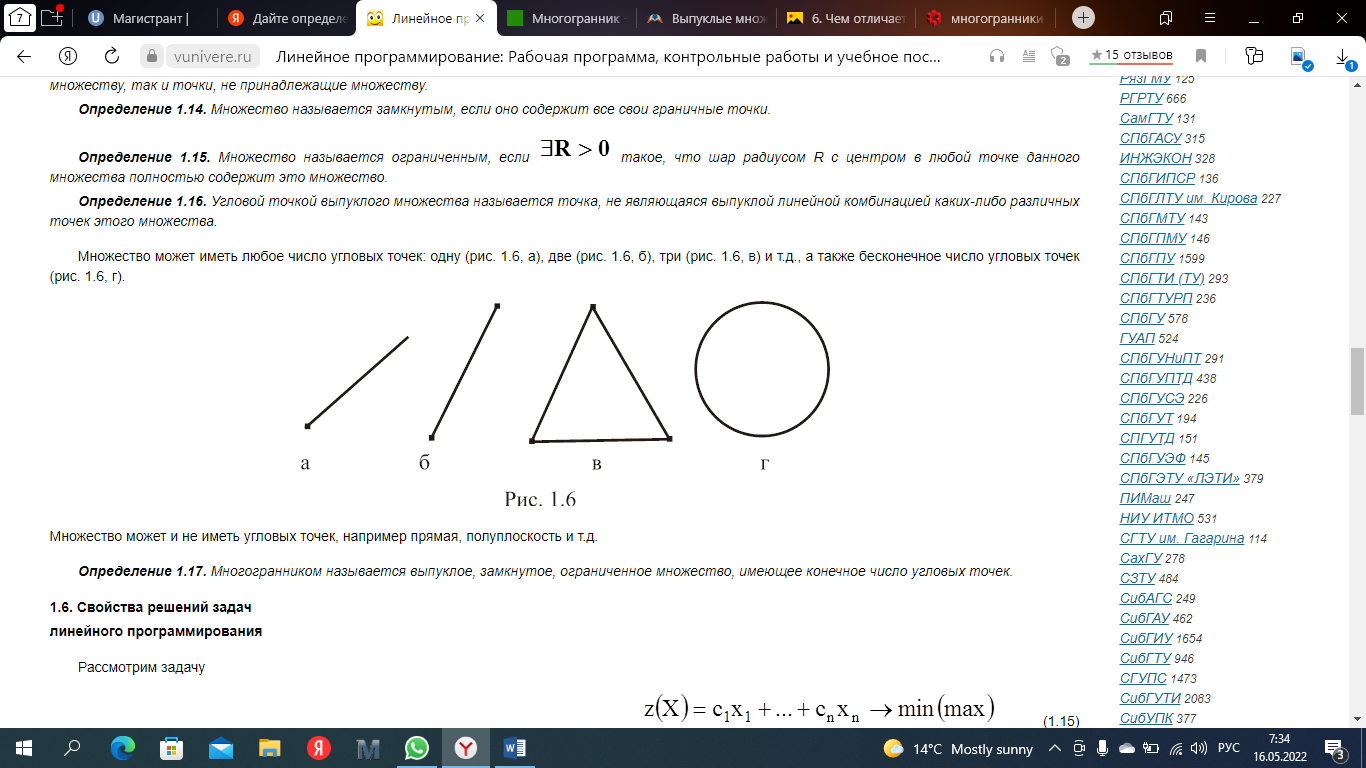
Вектор X, принадлежащий выпуклому множеству V, называют крайней или угловой точкой или вершиной V, если для любых векторов X(1) и X(2) из V при 0≤λ≤1 из того, что X = (1 - λ)X(2) + λX(1), следует, что X = X(1) = X(2). Иначе, X - крайняя (угловая) точка множества V, если X нельзя представить в виде выпуклой комбинации каких-либо двух других точек из V, от нее отличных.
Геометрически это означает, что крайняя точка не может лежать внутри какого-либо отрезка, принадлежащего множеству V.

8. 
   Сформулируйте основную теорему линейного программирования.
   

(основная теорема линейного программирования):

1) Линейная форма достигает своего минимума в угловой точке многогранника решений.

2) Если она принимает минимальное решение более чем в одной угловой точке, то она достигает того же самого значения в любой точке, являющейся выпуклой комбинацией этих угловых точек.

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.
Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , где n - число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.

---

Смотрите также файлы

• Методические указания по оформлению курсовой работы по дисциплинам Гражданское право.pdf

• Технологии.pdf

• Общая характеристика криминалистической идентификации 5 Глава Идентификация огнестрельного оружия 16.rtf

• Анализ технических средств перехвата информации в оптическом диапазоне.docx

• азастан республикасы ылым жне жоары білім министрлігі.docx