Файл: В чем состоит свойство унимодальности функций.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 116

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что , где , то точка является угловой точкой многогранника решений.
Теорема 4: Если - угловая точка многогранника решений, то векторы в разложении , соответствующие положительным, являются линейно независимыми.
Следствие 1: Так как векторы имеют размерность m, то угловая точка многогранника решений имеет не более m положительных компонент .
Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов .

Эта теорема имеет важнейшее значение, так как она указывает путь решения задачи линейного программирования. Совсем не надо перебирать все точки допустимой области. Достаточно перебрать вершины допустимой области, а ведь их - конечное число. Кроме того, как это окажется далее, не нужно перебирать все вершины, можно этот перебор существенно сократить. 

  1. В чем заключается первая геометрическая интерпретация задачи линейного программирования?

Определение 1. Значения неизвестных переменных, удовлетворяющие всем ограничениям задачи линейного программирования, называются допустимыми значениями переменных или планами.

Определение 2. Множество всех планов задачи линейного программирования называется областью допустимых значений переменных (ОДЗ).

Определение 3. План задачи линейного программирования, при котором целевая функция принимает минимальное (или максимальное) значение на ОДЗ называется оптимальным.
Графическим методом в основном решаются задачи с малым числом переменных. Он включает следующие этапы:

1) Находятся геометрические решения всех ограничений задачи.

2) Областью допустимых значений будет многоугольник, полученный с помощью пересечения всех полуплоскостей.

Таким образом, геометрически решить задачу линейного программирования означает найти среди всех точек ОДЗ такую точку (точки), при которой (которых) целевая функция принимает своё экстремальное значение.

Замечание. При нахождении решения задачи линейного программирования графическим методом могут встретиться случаи, изображенные на следующих рисунках.



 

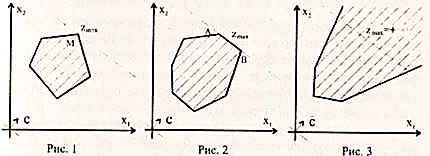
На первом рисунке изображен случай, когда целевая функция принимает максимальное значение в единственной точке М. Из второго рисунка видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ. На третьем рисунке изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений.


Отметим, что нахождение минимального значения целевой функции отличается от нахождения её максимального значения лишь тем, что линия уровня 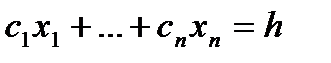  перемещается не в направлении вектора с, а в противоположном направлении.

Графический метод является наглядным и простым методом решения задач линейного программирования. Однако область его применения ограничена размерностью задачи. Если задача представлена в стандартной форме, то количество переменных должно быть не более трёх.



  1. В чем состоит идея геометрического метода решения задачи линейного программирования? Для каких задач он применим?

Геометрический метод решения ЗЛП применяется в случае, если задача содержит не более двух переменных или может быть сведена к таковой. Каждое из неравенств системы ограничений геометрически определяет полуплоскость допустимых значений переменных с граничными прямыми. Алгоритм геометрического метода: 1. В системе ограничений знаки неравенств заменяются на знаки точных равенств и по полученным уравнениям строятся прямые на плоскости x 1 Ox 2.

Геометрические методы обычно применяются для решения двумерных задач линейного программирования, и они основаны на двух важных геометрических свойствах этих задач:

1) областью допустимых решений задачи является выпуклый многоугольник;

2) целевая функция возрастает при движении по направлению ее вектора-градиента.

11. В чем заключается вторая геометрическая интерпретация задачи линейного программирования?

Векторная форма записи КЗЛП и ее применение. Рассмотрим каноническую задачу линейного программирования 



Обозначим через аj столбцы матрицы А и будем рассматривать их как векторы пространства Rm. Тогда каждому допустимому плану КЗЛП — n-мерному вектору х — соответствует неотрицательная линейная комбинация столбцов аj, равная столбцу bÎ Rm:

Такое представление ограничений КЗЛП обычно называют векторной формой записи.

Векторы аj, j Î l:n будем называть векторами требований задачи (D, f), а вектор b — вектором ограничений. Множество всех неотрицательных линейных комбинаций столбцов аj  с геометрической точки зрения может быть представлено как многогранный выпуклый конус, натянутый на систему векторов аj  в пространстве Rm (рис. 1.3).


Соответственно, вопрос о существовании допустимого плана задачи (D, f) равнозначен вопросу о принадлежности вектора b данному конусу, а компоненты хj некоторого допустимого плана х Î D являются не чем иным, как коэффициентами разложения вектора ограничений задачи b по векторам, требований аj.

Такоепредставление КЗЛП получило название второй геометрической интерпретации.

  1. Дайте определения следующих понятий: опорная точка (опорный план) допустимого множества, базис опорной точки, базисные переменные.

Опорным планом (решением) задачи линейного программирования называется допустимый план, для которого векторы условий, соответствующие его положительным координатам, линейно независимы.

Базис - мерного пространства - совокупность любых линейно-независимых векторов .

Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.

Базисные переменные– это переменные задачи ЛП в канонической форме, которые в рассматриваемом опорном плане, не являются свободными. Они имеют неотрицательные значения, которые определяются из решения системы уравнений (

  1. Дайте определение двойственной задачи линейного программирования.

Под двойственной задачей понимается вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Заинтересованность в определении оптимального решения прямой задачи путём решения двойственной к ней задачи обусловлена тем, что вычисления при решении ДЗ могут оказаться менее сложными. Трудоёмкость вычислений при решении ЗЛП в большей степени зависит от числа ограничений, а не от количества переменных.

Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения прямой задачи и соотношения двойственной задачи являются неравенствами вида « «. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.

Двойственная задача тесно связана задачей линейного программирования. Задача первоначальная называется исходной. Решение двойственной задачи может быть получено из решения исходной и наоборот. Связующим фактом этих двух задач являются коэффициенты Cj функции исходной задачи. Данные коэффициенты называются свободными членами системы ограничений двойственной задачи. Коэффициенты Bi системы ограничений исходной задачи называются коэффициентами двойственной задачи. Транспонированная матрица коэффициентов системы ограничений исходной задачи является матрицей коэффициентов системы ограничений двойственной задачи.


  1. Каким свойством обладает отношение двойственности?

теорема двойственности. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива. ... Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенство общей оценки продукции и ресурсов обусловливает убыточность всякого другого плана, отличного от оптимального.

  1. Перечислите основные свойства пары двойственных задач (теоремы двойственности).

Двойственность является фундаментальным понятием в теории линейного программирования. Основные результаты теории двойственности заключены в двух теоремах, называемых теоремами двойственности.

ПЕРВАЯ ТЕОРЕМА ДВОЙСТВЕННОСТИ.

Если одна из пары двойственных задач I и II разрешима, то разрешима и другая, причем значения целевых функций на оптимальных планах совпадают, F(x*) = G(y*), где х*, у* - оптимальные решения задач I и II

ВТОРАЯ ТЕОРЕМА ДВОЙСТВЕННОСТИ.

Планы х* и у* оптимальны в задачах I и II тогда и только тогда, когда при подстановке их в систему ограничений задач I и II соответственно хотя бы одно из любой пары сопряженных неравенств обращается в равенство.
Это основная теорема двойственности. Другими словами, если х* и у* - допустимые решения прямой и двойственной задач и если cTx*=bTy*, то х* и у* – оптимальные решения пары двойственных задач.

ТРЕТЬЯ ТЕОРЕМА ДВОЙСТВЕННОСТИ. Значения переменных yi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений - неравенств прямой задачи на величину целевой функции этой задачи:
Δf(x) = biyi

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи yi, в оптимальном плане называют объективно обусловленными, или двойственными оценками. В прикладных задачах двойственные оценки yi часто называются скрытыми, теневыми ценами или маргинальными оценками ресурсов.



  1. Каково практическое значение теорем двойственности?

Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения основной задачи на решение двойственной, которое в определенных случаях может оказаться более простым. Например, задача, область допустимых значений которой описывается двумя уравнениями, связывающими шесть переменных (m = 2, n = 6), не может быть решена графическим методом. Однако данный метод может быть применен для решения двойственной к ней задачи, которая имеет только две переменные.

Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения основной задачи на решение двойственной, которое в определенных случаях может оказаться более простым.

  1. Какая из теорем двойственности является критерием оптимальности для задач линейного программирования и в чем ее суть?

Первая теорема двойственности. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

  1. Дайте содержательную формулировку и математическую постановку транспортной задачи?

Транспортная задача, это специальный вид задачи линейного программирования. Для решения транспортной задачи можно использовать методы решения задач линейного программирования, однако ввиду специфического вида задачи, были построены алгоритмы специально для решения этой задачи. Для решения транспортной задачи в онлайн режиме с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.

Общая постановка транспортной задачи заключается в определении оптимального плана перевозок некоторого однородного груза из пунктов отправления A1, A2,..., Am в пункты назначения B1, B2,..., Bn. Критерий оптимальности берется минимальная стоимость перевозки или минимальное время доставки груза.

Рассмотрим транспортную задачу, где в качестве критерия оптимальности взята минимальная стоимость перевозок всего груза. Обозначим через Сij тарифы перевозки единицы груза из пункта отправления i в пункт назначения j. Обозначим через Ai запасы груза i-м пункте отправления, а через Bj потребности груза j-м пункте назначения, а через Xj количество единиц груза переводимого из пункта отправления i в пункт назначения j.

Смотрите также файлы