ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 126
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
+
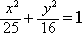44. Укажите уравнение окружности радиуса R= 8 с центром в точке C(2;-5)
-
(x- 2)2+ (y+ 5)2= 82 +
45. Укажите канонические уравнения прямой
-
+
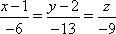46. Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b= 3
-
+
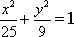47. Укажите канонические уравнения прямой, проходящей через точки M1(3; 2; 5) и M2(-1; 3; -2)
-
+
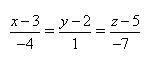48. Найдите ранг и базисные строки матрицы
-
2. 1-я строка, 2-я строка +
49. Найдите ранг матрицы
-
2 -
3 -
4 + -
1
50. Расширенная матрица системы
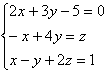имеет вид
-
+
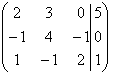51. Вычислить произведение матриц
-
+
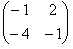52. Матрица называется невырожденной, если
-
Ее определитель не равен нулю +
53. Определитель системы трех линейных неоднородных уравнений с тремя неизвестными равен 5. Это означает, что
-
система имеет единственное решений +
54. Найдите острый угол между прямыми
и 
-
60° +
55. Расширенная матрица системы
имеет вид-
+
56. Укажите уравнение окружности радиуса R= 8 с центром в точке C(2;-5)
-
(x- 2)2+ (y+ 5)2= 82 +
57. Даны точки M(-5; 7; -6), N (7; -9; 9). Вычислите проекцию вектора
на вектор 
-
3 +
58. Укажите канонические уравнения прямой
-
+
59. Какие векторы называются коллинеарными?
-
лежащие на одной прямой или на параллельных прямых +
60. Найдите координаты точки K пересечения прямой
с плоскостью 2x+ 5y- 3z= 0-
+
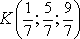61. Вычислить произведение матриц
-
+
62. Найдите общее решение системы
-
+
63. Найдите А В, где
; 
-
+
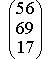64. Найдите угол между векторами a = 2m + 4n и b = m -
n, где m и n - единичные векторы и угол между m и n равен 120°
-
120 +
65. Упростите выражение
-
+
66. Определите полуоси гиперболы 25x2 - 16y2 = 1
-
+
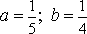67. Чему равен определитель матрицы системы?
-
-7 -
-2 -
-3 -
22 +
68. Матрица
является обратной матрицей к матрице 
, если-
+
69. Решите систему уравнений методом Крамера
-
{(1; 0; 1)} -
{(-1; 0; 1)} + -
{(-1; 0; -1)} -
{(1; 0; -1)}
70. Вычислите определитель
-
102 -
-53 -
-89 + -
89
71. Метод Гаусса решения системы линейных уравнений предполагает использование
-
последовательного исключения неизвестных +
72. Найдите АВ АС, где
; 
; 
-
+
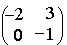73. Система линейных уравнений называется совместной, если
-
она имеет хотя бы одно решение +
74. Определитель матрицы системы
равен-
-7 -
-2 -
-3 -
22 +
75. Матричное уравнение A * X = B имеет решение
-
+
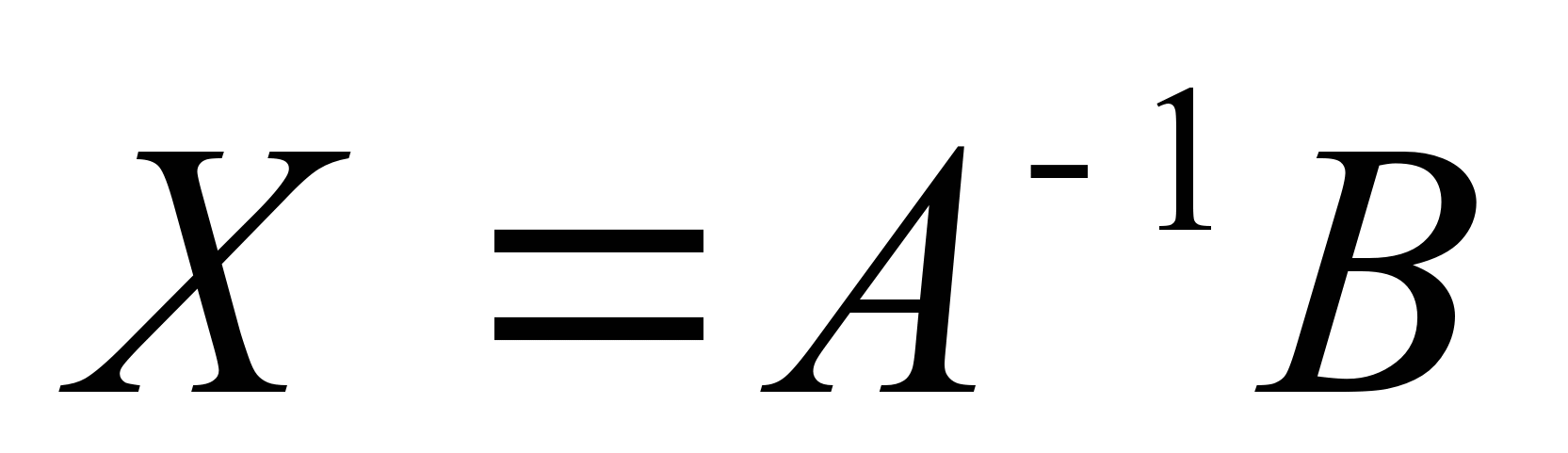76. Найдите А В, где
; 
-
+
77. Найдите обратную матрицу для матрицы
-
+
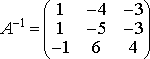78. Решите матричное уравнение AX + AXA = B, где
; 
.-
+
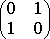79. Раскрыть определитель
-
(a – b)(a + b) +
80. Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x-4y+20=0 является касательной к окружности
-
x2 y2 = 16 +
81. При каком положительном значении параметра t прямые, заданные уравнениями 3tx-8y+1=0 и (1+t)x-2ty=0, параллельны?
-
2 +
82. Даны вершины треугольника ABC:
A(3; -1),B(4; 2) и C(-2; 0). Напишите уравнения его сторон
-
3x - y - 10 = 0, x - 3y + 2 = 0, x + 5y + 2 = 0 +
83. Найдите координаты точки K пересечения прямой
с плоскостью 2x+ 5y- 3z= 0-
+
84. Укажите уравнение окружности, проходящей через точку (4; 5) с центром в точке (1; -3)
-
(x - 1)2 + (y + 3)2 = 73 +
85. Найдите координаты точки пересечения прямых 2x-y- 3 = 0 и 4x+ 3y- 11 = 0
-
(2; 1) +
86. Найдите уравнение прямой, проходящей через точки M1(3; 2), M2(4;-1)
-
3x + y - 11 = 0 +
87. Уравнение 3x - 4y + 12 = 0 преобразуйте к уравнению в отрезках
-
+
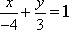88. Определите полуоси гиперболы
-
a= 4, b= 1 +
89. Укажите уравнение окружности, для которой точки А(3; 2) и В(-1; 6) являются концами одного из диаметров
-
(x - 1)2 + (y - 4)2 = 8 +
90. Укажите уравнение параболы с вершиной в точке O и фокусом F(4;0)
-
y2 = 16x +
91. Определите полуоси гиперболы 25x2 - 16y2 = 1
-
+
92. Даны прямые
и 
При каком значении α они перпендикулярны?-
α = 2 +
93. Составьте уравнение плоскости, проходящей через параллельные прямые
и 
-
6x - 20y - 11z + 1 = 0 +
94. При каком положительном значении параметра t прямые, заданные уравнениями 3tx - 8y + 1 = 0 и (1 + t) x - 2ty = 0, параллельны?
-
2 +
95. Какое из перечисленных чисел является иррациональным?
-
3,141592... +
96. Определитель системы трех линейных неоднородных уравнений с тремя неизвестными равен 5. Это означает, что
-
система имеет единственное решений +
97. Укажите уравнение окружности, которая проходит через точку А(3;1), а ее центр лежит на прямой 3x-y- 2 = 0
-
(x - 2)2 + (y - 4)2 = 10 +
98. Определите уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости
-
x – y + 3z – 11 = 0 +
99. Определите эксцентриситет равносторонней гиперболы
-
+
100. Укажите уравнение окружности, которая проходит через точку А(2;6) и ее центр совпадает с точкой C(-1; 2)
-
(x + 1)2 + (y - 2)2 = 25 +