Файл: В настоящее время грп широко применяется в ооо рнюганскнефтегаз как в низкопроницаемых, так и в высокопроницаемых пластахколлекторах.doc

Стимулирование скважины повышает коэффициент продуктивности. Поэтому рассматривать любой вид стимуляции как способ уменьшения скин-эффекта. Из-за столь многочисленных отрицательных сторон скин-эффекта, можно использовать даже способы стимуляции, не только устраняющие повреждение, но и пролагающие новые и расширяющие старые каналы течения. В последнем случае более правильно говорить о псевдоскин-эффекте, показывая, что обработка производит некоторые структурные изменения в канале течения жидкости, вдобавок к устранению закупорки.

Коэффициент продуктивности квазистационарного состояния является очень важным с точки зрения проектирования гидроразрыва:

(1-5)

где J_Dназывается безразмерным коэффициентом продуктивности.

Для скважины, расположенной в центре круговой площади дренирования, выражение для безразмерного коэффициента продуктивности в переходном состоянии сокращается до:

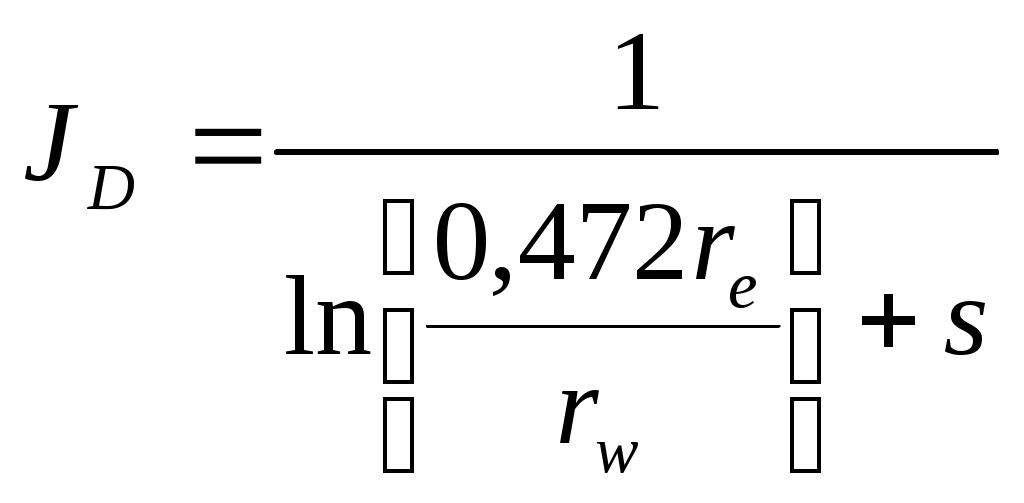(1-6)

В случае расклиненной трещины существуют несколько способов включения эффекта стимуляции в выражение для коэффициента продуктивности. Один из них – использование понятия псевдоскин-эффекта.

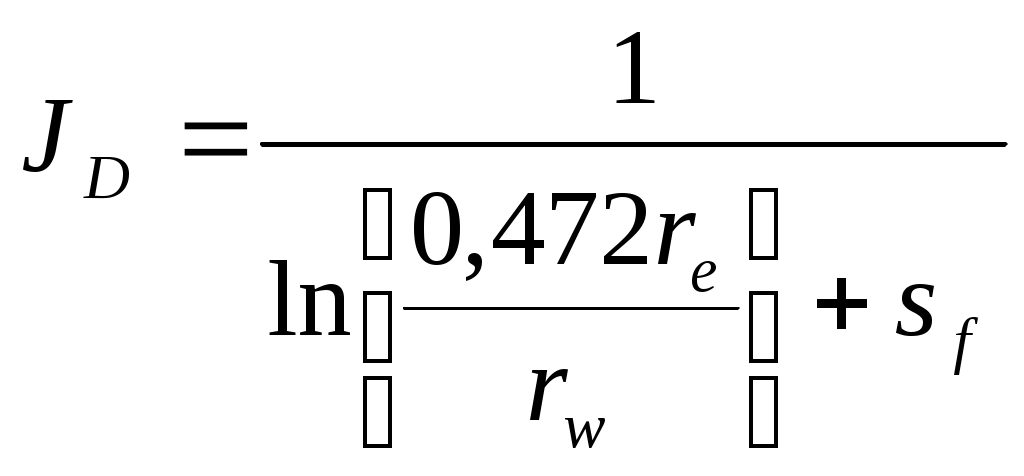(1-7)

или понятия эквивалентного радиуса скважины,

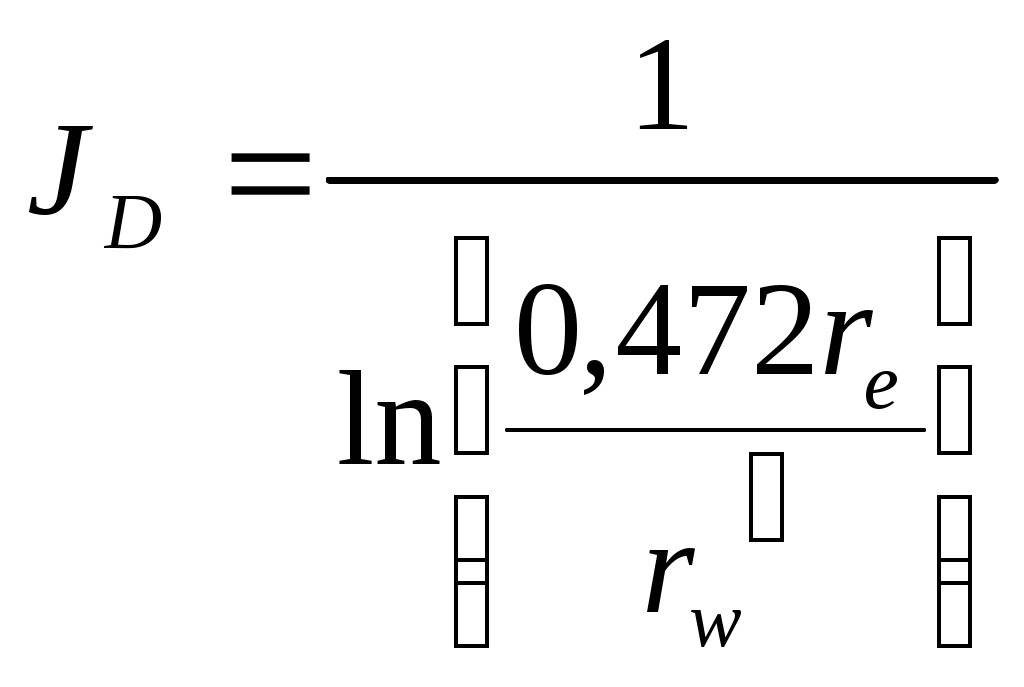(1-8)

или же необходимо просто представить безразмерный коэффициент продуктивности как функцию от параметров трещины,

JD =	Функция от геометрических параметров дренируемой площади и параметров трещины

Все три приведенных выше возможности приводят к примерно одинаковым результатам (если рассчитываются в одинаковых условиях). Последний способ наиболее удобен при рассмотрении скважин с более сложной областью дренирования (не радиальной).

Система скважина-трещина-пласт.
Рассматриваем проникающую на всю глубину трещину в продуктивном слое толщины h, как показано на рис. 1-1.

В реальности площадь дренирования не является ни круглой, ни прямоугольной; однако для большинства из них эти формы являются достаточной аппроксимацией. Использование

---

r_e или x_e – дело личного предпочтения. Соотношение между площадью дренирования А, радиусом дренирования r_e и длиной боковой стороны x_e задается уравнением

(1-10)



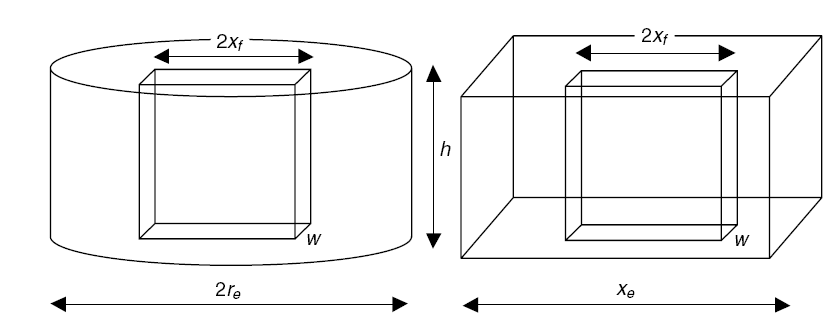
Рисунок 1-1. Обозначения для характеристики трещины.
Характеристики вертикальной скважины, пересекающей прямоугольную вертикальную трещину, которая проходит вертикально по всему объему дренирования, зависят от степени проникновения в направлении x,

(1-11)

и от безразмерной проводимости трещины,

(1-12)

где x_f – половинная длина трещины, x_e – длина стороны прямоугольной области дренирования, k – проницаемость породы, k_f – проницаемость проппанта, и w – средняя ширина расклиненной трещины.

Проппантовое число
Основой для формулировки технической проблемы по оптимизации будет следующий факт: проникновение в трещину и безразмерная проводимость трещины (в горизонтальном направлении) зависят от одного и того же ресурса − количества проппанта. После того, как свойства пласта и расклинивающего агента установлены, нужно найти необходимое соотношение между длиной и шириной трещины. Доступное количество проппанта накладывает ограничения на два безразмерных числа. Чтобы избежать связанных с этим затруднений, вводим безразмерное проппантовое число.

(1-13)

Как показано выше, проппантовое число – это комбинация двух других безразмерных параметров: степени проникновения и безразмерной проводимости трещины. Подставив уравнения, характеризующие эти параметры, в Уравнение 1-13, получаем

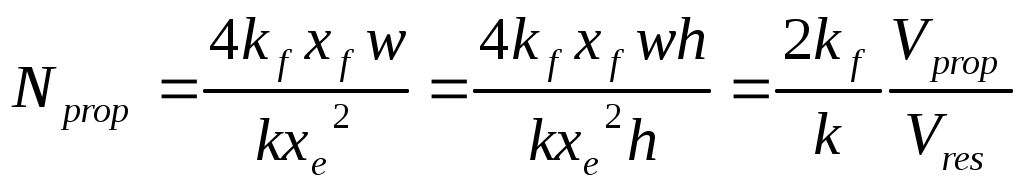(1-14)

где N_prop – коэффициент проппанта; k_f – эффективная проницаемость упакованного проппанта, мД; V_prop – это объем проппанта в продуктивном горизонте (два крыла, включая пустые промежутки между гранулами), фут³; и V_res – объем дренирования (т.е. площадь дренирования, умноженная на толщину слоя), фут

---

³. Уравнение 1-14 это отношение общего объема расклиненной трещины к объему пласта, причем коэффициент пропорциональности составляет удвоенное отношение проницаемостей расклинивающего агента и породы. Учитывается только проппант, находящийся в продуктивном слое. Если, высота трещины в три раза превышает общую толщину слоя, тогда V_prop можно оценить как одну треть общего объема расклинивающего агента. Упакованный объем введенного расклинивающего агента, умноженный на объемную эффективность проппанта дает V_prop, используемый для вычисления проппантового числа.

Безразмерное проппантовое число, N_prop, по-видимому, является наиболее важным параметром в унифицированном проектировании гидроразрыва.

Рис. 1-2 представляет J_D, показанный в обычном виде, как функция от безразмерной проводимости трещины, C_fD; I_x берется как параметр.



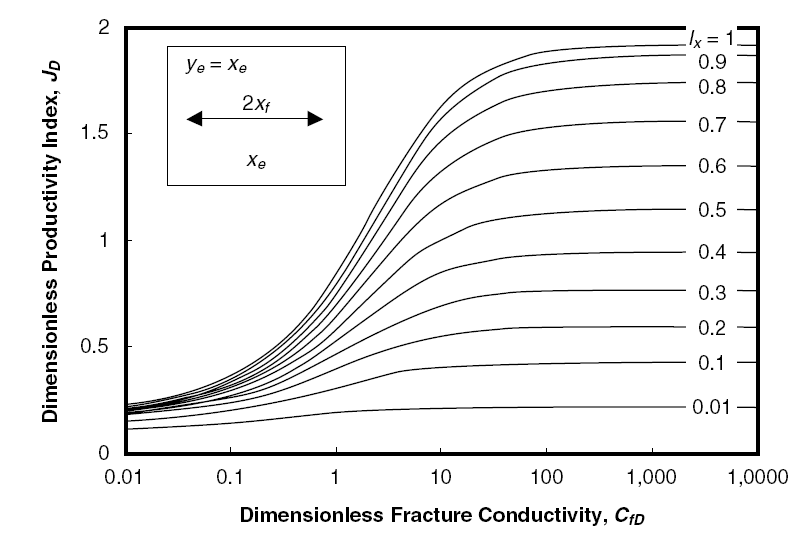
Рисунок 3-2. Безразмерный коэффициент продуктивности как функция от безразмерной проводимости трещины. I_x является параметром (в представлении МакГуайра-Сикоры (McGuire-Sikora)).
На рис. 1-3 и 1-4 аналогичные результаты, параметром является проппантовое число, N_prop. Отдельные кривые соответствуют J_D при определенных значениях коэффициента.

Рис. 1-3 и 1-4, для данного значения N_prop, максимальный коэффициент продуктивности достигается при определенном значении безразмерной проводимости трещины. Проппантовое число характеризует определенный объем, достигающий продуктивного горизонта, оптимальное соотношение между длиной и шириной достигается при значениях безразмерной проводимости трещины, соответствующих пикам кривых.

Важным результатом, полученных из рисунков, является тот факт, что для проппантовых чисел меньших 0,1 оптимальное соотношение находится при C_fD=1,6. Когда объем проппанта возрастает, оно смещается в сторону увеличения, просто потому что безразмерный коэффициент проникновения не может превышать единицы (т.е. когда трещина достигает границ пласта, добавочное количество проппанта направляется на увеличение ширины). Эффект показан на рис. 1-4. Максимально достижимым значением безразмерного коэффициента продуктивности, является 1,909. Максимальное значение КП, равное 6/, относится к идеальному поступательному течению в квадратном пласте.

---

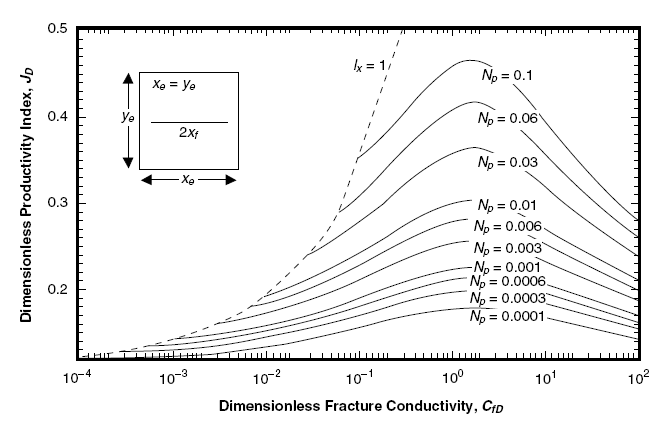
Рисунок 1-3. Безразмерный коэффициент продуктивности как функция от безразмерной проводимости трещины, где коэффициент проппанта является параметром (для N_prop < 0,1).



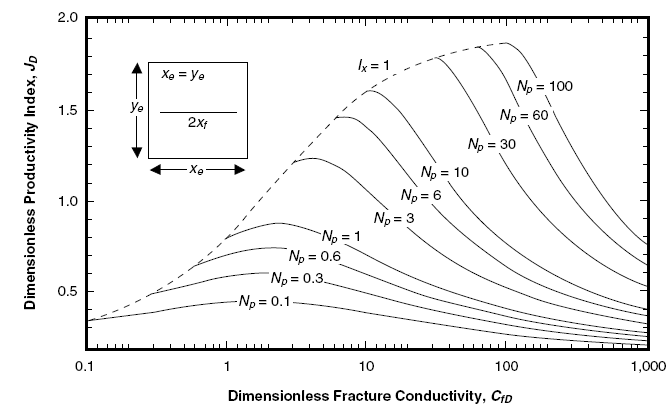
Рисунок 1-4. Безразмерный коэффициент продуктивности как функция от безразмерной проводимости трещины, где коэффициент проппанта является параметром (для N_prop > 0,1).
В средне- и высокопроницаемых породах (более 50 мД), невозможно достичь значения проппантового числа более 0,1. Для обработки ВПР, типичные его значения заключаются в интервале 0,0001 – 0,01. Таким образом, для средне- и высокопроницаемых пород, лучшим значением безразмерной проводимости трещины является 1,6.

В пластах «сжатого газа» принципиально возможно достижение высоких значений коэффициента проппанта. Коэффициенты вычисляются для ограниченной площади дренирования, и могут составлять от 1 до 10; не определяется реально содержащееся в продуктивном слое количество проппанта. Однако на практике проппантового числа выше 1 достичь достаточно трудно. При массированных обработках проппант может мигрировать вверх, приводя к чрезмерному незапланированному увеличению высоты трещины; или же может по горизонтали выходить за пределы дренируемой области.



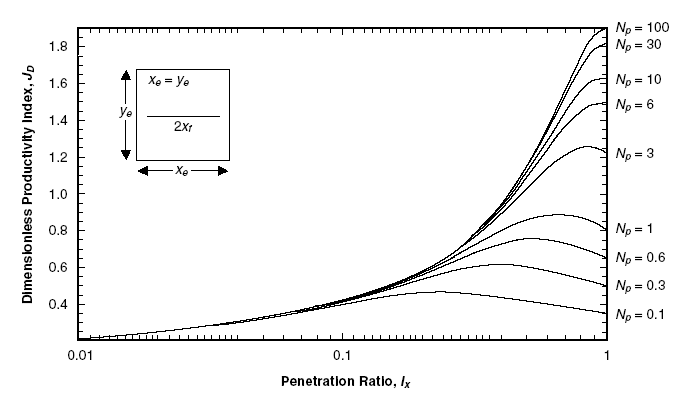
Рисунок 1-5. Безразмерный коэффициент продуктивности как функция от степени проникновения, где проппантовое число является параметром (для N_prop > 0,1).
Для высоких значений числа оптимальное значение C_fD определяет оптимальную степень проникновения, близкую к 1. Этот факт проиллюстрирован на рис. 1-5, где степень проникновения откладывается по оси х. Чтобы разместить проппант «от стенки до стенки», сохраняя его в дренируемом объеме, необходима настолько высокая тщательность в проведении гидроразрыва, что ее практически невозможно достичь.

Максимально возможным значением безразмерного коэффициента продуктивности при N_prop=1 является J_D около 0,9. Для вертикальной скважины при отсутствии повреждения J_D составляет от 0,12 до 0,14, в зависимости от размещения скважины и от ее радиуса проводимости. Существует реальный предел для роста коэффициента продуктивности квазистационарного состояния (при условии нулевого скин-эффекта), например отношение 0,9 к 0,13 составляет около 7. Более значительное увеличение не характерно. Его можно достигнуть при условии наличия в исходной скважине большого положительного скин-фактора.

---

При неустановившемся течении коэффициент продуктивности (а также производительность) выше, чем для квазистационарного состояния. Наличие периода неустановившегося течения не меняет решения по оптимальным размерам. Вычисления показывают, что нет причины отказываться от оптимальных значений, полученных в переходном состоянии, если скважина будет работать в этом режиме значительное время.

В определении проппантового числа k_f есть эффективная (или эквивалентная) проницаемость закрепленного проппанта. Этот параметр будет основным при планировании. Современные симуляторы трещин обычно используют номинальные значения для проницаемости упакованного проппанта (данные от производителя) и позволяют пропорционально уменьшить его с помощью коэффициента уменьшения. Уменьшенное значение и необходимо использовать при вычислении проппантового числа.

Существуют многочисленные причины для того, что реальная проницаемость проппанта будет меньшей, чем номинальное значение. Основными являются следующие:

• 
  Высокое давление закрытия разрушает проппант, уменьшая средний размер зерна, однородность зерен и пористость.
  
• 
  Остаток жидкости разрыва понижает проницаемость в трещине.
  
• 
  Высокая скорость движения жидкости в слое проппанта приводит к нарушению закона Дарси, что в свою очередь выражается в дальнейших потерях давления. Это явление может оказать значительное влияние, когда газ добывается в присутствии жидкости (воды или конденсата). Неподчинение закону Дарси происходит из-за периодического ускорения-замедления капель жидкости, что значительно понижает проницаемость проппанта. Полученная проницаемость может быть на порядок ниже номинального значения, заявляемого производителем.
  

В процессе проектирования гидроразрыва, значительное внимание следует уделить эффективной проницаемости проппанта и проницаемости породы. Знание соотношения этих параметров очень важно и не может быть заменено другими количественными отношениями.
Поведение скважин при средних и малых значениях проппантового числа
Под малыми и средними проппантовыми числами, подразумеваем значения менее 0,1. В эту категорию попадают наиболее динамичные способы осуществления гидроразрыва (например, ВПР), что делает ее очень важной с точки зрения проектирования.

Оптимальный план обработки для средних значений проппантовых чисел можно кратко и просто представить в аналитическом виде. Далее мы рассмотрим, как проппантовое число и безразмерный коэффициент продуктивности соотносятся с другими распространенными индексами эффективности, такими как

---