Файл: В настоящее время грп широко применяется в ооо рнюганскнефтегаз как в низкопроницаемых, так и в высокопроницаемых пластахколлекторах.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 130
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
псевдоскин-функция Синко-Лей (Cinco-Ley) и Саманьеджо (Samaniego), а также эквивалентный радиус скважины Пратса. На самом деле, планирование гидроразрыва, основанное на этих коэффициентах, является частным случаем унифицированного проектирования гидроразрыва, при малых значениях проппантовых чисел.
Пратс (Prats) (1961) ввел понятие эквивалентного радиуса скважины, исходя из операции гидроразрыва. Все переменные кроме протяженности трещины, влияют на характеристики скважины только через комбинированную величину – безразмерную проводимость трещины. При высоких значениях безразмерной проводимости (более 100) ее свойства аналогичны свойствам трещины с бесконечной проводимостью. Поведение трещин с бесконечной проводимостью было впоследствии изучено Грингартеном (Gringarten) и Реми (Remi) (1974). Чтобы охарактеризовать влияние ограниченно-проводящей вертикальной трещины на характеристики вертикальной скважины, Синко-Лей и Саманьеджо (1981) ввели понятие псевдоскин-эффекта, который является функцией исключительно от безразмерной проводимости трещины.
Судя по определению псевдоскин-эффекта, безразмерный коэффициент квазистационарного состояния может быть представлен следующим образом
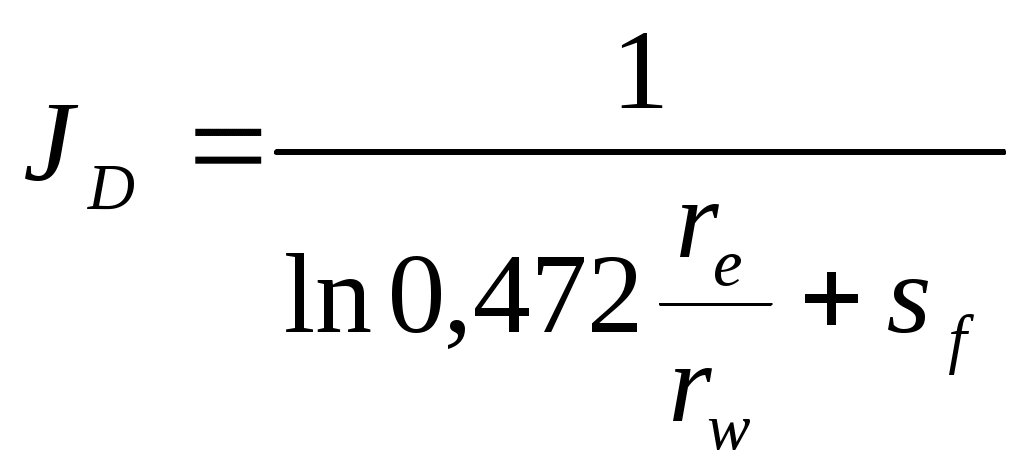(1-15)
где sf – эффект псевдоскина. В представлении Пратса тот же коэффициент продуктивности описывается так:
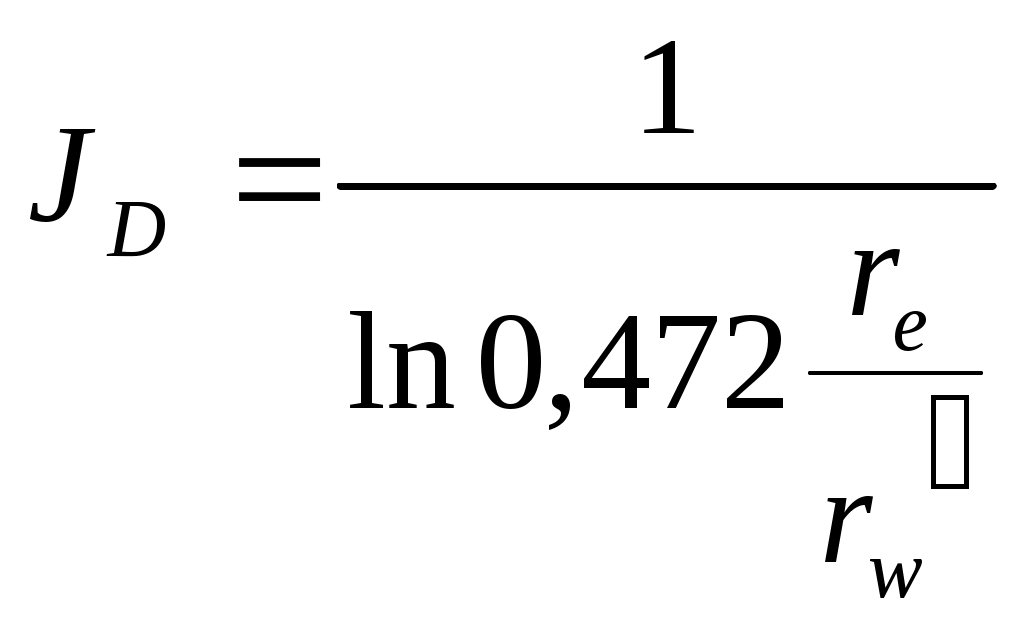(1-16)
где rw'– эквивалентный радиус скважины. Пратс использовал также относительный эквивалентный радиус скважины, определяющийся как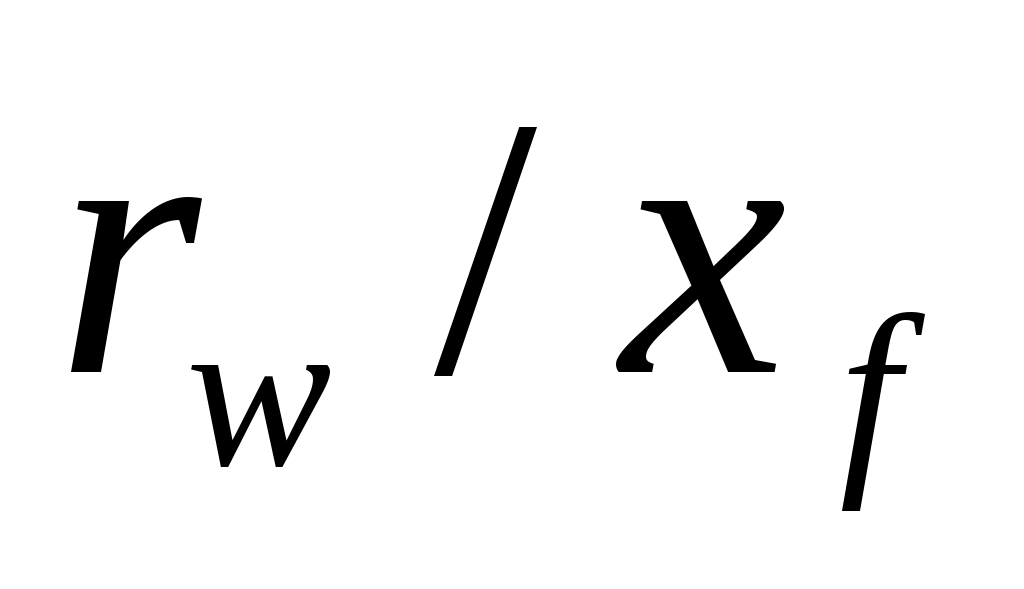
.
С точки зрения Синко-Лея формально коэффициент продуктивности описывается так:
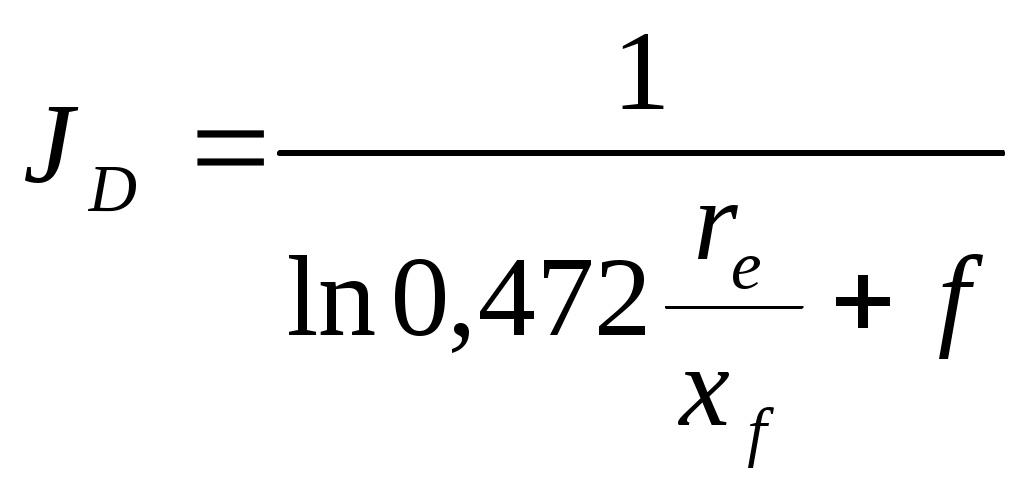(1-17)
где f – псевдоскин-функция по отношению к половинной длине трещины.
В таблице 3-2 приведены соотношения между этими величинами.
Преимущества нотации Синко-Лея и Саманьеджо (f-фактор) заключается в том, что для средних и малых значений проппантовых чисел величина fзависит только от безразмерной проводимости трещины. Сплошная линия на рис. 1-6 отображает f-фактор как функцию от безразмерной проводимости трещины.
При высоких значениях CfD, выражение для f-фактора стремится к значению ln2, показывая, что продукция из бесконечно проводящей трещины в /2 раз больше, чем от той же самой поверхности, расположенной цилиндрически. В вычислениях удобно использовать расширенное выражение для переменной.
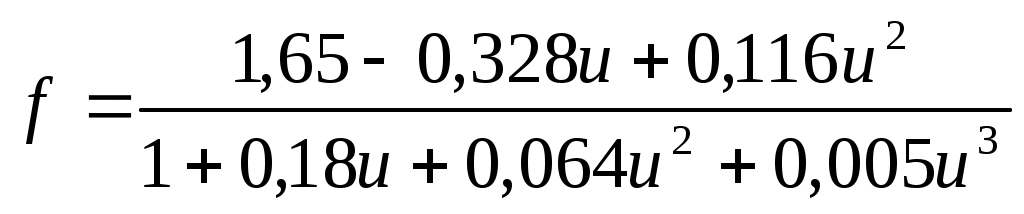, где u=lnCfD (1-18)
Так как относительный радиус скважины Пратса может быть выражен через f-фактор (см. Таблицу 3-2), мы получаем аналогичный результат:
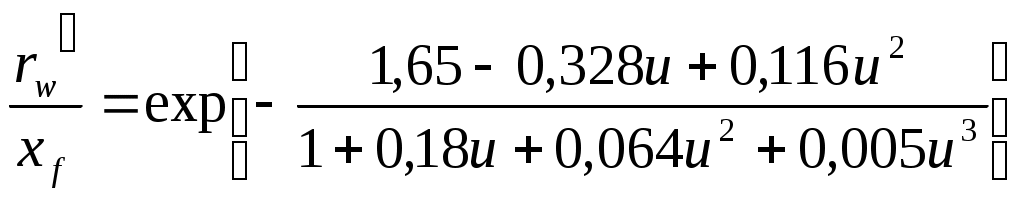, где u=lnCfD (1-19)
Кривые, соответствующие уравнениям 1-18 и 1-19 являются действительными только в промежутке, показанном на рис. 3-6. Для очень больших значений CfD можно просто использовать предельное значение уравнения 1-19, равное 0,5; это показывает, что бесконечно проводящая трещина имеет продуктивность, одинаковую со скважиной, имеющей радиус xf/2.
Таблица 1-2. Соотношения между различными индексами продуктивности.
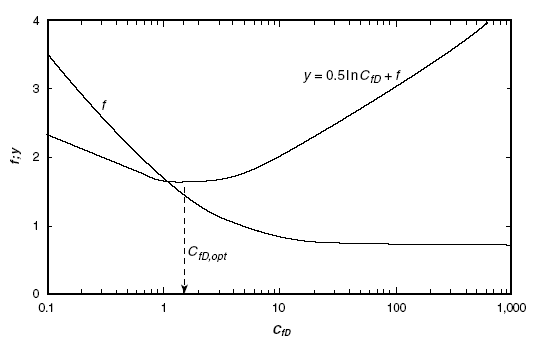
Рисунок 1-6. f-фактор и y-функция Синко-Лей и Саманьеджо.
Оптимальная проводимость трещины.
Nprop < 0,1 можно сформулировать чисто физическую проблему по оптимизации: каким образом можно выбрать длину и ширину, если объем проппанта в одном из крыльев трещины Vf=w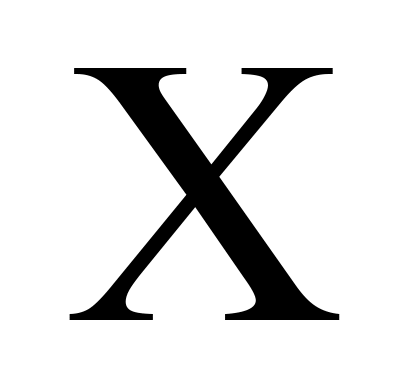
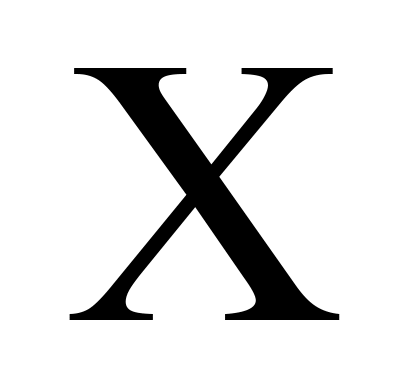h xf ограничен, причем существует необходимость максимизировать коэффициент продуктивности в переходном режиме течения. Толщина породы, радиус дренирования и проницаемости породы и проппанта известны, и что трещина вертикально полностью проницаема (
hf=h).
Взяв CfD в качестве основной переменной, длину можно выразить как
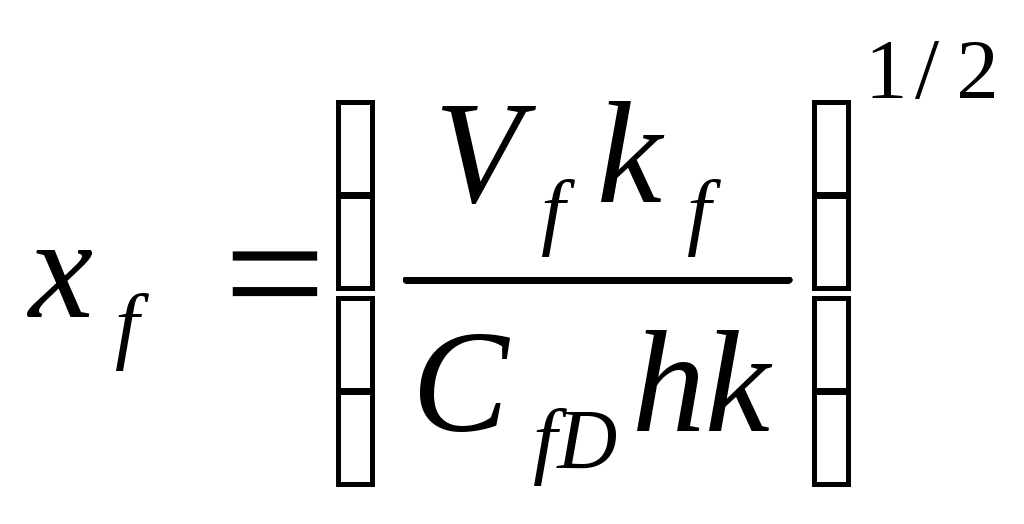(1-21)
Подставив уравнение 1-21 в уравнение 1-17, можно выразить безразмерный коэффициент продуктивности:
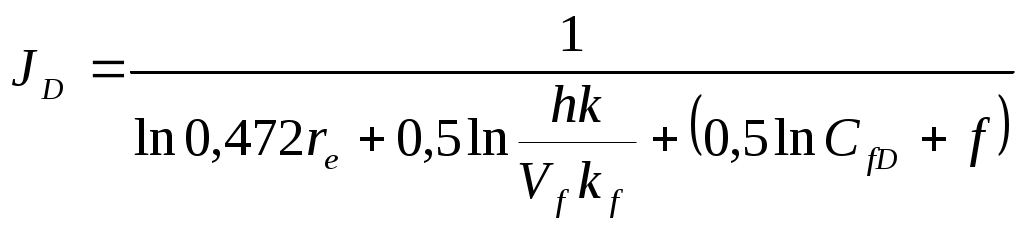(1-22)
где единственной неизвестной является CfD. Так как радиус дренирования, толщина породы, проницаемости и объем проппанта фиксированы, коэффициент продуктивности является максимальным, когда выражение в скобках
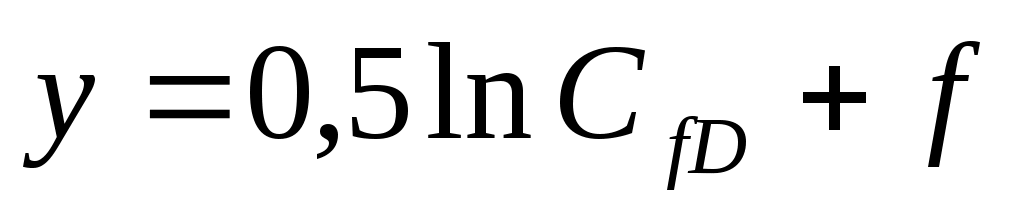(1-23)
достигает своего минимума. Эта зависимость также показана на рис. 1-6. Так как оно зависит только от CfD, оптимальное CfDopt=1,6 является постоянной величиной для любого пласта, скважины и объема проппанта.
Пласт и трещина могут рассматриваться как единая система. Пласт может подать больший объем жидкости в трещину, если ее длина больше, однако (так как объем фиксирован), это означает уменьшение ее ширины. В узкой трещине сопротивление течению может быть значительным. Оптимальная безразмерная проводимость трещины характеризует наилучшее соотношение между двумя вышеуказанными подсистемами. После нахождения этого соотношения из определения CfD можно рассчитать половинную длину трещины,
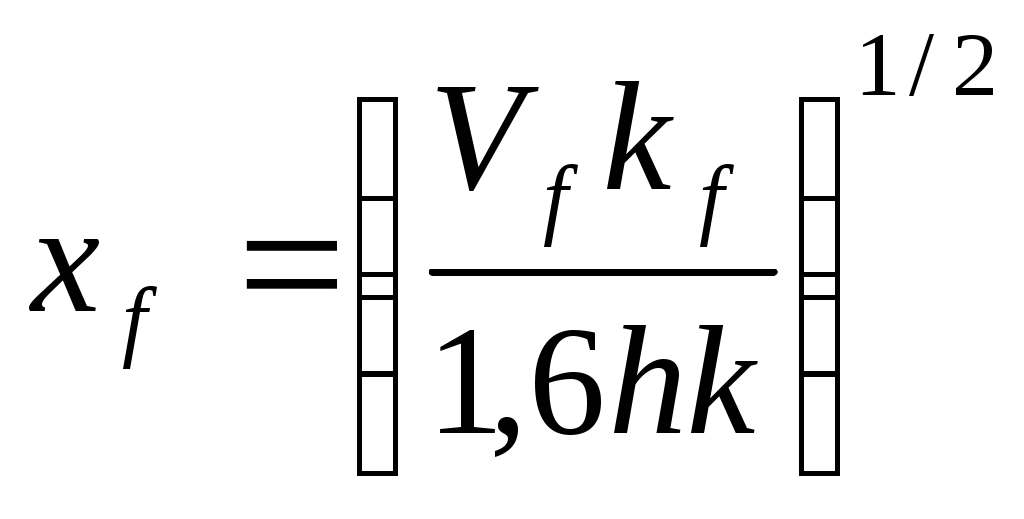(1-24)
и следовательно среднее значение ширины будет определяться как
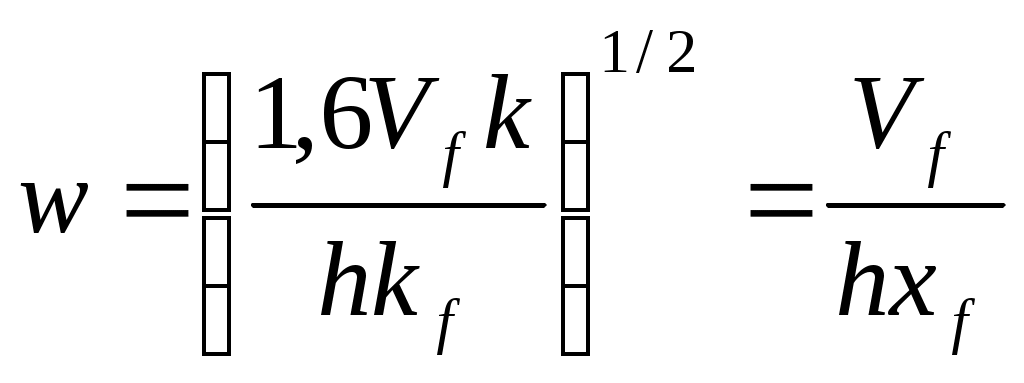(1-25)
Отметим, что Vf есть Vprop/2, так как это только половина проппанта (одно из крыльев трещины).
Наиболее важный вывод из всех вышеописанных результатов следующий: теоретически нет различий между гидроразрывом высоко- и низкопроницаемых пластов. Во всех случаях существует трещина с оптимальными характеристиками, имеющая CfD около единицы. В низкопроницаемых породах это требование приводит к узким и длинным трещинам, а в высокопроницаемых – к широким, но коротким. Однако они имеют одну и ту же безразмерную проводимость.
Если длина трещины и ее ширина выбираются согласно оптимальному соотношению, безразмерный коэффициент продуктивности будет выражаться как
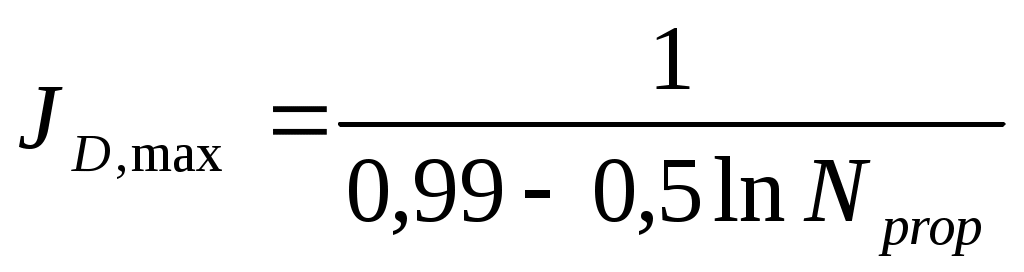(1-26)
Оптимальные характеристики трещины могут быть технически или экономически недостижимы. В низкопроницаемых породах указанная длина трещины может быть слишком велика; или же очень малая ширина трещины может означать, неприменимость принятого коэффициента проницаемости проппанта. В высокопроницаемых породах не всегда можно создать трещину большой ширины. Безразмерная проводимость трещины, сильно отличающаяся от оптимальной, показывает, что или трещина является «узким местом» (CfD<<1,6), или же она слишком «широкая и короткая» (CfD>>1,6).
Читателю также не следует забывать, что результаты этого раздела, включающие в себя график Синко-Лея и Саманьеджо с рассчитанной кривой, значение оптимальной безразмерной проводимости трещины, равное 1,6 и Уравнение 1-26 действительны только для проппантовых чисел, меньших 0,1. Это можно легко увидеть, сравнив рис. 1-3 и 1-4. На рис. 1-3 кривые имеют максимум при CfD=1,6, и максимум JD соответствует простому уравнению 1-26. На рис. 1-4, при проппантовых числах больших 0,1, максимумы смещены, и упрощенные вычисления, основанные на f-факторе (Уравнение 1-18) или эквивалентном радиусе (Уравнение 1-19) недействительны.
Логика планирования.
Необходимо поместить определенное количество проппанта в продуктивный слой таким образом, чтобы достичь максимального значения коэффициента продуктивности. Ключевым параметром при определении соотношения между размером и повышением продуктивности является проппантовое число. Так как Vprop составляет только часть расклинивающего агента, достигающего продуктивной области, и таким образом зависит от объемной эффективности проппанта, проппантовое число не может просто быть принято постоянным в ходе планирования.
В унифицированном проектировании гидроразрыва указываем количество проппанта, предназначенного к закачке, и далее производим следующие операции:
1. Получить объемную эффективность проппанта и определить проппантовое число. (Как только появятся детали обработки, соотношение объемной эффективности и высоты трещины, процесс планирования может быть повторен.)
2. Используя рис. 1-3 или 1-4 (или скорее схему планирования), определить максимально возможный коэффициент продуктивности, а также оптимальную безразмерную проводимость трещины, исходя из проппантового числа.
3. Рассчитать оптимальную половинную длину трещины. Рассматривая объем одного из крыльев трещины (внутри продуктивного слоя) как Vf, оптимальную половинную длину можно определить как:
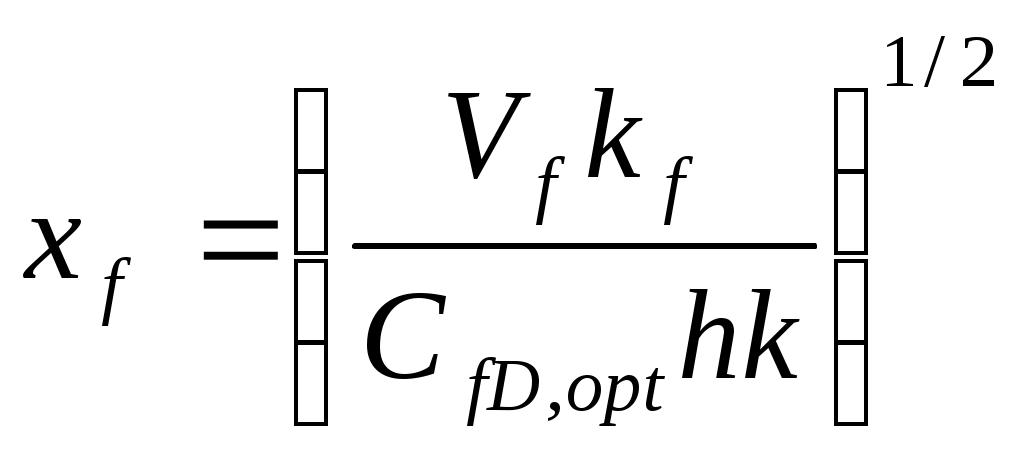(1-27)
4. Рассчитать оптимальную усредненную ширину расклиненной трещины
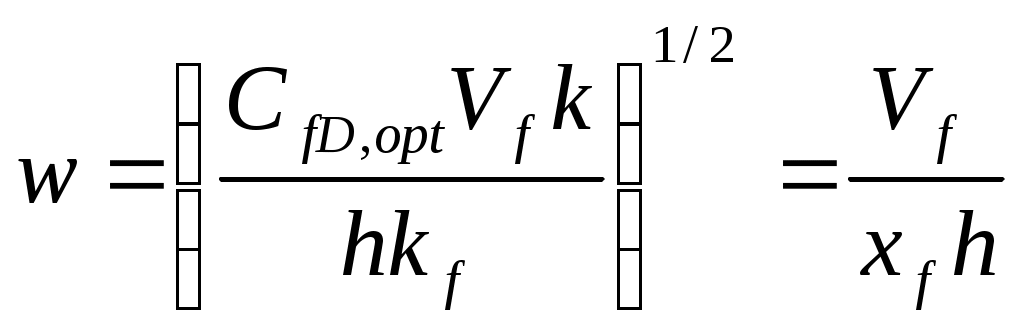(1-28)
В двух вышеуказанных уравнениях Vf и h должны соответствовать друг другу. Если h используется для общей высоты трещины, часто обозначаемой как hf, тогда объем проппанта Vfдолжен являться общим объемом проппанта в одном из крыльев трещины. В то же время, если выбранный Vf соответствует только объему, содержащемуся в продуктивной зоне одного из крыльев, тогда h должно являться толщиной продуктивного слоя. В обоих случаях результат будет одинаковым. Наиболее удобно использовать толщину продуктивного слоя и объем проппанта в продуктивном слое, так как эти переменные используются в процессе вычисления проппантового числа.
Пратс (Prats) (1961) ввел понятие эквивалентного радиуса скважины, исходя из операции гидроразрыва. Все переменные кроме протяженности трещины, влияют на характеристики скважины только через комбинированную величину – безразмерную проводимость трещины. При высоких значениях безразмерной проводимости (более 100) ее свойства аналогичны свойствам трещины с бесконечной проводимостью. Поведение трещин с бесконечной проводимостью было впоследствии изучено Грингартеном (Gringarten) и Реми (Remi) (1974). Чтобы охарактеризовать влияние ограниченно-проводящей вертикальной трещины на характеристики вертикальной скважины, Синко-Лей и Саманьеджо (1981) ввели понятие псевдоскин-эффекта, который является функцией исключительно от безразмерной проводимости трещины.
Судя по определению псевдоскин-эффекта, безразмерный коэффициент квазистационарного состояния может быть представлен следующим образом
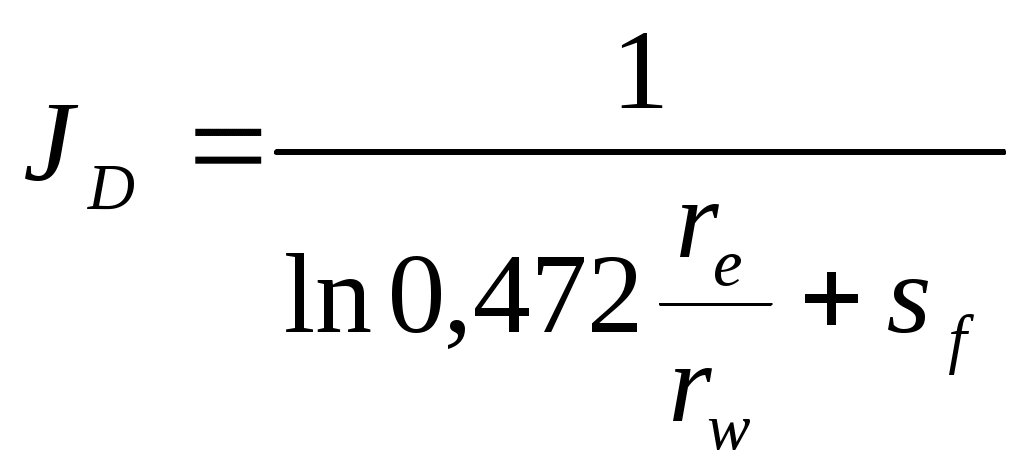(1-15)где sf – эффект псевдоскина. В представлении Пратса тот же коэффициент продуктивности описывается так:
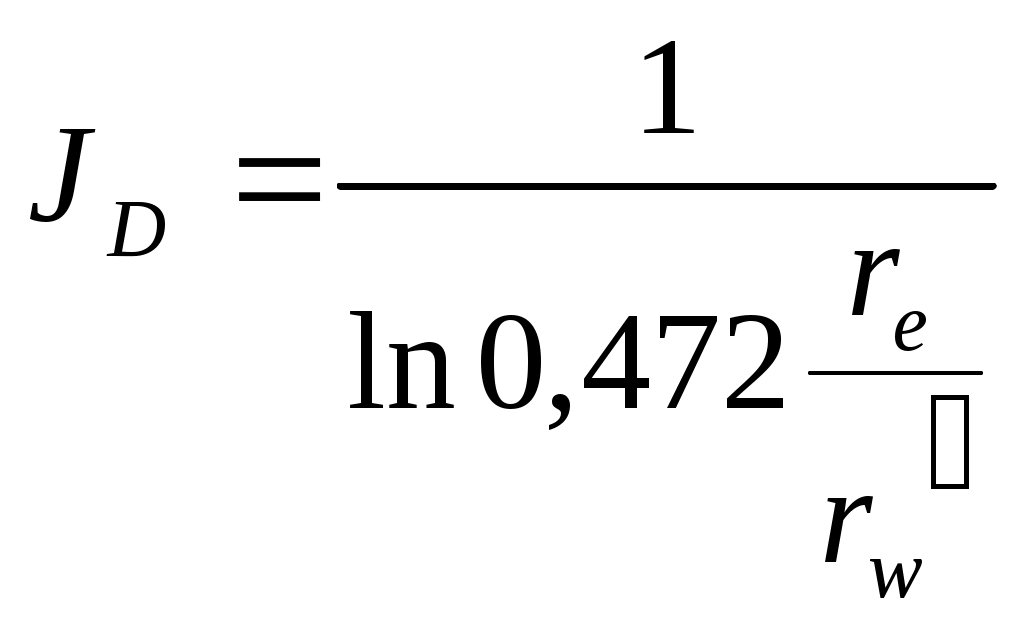(1-16)где rw'– эквивалентный радиус скважины. Пратс использовал также относительный эквивалентный радиус скважины, определяющийся как
. С точки зрения Синко-Лея формально коэффициент продуктивности описывается так:
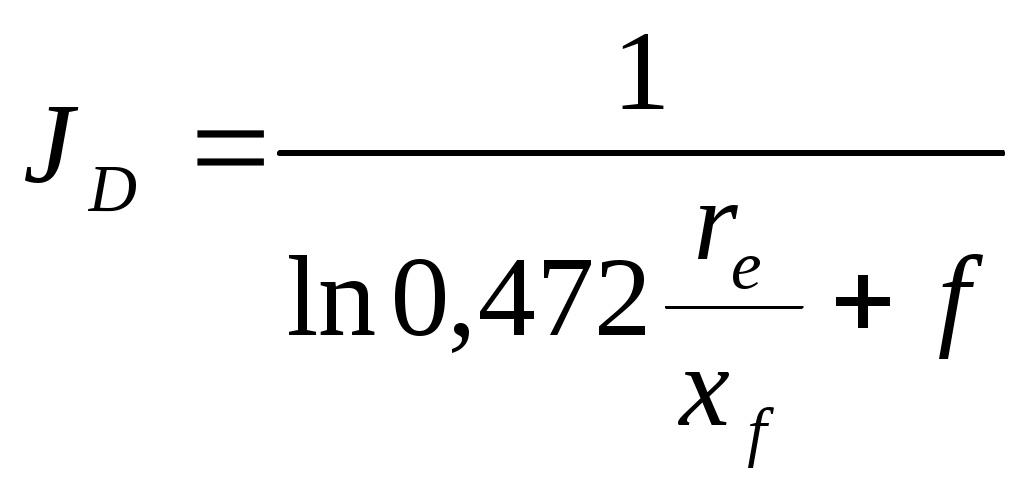(1-17)где f – псевдоскин-функция по отношению к половинной длине трещины.
В таблице 3-2 приведены соотношения между этими величинами.
Преимущества нотации Синко-Лея и Саманьеджо (f-фактор) заключается в том, что для средних и малых значений проппантовых чисел величина fзависит только от безразмерной проводимости трещины. Сплошная линия на рис. 1-6 отображает f-фактор как функцию от безразмерной проводимости трещины.
При высоких значениях CfD, выражение для f-фактора стремится к значению ln2, показывая, что продукция из бесконечно проводящей трещины в /2 раз больше, чем от той же самой поверхности, расположенной цилиндрически. В вычислениях удобно использовать расширенное выражение для переменной.
, где u=lnCfD (1-18)Так как относительный радиус скважины Пратса может быть выражен через f-фактор (см. Таблицу 3-2), мы получаем аналогичный результат:
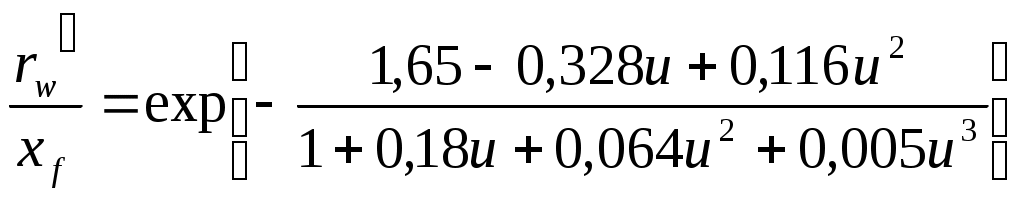, где u=lnCfD (1-19)Кривые, соответствующие уравнениям 1-18 и 1-19 являются действительными только в промежутке, показанном на рис. 3-6. Для очень больших значений CfD можно просто использовать предельное значение уравнения 1-19, равное 0,5; это показывает, что бесконечно проводящая трещина имеет продуктивность, одинаковую со скважиной, имеющей радиус xf/2.
Таблица 1-2. Соотношения между различными индексами продуктивности.
 |  |
 |  |
 |  |
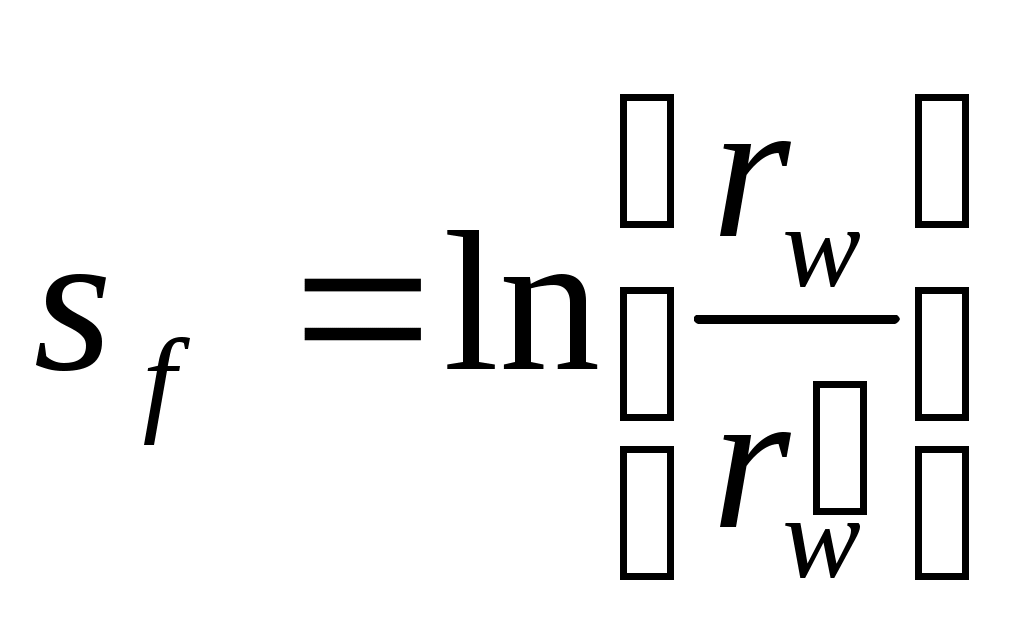Рисунок 1-6. f-фактор и y-функция Синко-Лей и Саманьеджо.
Оптимальная проводимость трещины.
Nprop < 0,1 можно сформулировать чисто физическую проблему по оптимизации: каким образом можно выбрать длину и ширину, если объем проппанта в одном из крыльев трещины Vf=w
h xf ограничен, причем существует необходимость максимизировать коэффициент продуктивности в переходном режиме течения. Толщина породы, радиус дренирования и проницаемости породы и проппанта известны, и что трещина вертикально полностью проницаема (
hf=h).
Взяв CfD в качестве основной переменной, длину можно выразить как
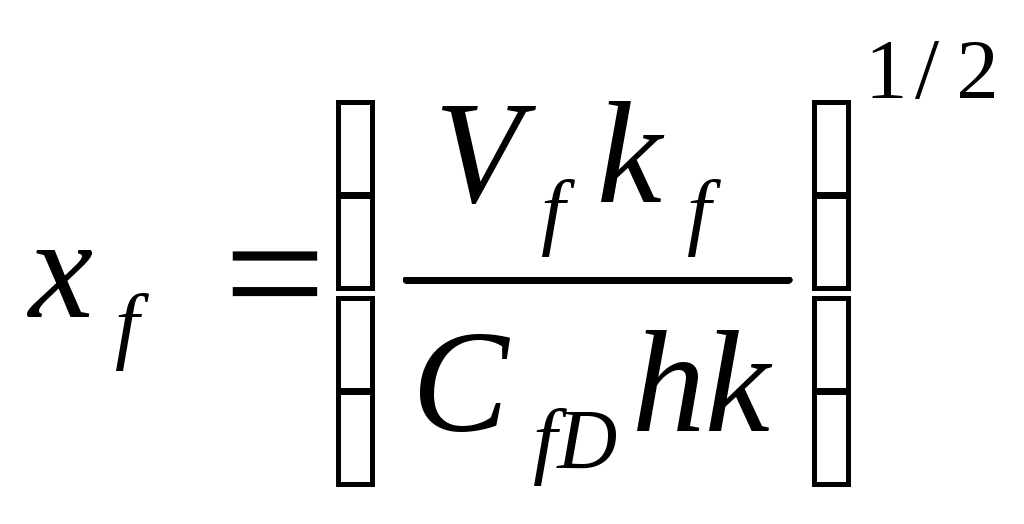(1-21)Подставив уравнение 1-21 в уравнение 1-17, можно выразить безразмерный коэффициент продуктивности:
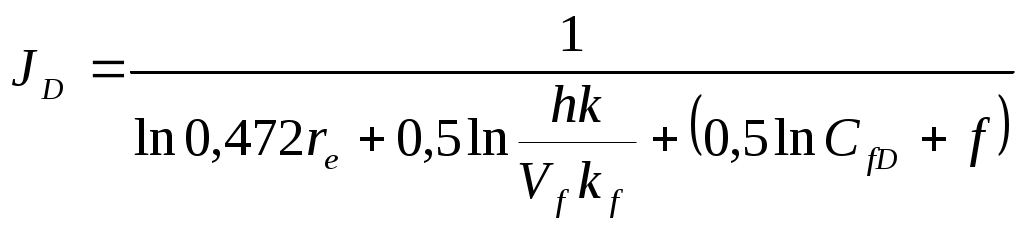(1-22)где единственной неизвестной является CfD. Так как радиус дренирования, толщина породы, проницаемости и объем проппанта фиксированы, коэффициент продуктивности является максимальным, когда выражение в скобках
(1-23)достигает своего минимума. Эта зависимость также показана на рис. 1-6. Так как оно зависит только от CfD, оптимальное CfDopt=1,6 является постоянной величиной для любого пласта, скважины и объема проппанта.
Пласт и трещина могут рассматриваться как единая система. Пласт может подать больший объем жидкости в трещину, если ее длина больше, однако (так как объем фиксирован), это означает уменьшение ее ширины. В узкой трещине сопротивление течению может быть значительным. Оптимальная безразмерная проводимость трещины характеризует наилучшее соотношение между двумя вышеуказанными подсистемами. После нахождения этого соотношения из определения CfD можно рассчитать половинную длину трещины,
(1-24)и следовательно среднее значение ширины будет определяться как
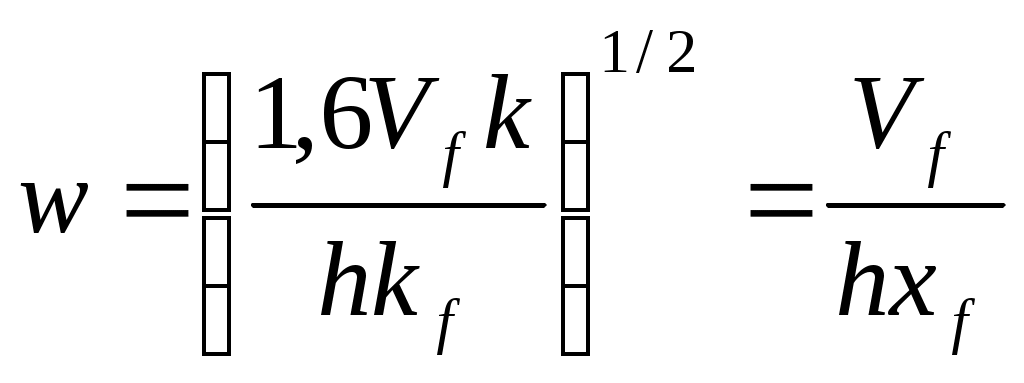(1-25)Отметим, что Vf есть Vprop/2, так как это только половина проппанта (одно из крыльев трещины).
Наиболее важный вывод из всех вышеописанных результатов следующий: теоретически нет различий между гидроразрывом высоко- и низкопроницаемых пластов. Во всех случаях существует трещина с оптимальными характеристиками, имеющая CfD около единицы. В низкопроницаемых породах это требование приводит к узким и длинным трещинам, а в высокопроницаемых – к широким, но коротким. Однако они имеют одну и ту же безразмерную проводимость.
Если длина трещины и ее ширина выбираются согласно оптимальному соотношению, безразмерный коэффициент продуктивности будет выражаться как
(1-26)Оптимальные характеристики трещины могут быть технически или экономически недостижимы. В низкопроницаемых породах указанная длина трещины может быть слишком велика; или же очень малая ширина трещины может означать, неприменимость принятого коэффициента проницаемости проппанта. В высокопроницаемых породах не всегда можно создать трещину большой ширины. Безразмерная проводимость трещины, сильно отличающаяся от оптимальной, показывает, что или трещина является «узким местом» (CfD<<1,6), или же она слишком «широкая и короткая» (CfD>>1,6).
Читателю также не следует забывать, что результаты этого раздела, включающие в себя график Синко-Лея и Саманьеджо с рассчитанной кривой, значение оптимальной безразмерной проводимости трещины, равное 1,6 и Уравнение 1-26 действительны только для проппантовых чисел, меньших 0,1. Это можно легко увидеть, сравнив рис. 1-3 и 1-4. На рис. 1-3 кривые имеют максимум при CfD=1,6, и максимум JD соответствует простому уравнению 1-26. На рис. 1-4, при проппантовых числах больших 0,1, максимумы смещены, и упрощенные вычисления, основанные на f-факторе (Уравнение 1-18) или эквивалентном радиусе (Уравнение 1-19) недействительны.
Логика планирования.
Необходимо поместить определенное количество проппанта в продуктивный слой таким образом, чтобы достичь максимального значения коэффициента продуктивности. Ключевым параметром при определении соотношения между размером и повышением продуктивности является проппантовое число. Так как Vprop составляет только часть расклинивающего агента, достигающего продуктивной области, и таким образом зависит от объемной эффективности проппанта, проппантовое число не может просто быть принято постоянным в ходе планирования.
В унифицированном проектировании гидроразрыва указываем количество проппанта, предназначенного к закачке, и далее производим следующие операции:
1. Получить объемную эффективность проппанта и определить проппантовое число. (Как только появятся детали обработки, соотношение объемной эффективности и высоты трещины, процесс планирования может быть повторен.)
2. Используя рис. 1-3 или 1-4 (или скорее схему планирования), определить максимально возможный коэффициент продуктивности, а также оптимальную безразмерную проводимость трещины, исходя из проппантового числа.
3. Рассчитать оптимальную половинную длину трещины. Рассматривая объем одного из крыльев трещины (внутри продуктивного слоя) как Vf, оптимальную половинную длину можно определить как:
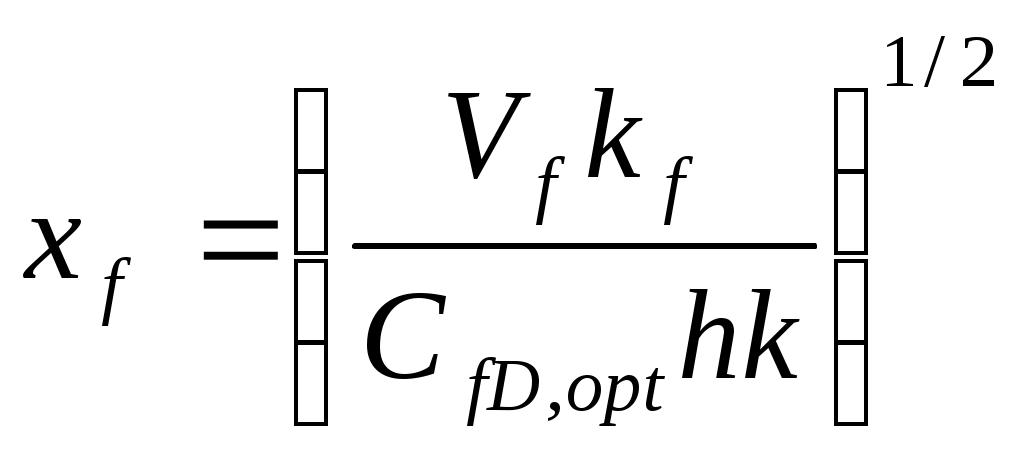(1-27)4. Рассчитать оптимальную усредненную ширину расклиненной трещины
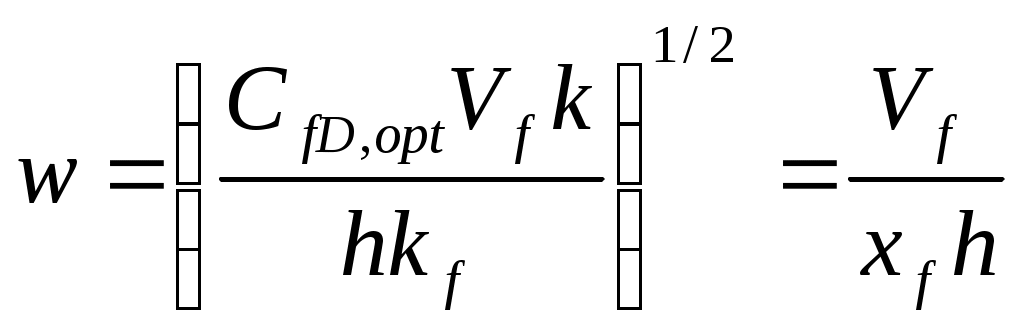(1-28)В двух вышеуказанных уравнениях Vf и h должны соответствовать друг другу. Если h используется для общей высоты трещины, часто обозначаемой как hf, тогда объем проппанта Vfдолжен являться общим объемом проппанта в одном из крыльев трещины. В то же время, если выбранный Vf соответствует только объему, содержащемуся в продуктивной зоне одного из крыльев, тогда h должно являться толщиной продуктивного слоя. В обоих случаях результат будет одинаковым. Наиболее удобно использовать толщину продуктивного слоя и объем проппанта в продуктивном слое, так как эти переменные используются в процессе вычисления проппантового числа.