Практическая работа по теме 2.2 «Знакомство с современными российскими программными решениями на уроках информатики и во внеурочной деятельности»
Название работы: Разработка серии учебных заданий для решения задачи поиска кратчайшего пути в графе на материале геоинформационных систем




Тема занятия: Нахождение кратчайшего пути в графе с помощью алгоритма Дейкстры.

Цель проведения занятия: научиться находить кратчайшие пути в графе с помощью алгоритма Дейкстры.

После выполнения работы студент должен

знать: алгоритма Дейкстры нахождения кратчайшего пути в графе;

уметь: находить пути в графе с помощью алгоритма Дейкстры.

Материально-техническое оснащение рабочего места: инструкционные карты, конспект.

Инструктаж по технике безопасности

Содержание и порядок выполнения задания

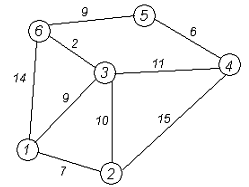
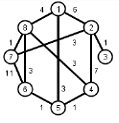
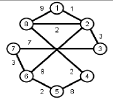
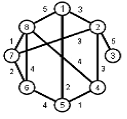
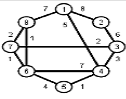
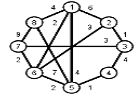
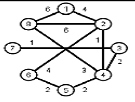
Задание 1. Требуется найти кратчайшие расстояния от 1 -й вершины до всех остальных для графа, представленного на рисунке:


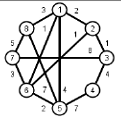
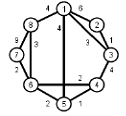
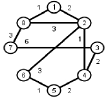
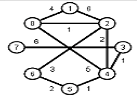
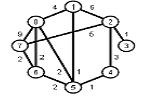
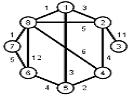
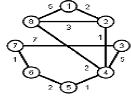
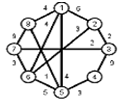
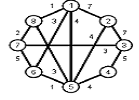
Задани2 ( по вариантам).
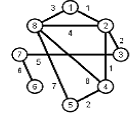
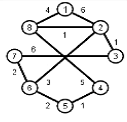
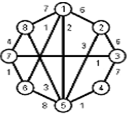
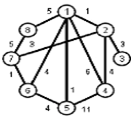
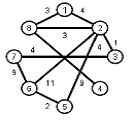
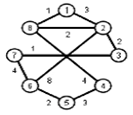
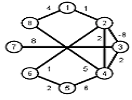
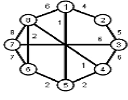
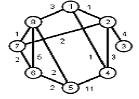
Найти кратчайшие расстояния от 1 -й вершины до всех остальных для графа, представленного на рисунке. (вес ребра брать положительный)

---

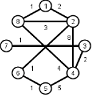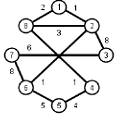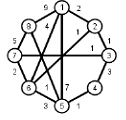Вопросы для самоконтроля:

1. 
   Дайте определение понятию поиск кратчайшего пути?
   
2. 
   Между какими вершинами в графе алгоритм Дейкстры позволяет находить кратчайший путь?
   
3. 
   В чем заключается идея алгоритма поиска пути Дейкстры?
   
4. 
   К какому виду алгоритма поиска пути («в глубину» или «в ширину») относится алгоритм Дейкстры и почему?
   
5. 
   Какое условие должно выполняться для применения алгоритма Дейкстры?
   

Краткие сведения по теоретической части работы

Нахождение кратчайшего пути на сегодняшний день является жизненно необходимой задачей и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до колледжа), в

---

---

Смотрите также файлы

• Договор куплипродажи понятие, содержание и виды.pdf

• Счет лет в истории Урок 2.docx

• Отчет профессиональноориентированной практики за 7 семестр Студент 4 курса группы фо.docx

• Практическая работа 1 по теме Целостный педагогический процесс единство обучения и воспитания Педагогическая задача Контекст решения задачи.docx

• Современные методы контроля стерилизации и дезинфекции в бактериологической лаборатории.docx