Файл: Контрольная работа по дисциплине Математика, 3 семестр 2021 2022 уч г. Вариант 4 Задание 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СЕРВИСА»
(ФГБОУ ВО «ПВГУС»)
Кафедра: « МиЕНД »
КОНТРОЛЬНАЯ РАБОТА
По дисциплине: Математика(3)
вАРИАНТ №4
Работу выполнила
Студент: Гончаров А.Е.
Группа: СПБДз21с
Проверил:
Тольятти 2021 г.
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Математика», 3 семестр 2021– 2022 уч.г.
ВАРИАНТ 4
Задание №1
Даны две матрицы А =
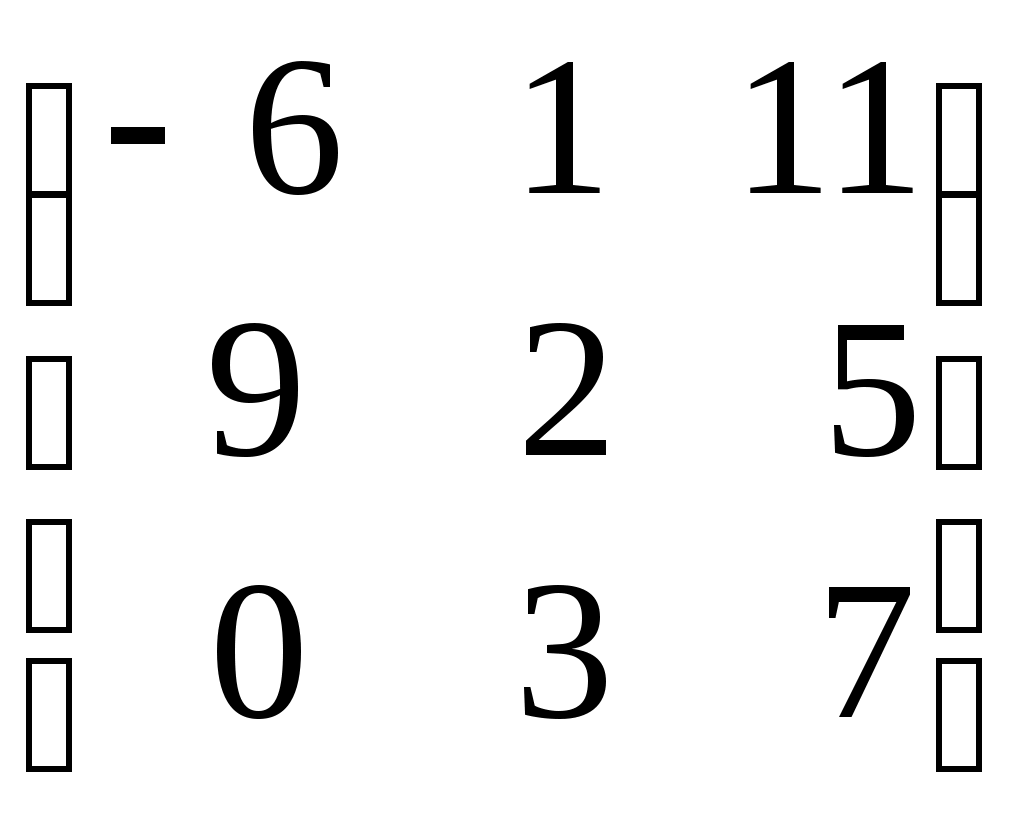и В = 
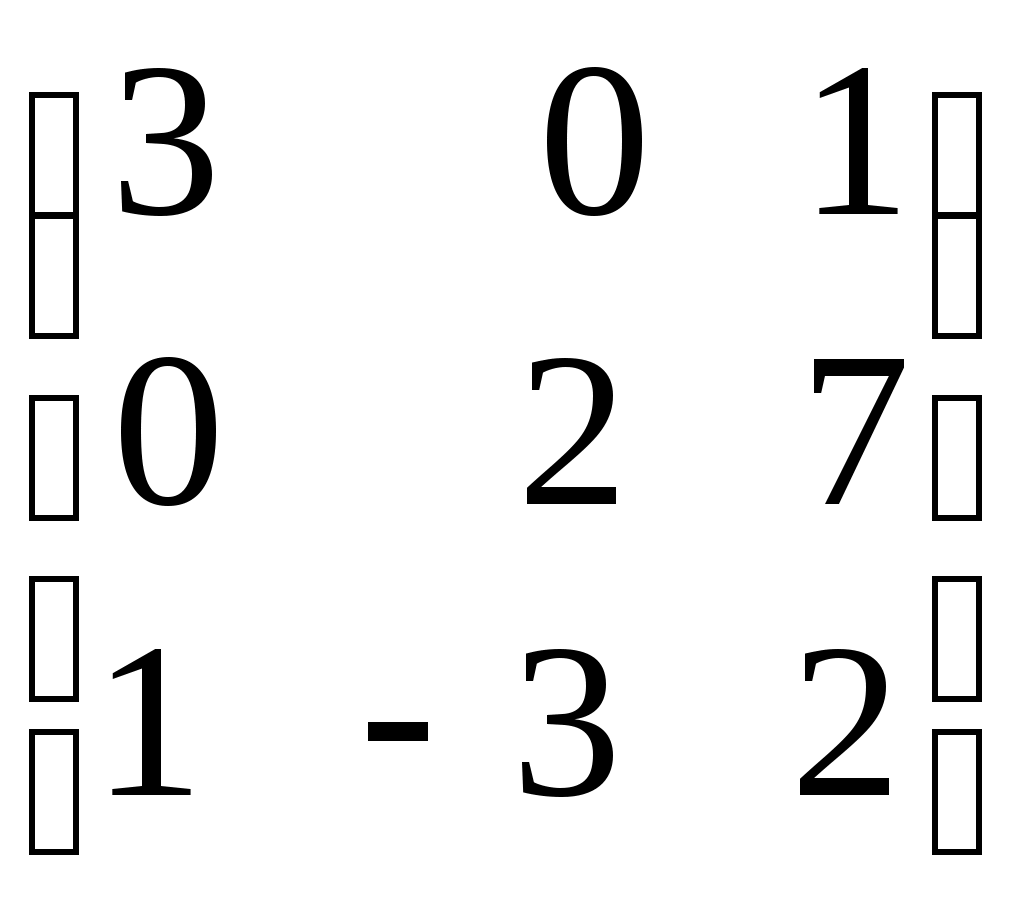. Найдите 1. А∙В; 2. В∙А; 3. 
; 4. определители матриц.Решение:
1. Определим А∙В.
А∙В =
∙ = 
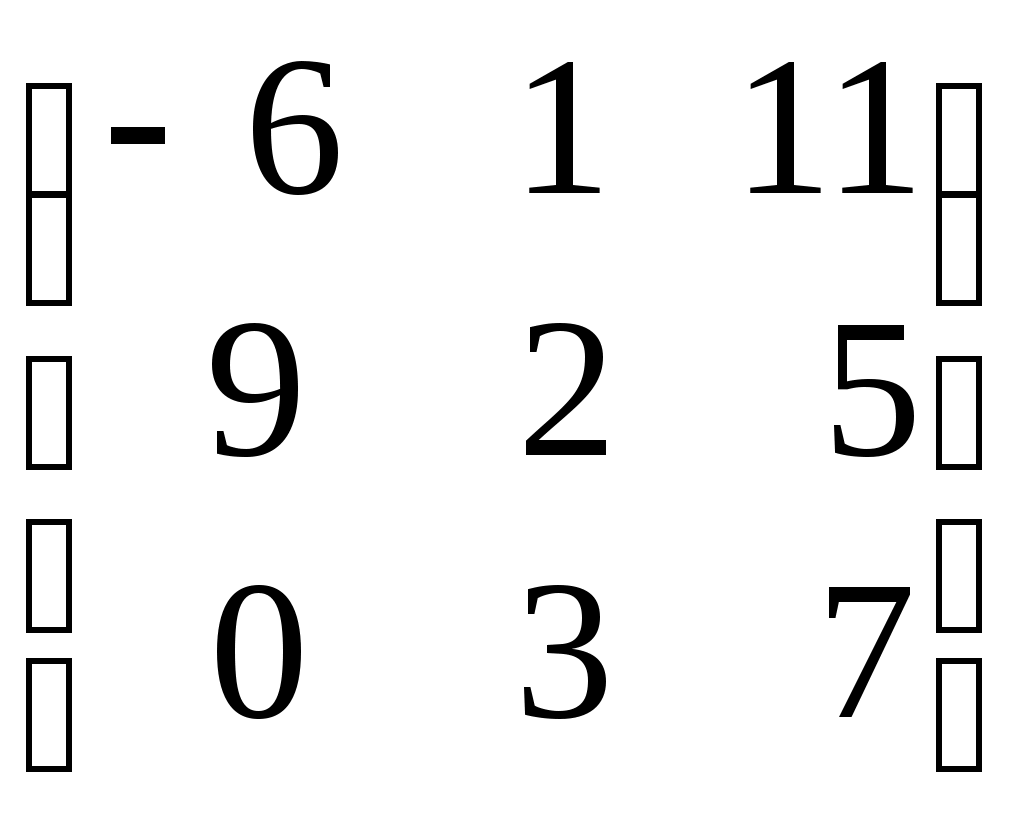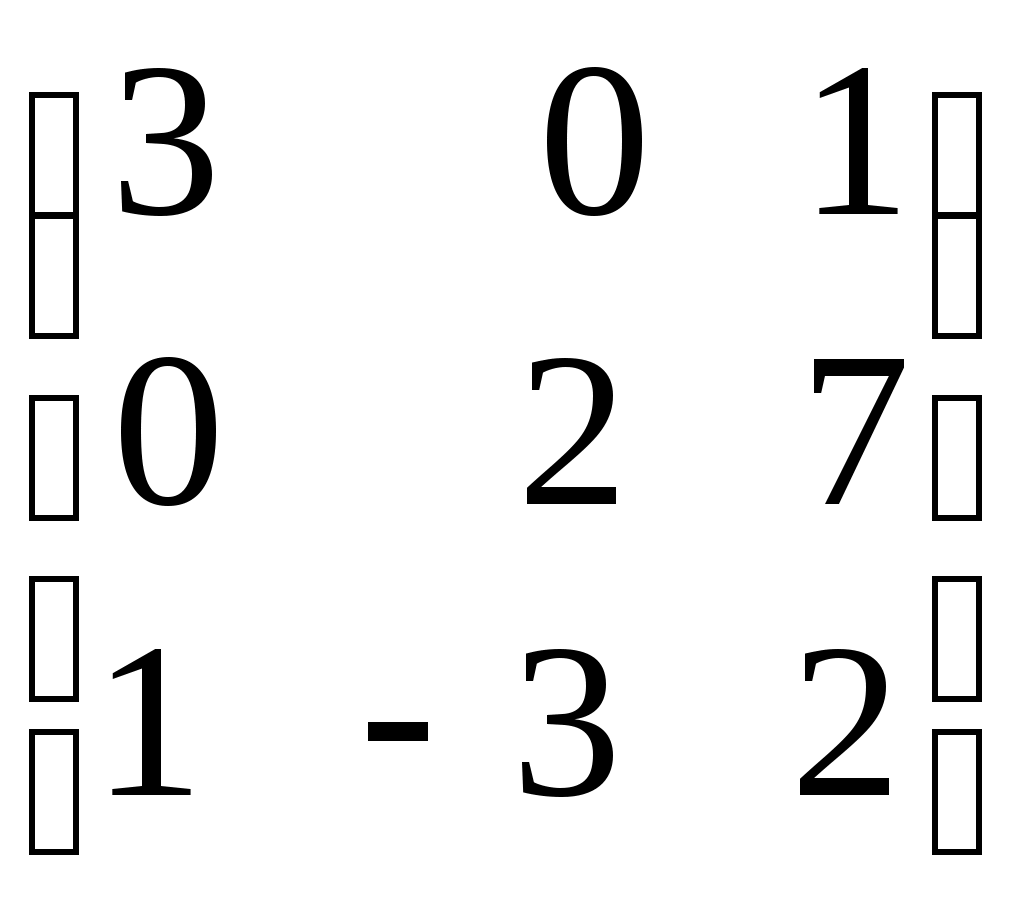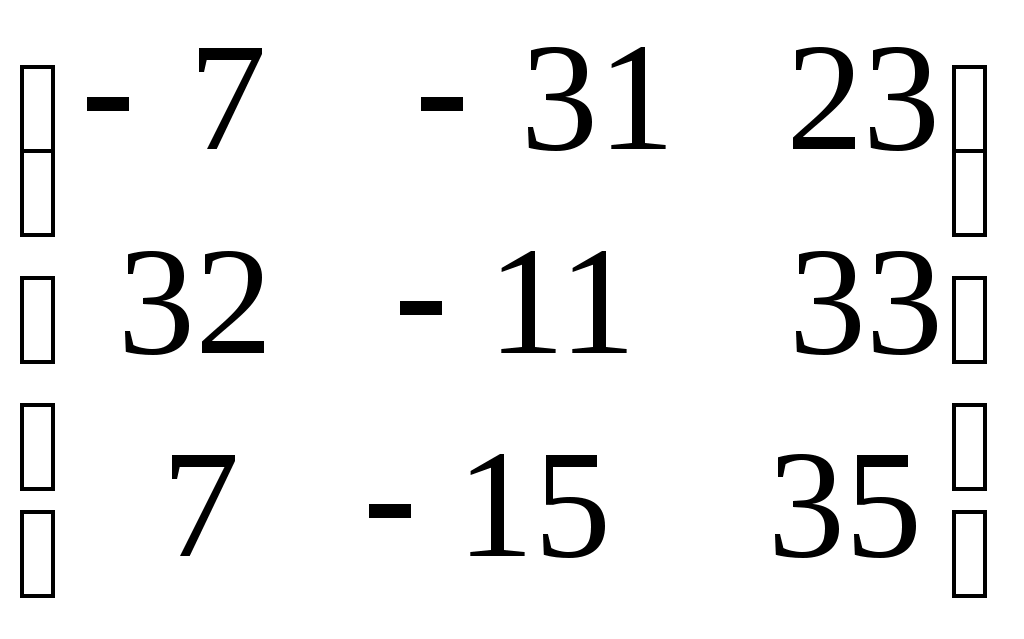
2. Определим В∙А.
В∙А =
∙ = 
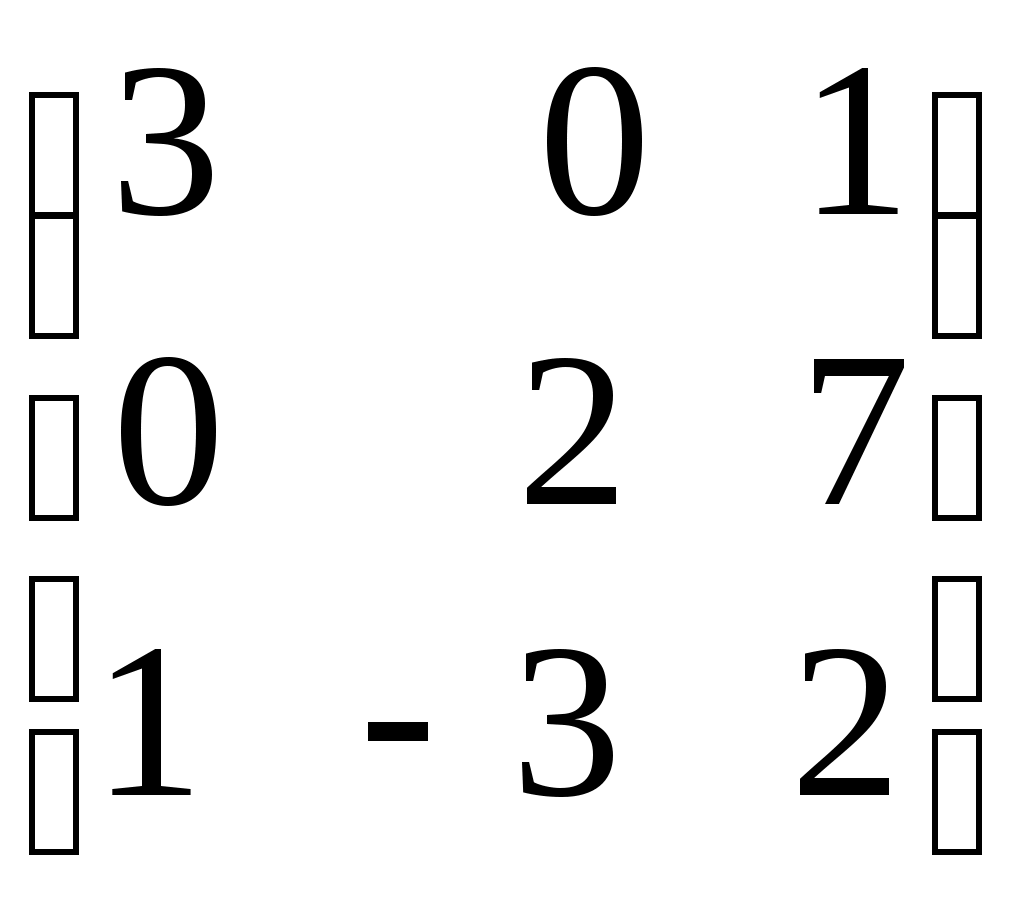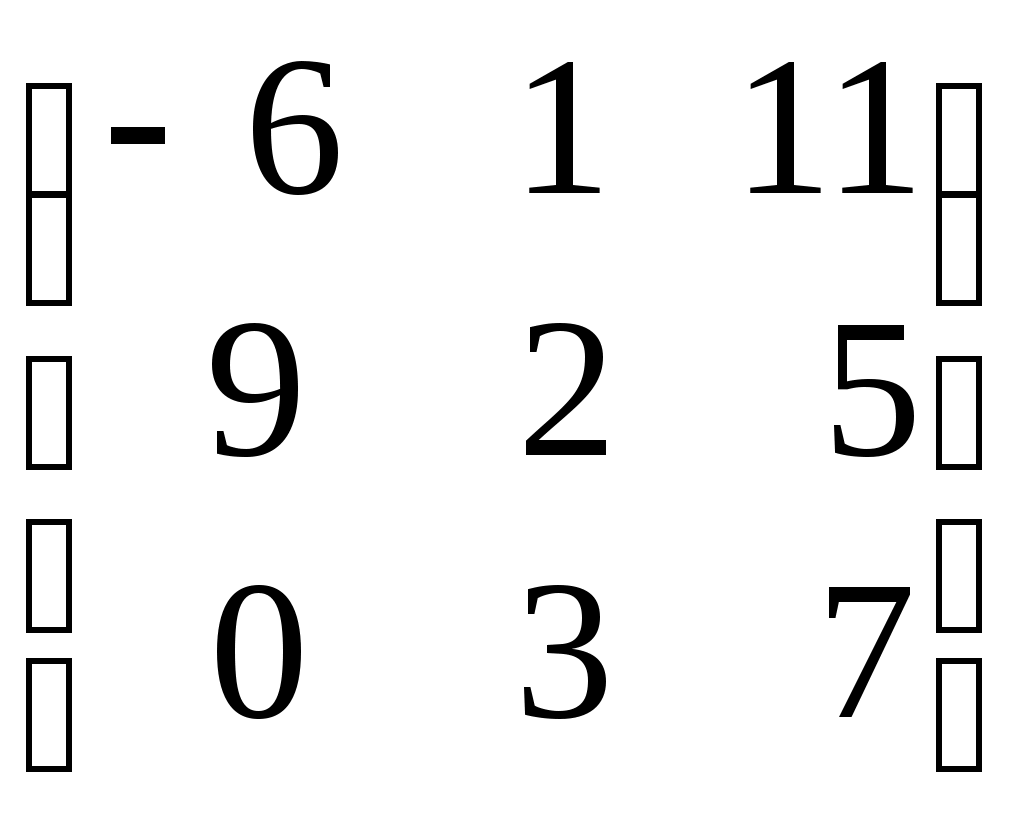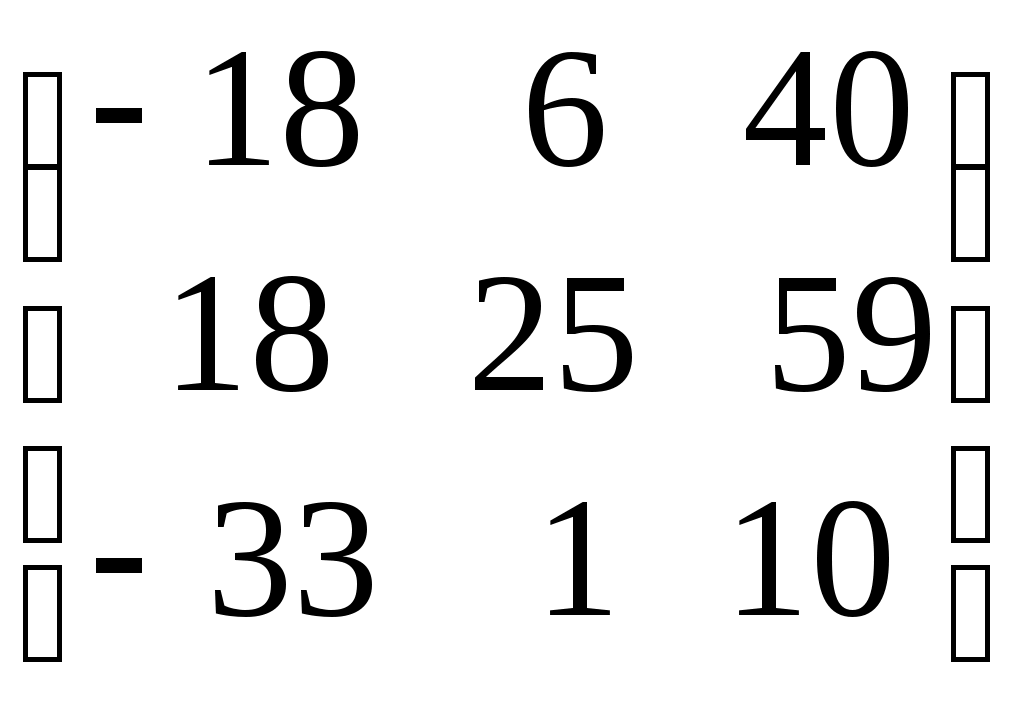
3. Определим
. = 
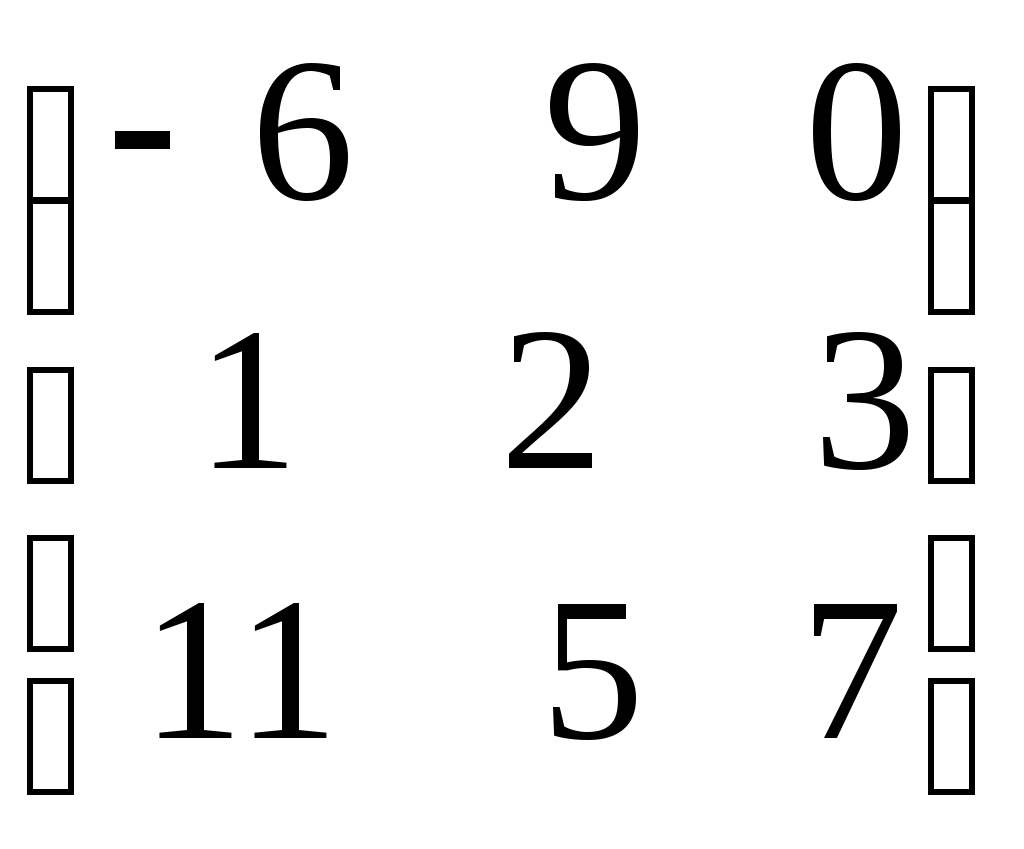
4. Определим│А│ и │В│.
│А│=
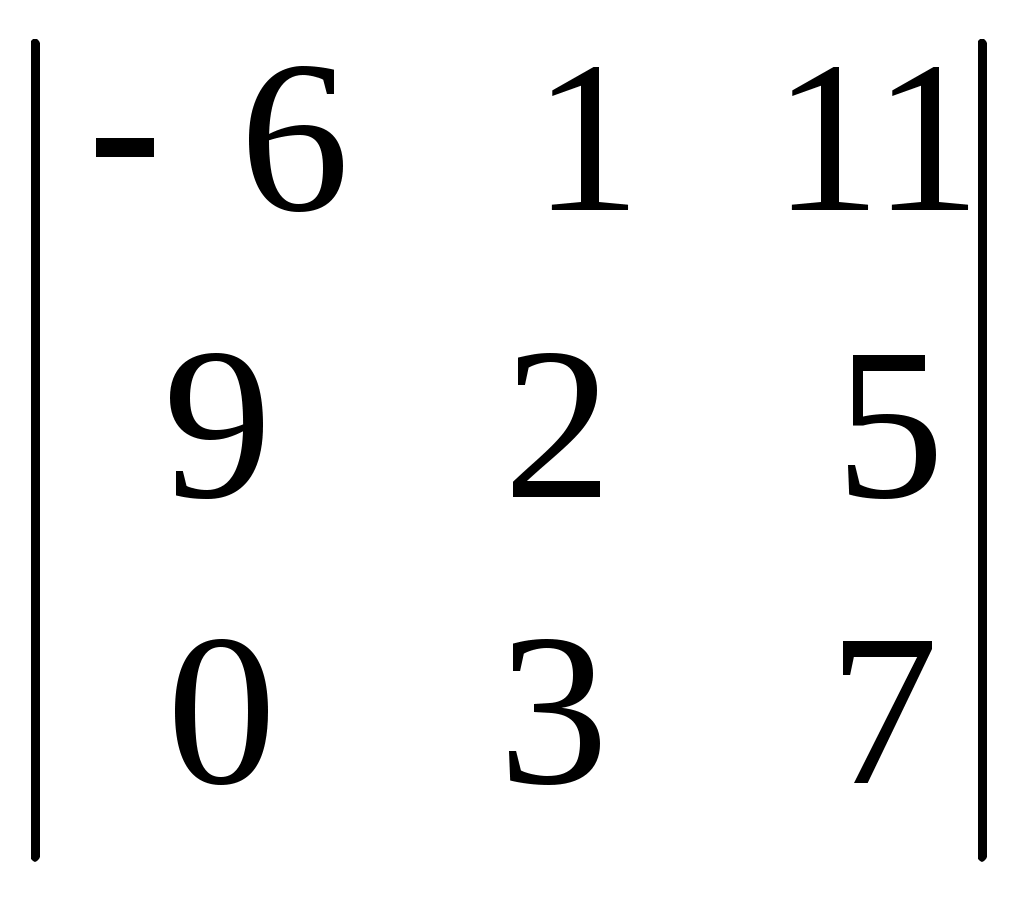= 297 – 84 + 90 – 63 = 240│В│=
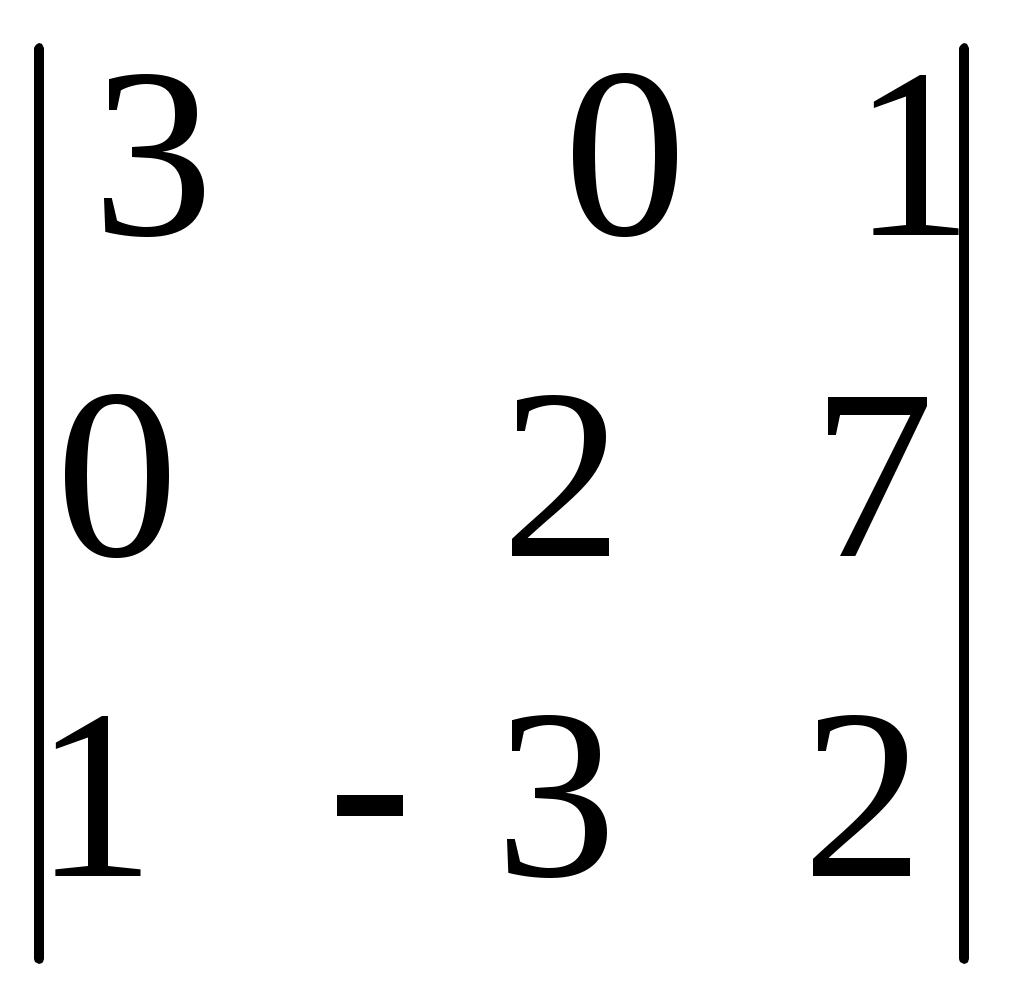= 12 – 2 + 63 = 73Ответ: 1. А∙В =
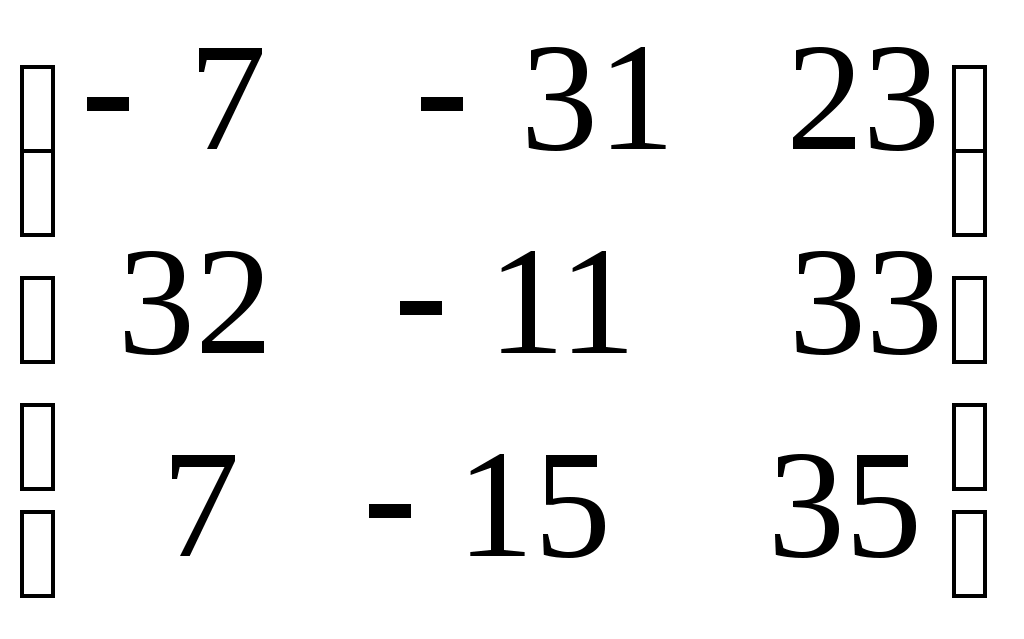; 2. В∙А = 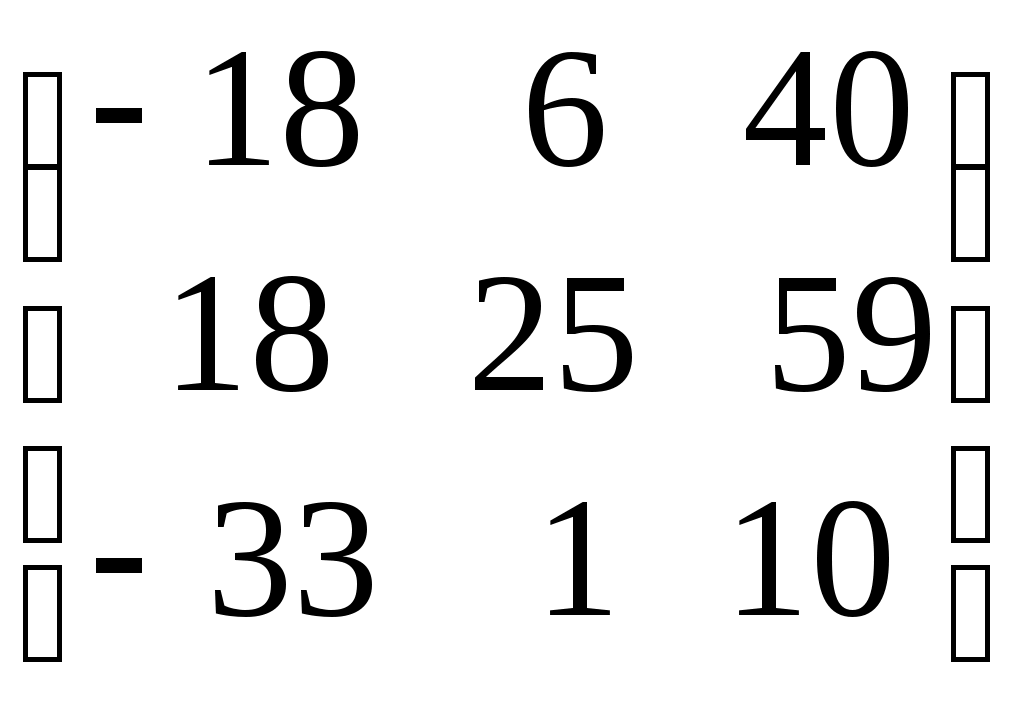; 3.
=
;4. │А│= 240; 5. │В│= 73.
Задание №2
Решите систему линейных уравнений по формулам Крамера.
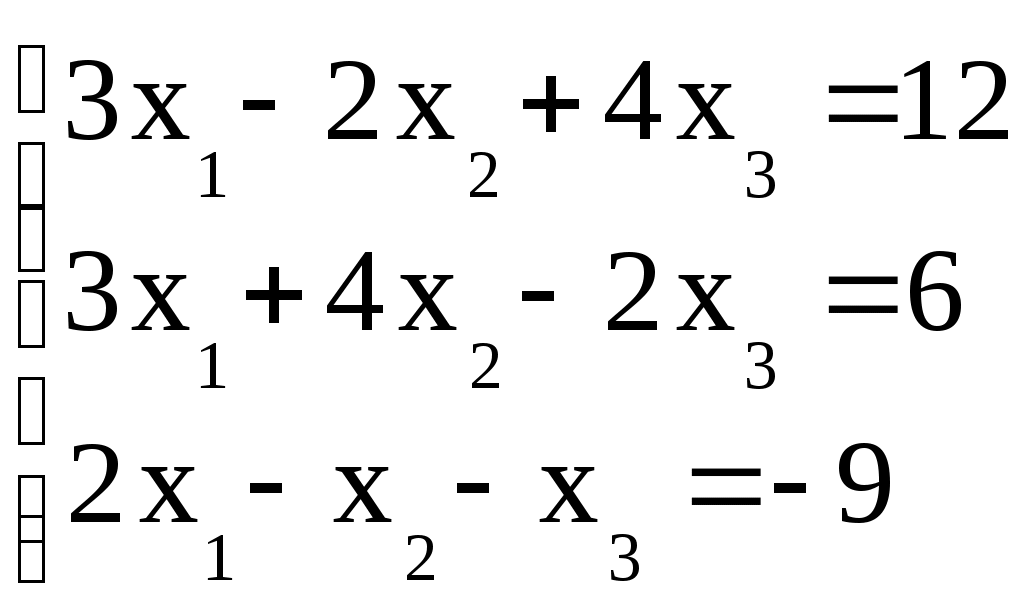
Решение:
Решим систему уравнений по формулам Крамера.
, 
, 
.│А│ =
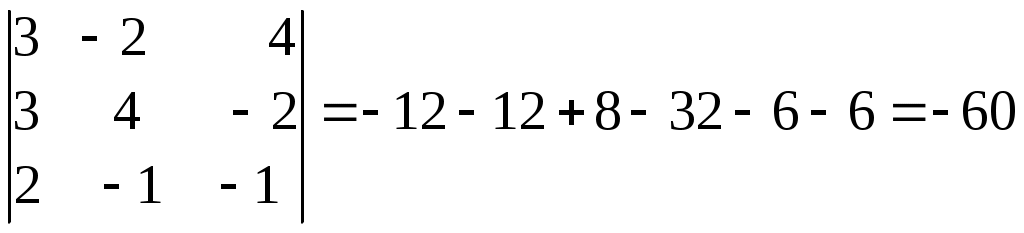≠ 0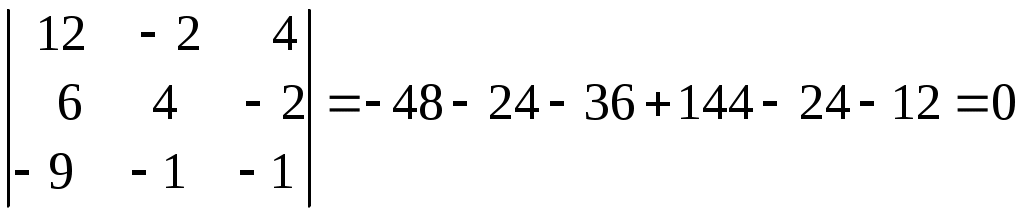
= 
= 
= 
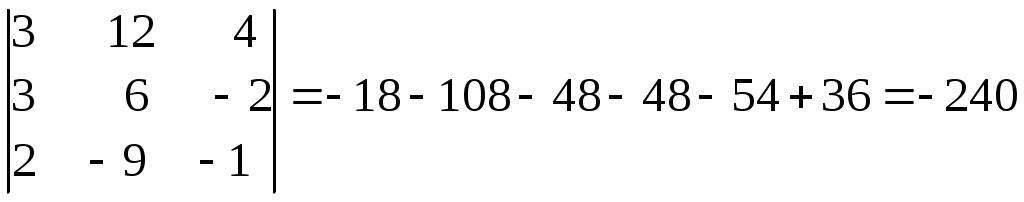
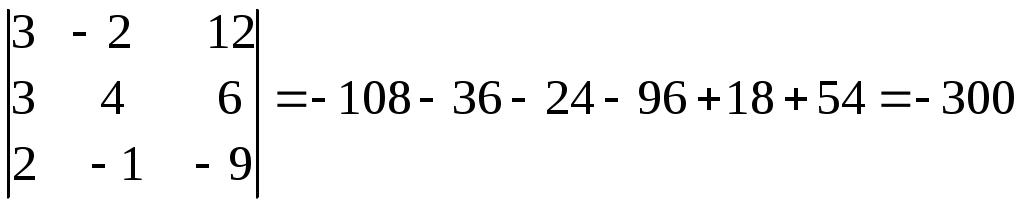
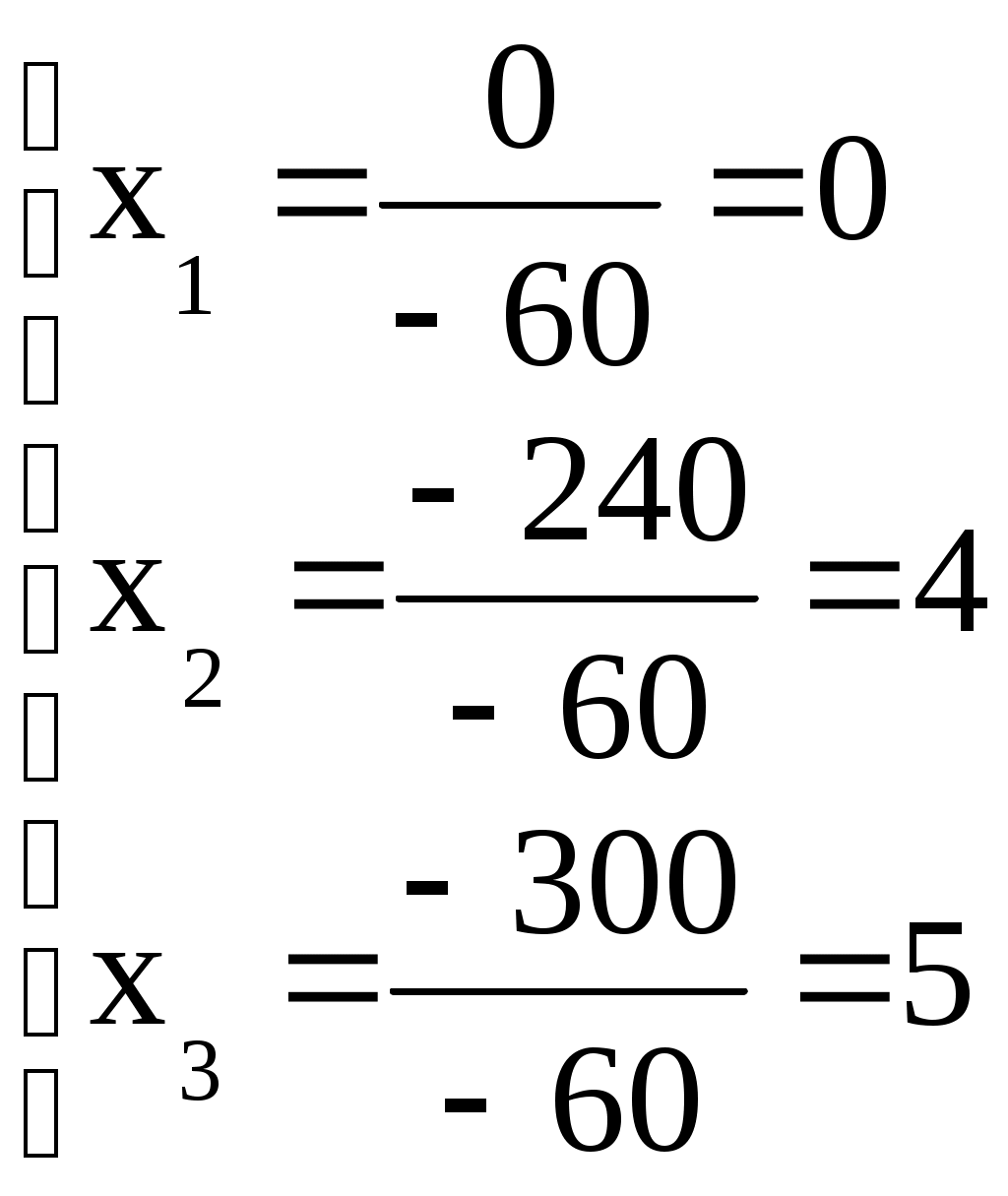
Проверка.
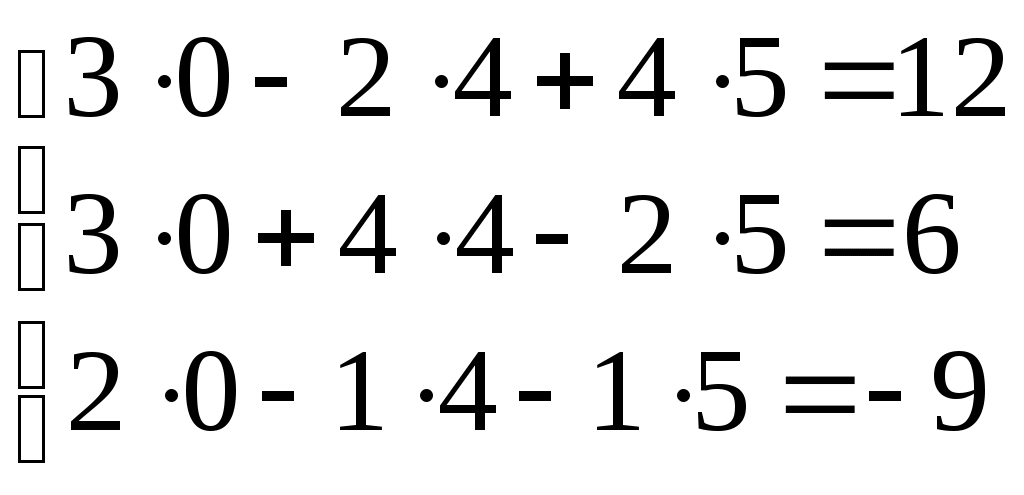
Ответ:
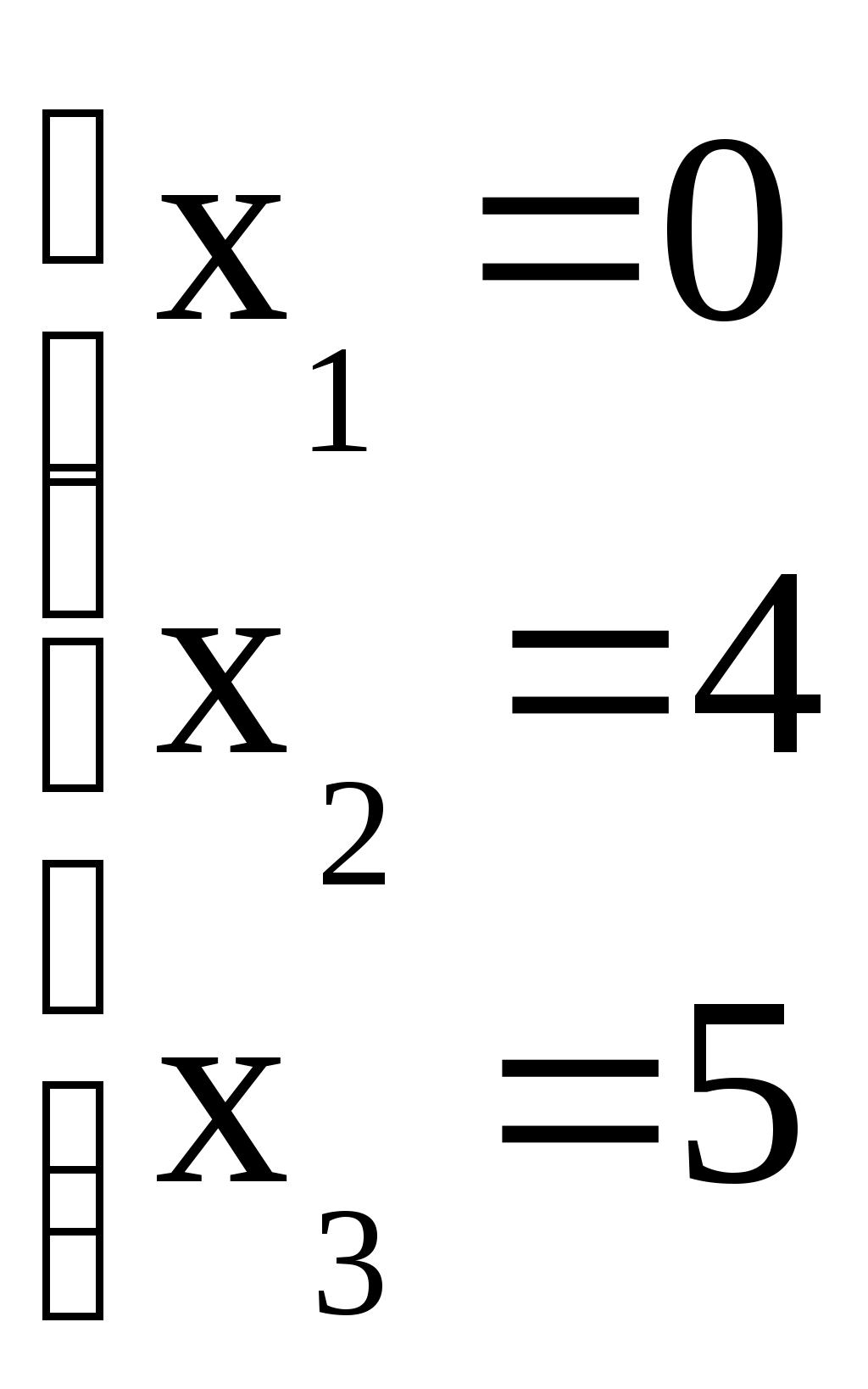
Задание №3
Решите матричное уравнение.
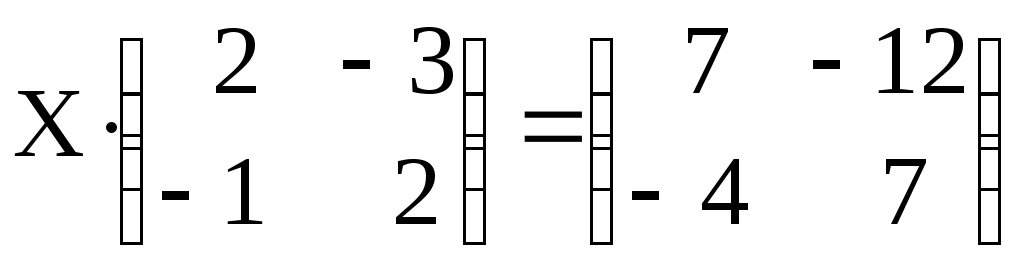
Решение:
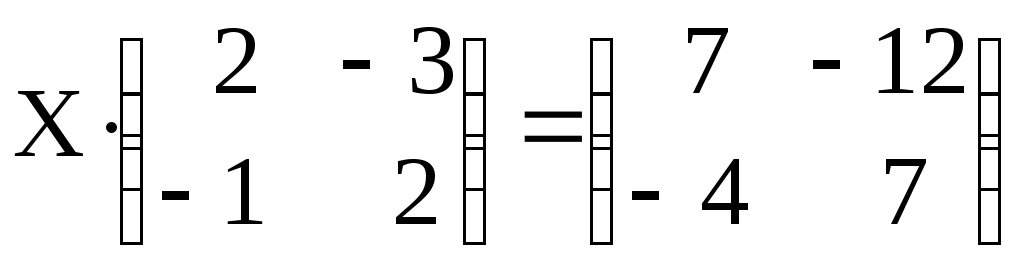
Х∙А = В → Х = В∙
, где 
А =
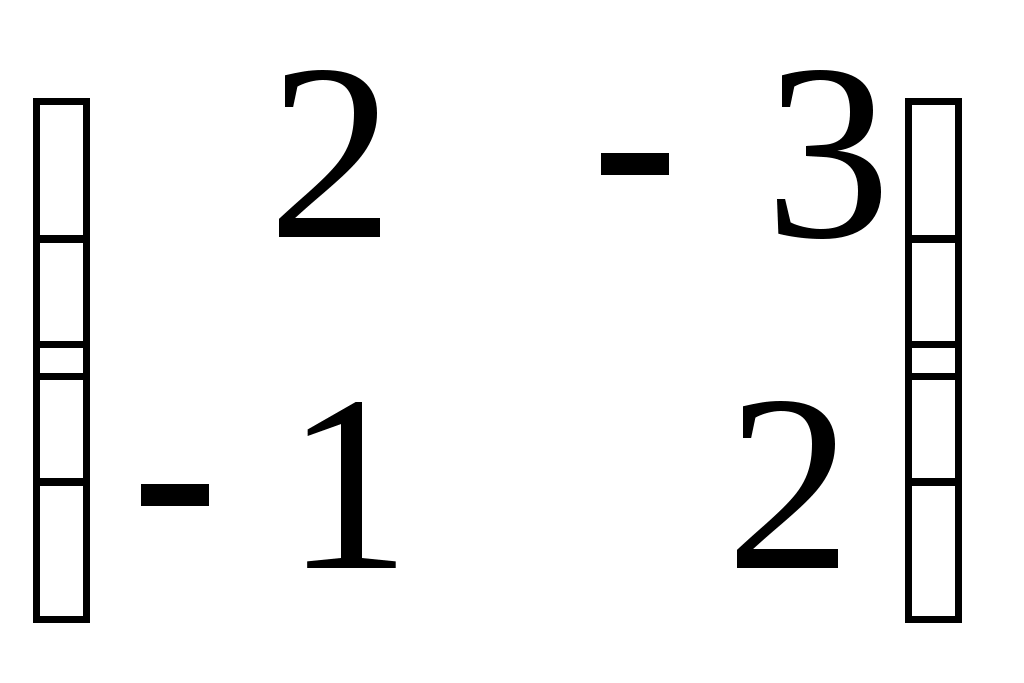, В =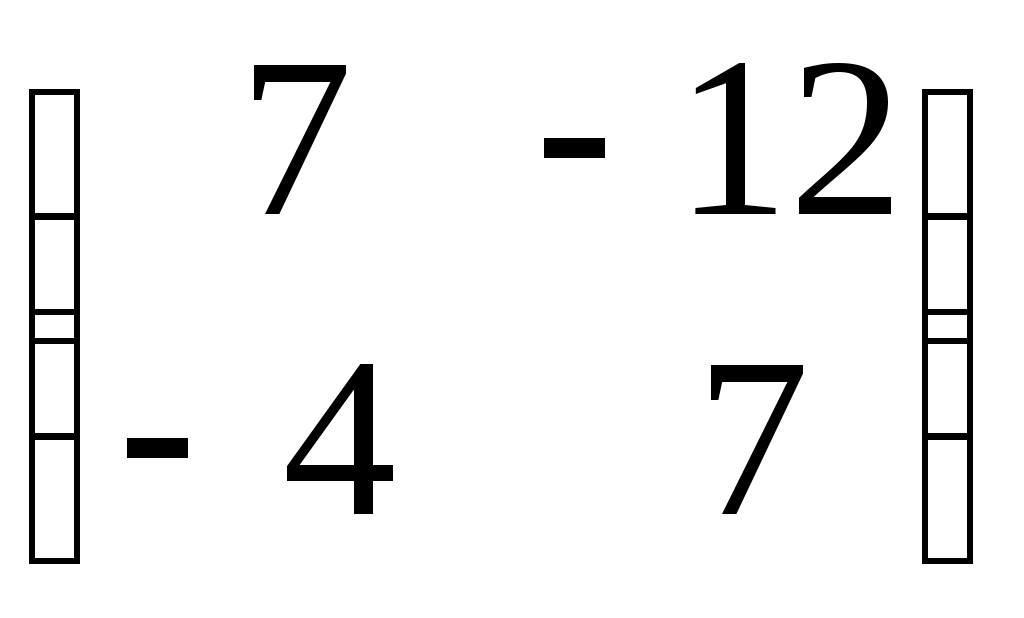 
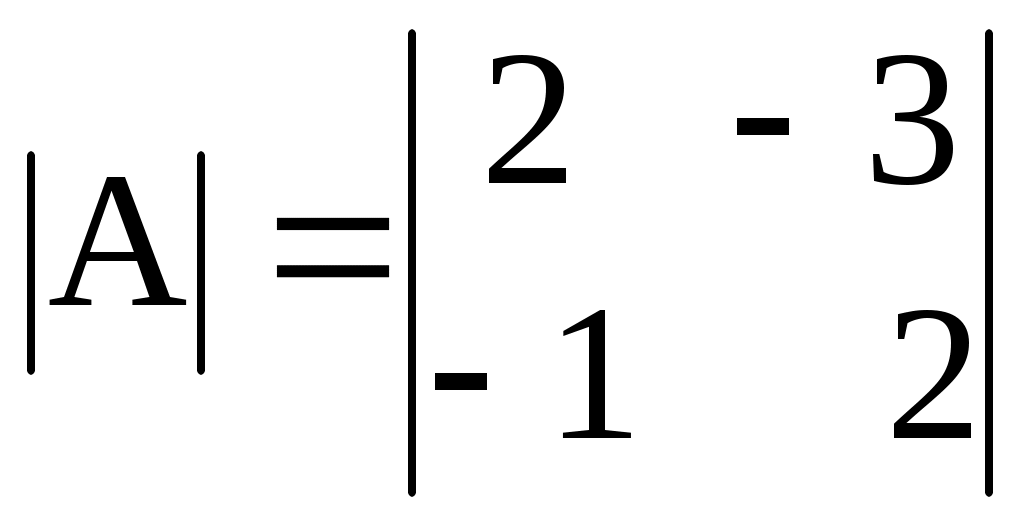= 4 – 3 = 1 ≠ 0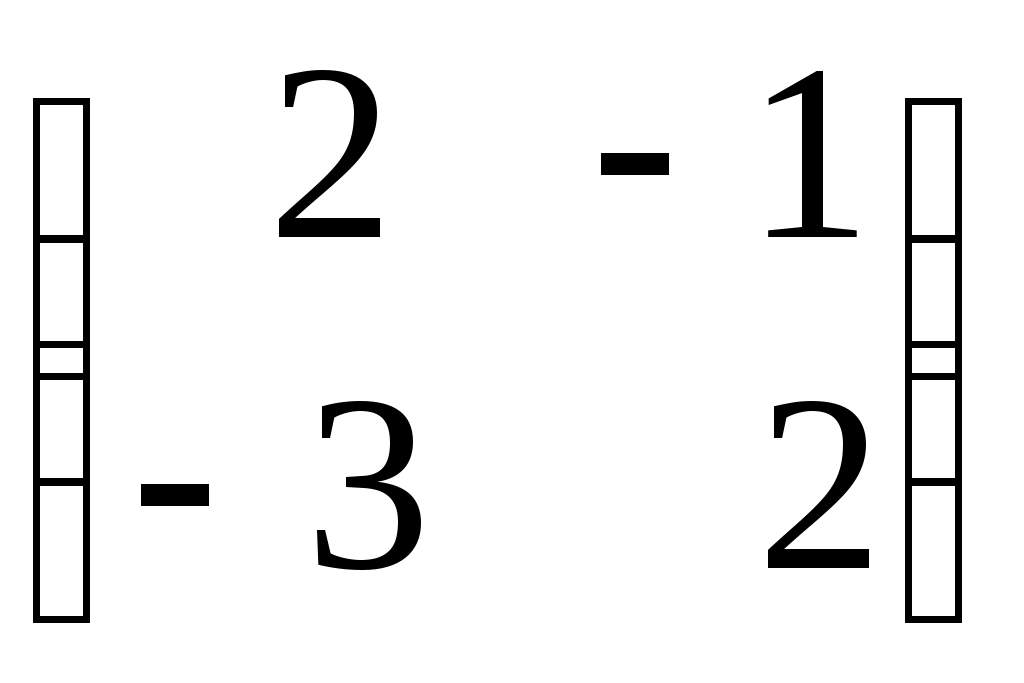
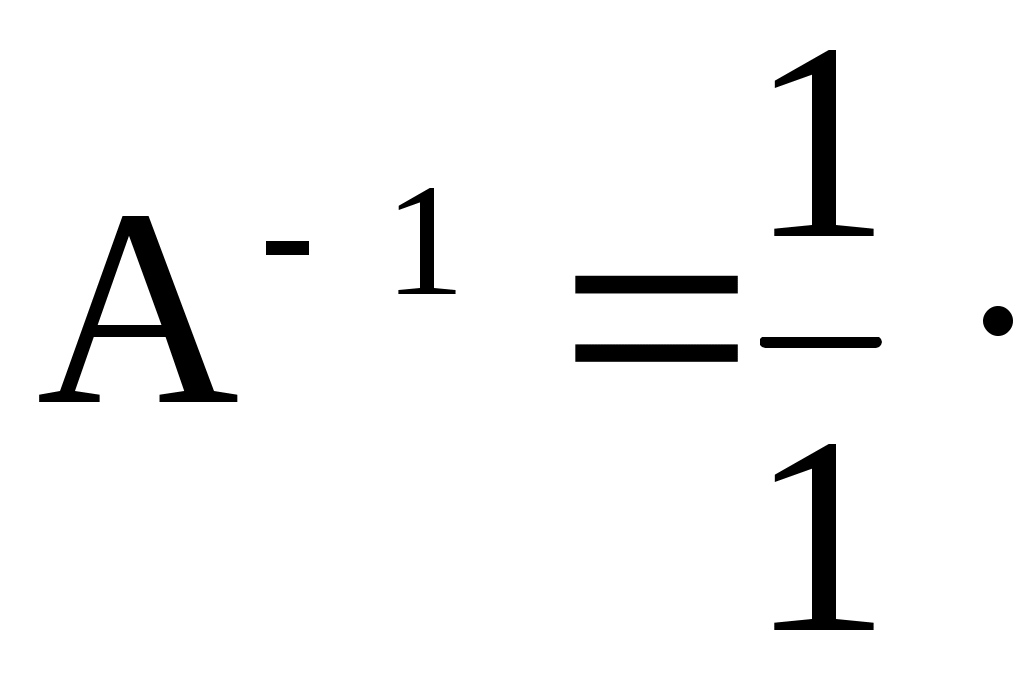
= Х =
∙ = 
Проверка.
Х∙А =
∙ = Ответ: Х =
.Задание №4
Найдите координаты, модуль и направляющие косинусы вектора
.А(2;2;3), В(3;2;4)
Решение:
1. Определим координаты вектора
.
= (3 – 2, 2 – 2, 4 – 3) = (1,0,1)2. Определим модуль вектора
.
3. Определим направляющие косинусы вектора
.
, 
, 
, 
, 
Ответ: 1.
= (1,0,1); 2. 
; 3. 
, 
, 
.Задание №5
Даны вершины A(–2;3), В(2;1), С(4; –2) треугольника ∆АВС. Выполнить чертёж. Найдите: а) уравнение стороны АВ. б) уравнение высоты СН. в) уравнение медианы АМ. г) расстояние от точки С до прямой АВ.
Решение:
а) Определим уравнение стороны АВ.
→ 
(АВ): х + 2у – 4 = 0 или
, 
б) Определим уравнение высоты СН.
у –
= 
∙(х – 
)Так как СН перпендикулярна АВ, то
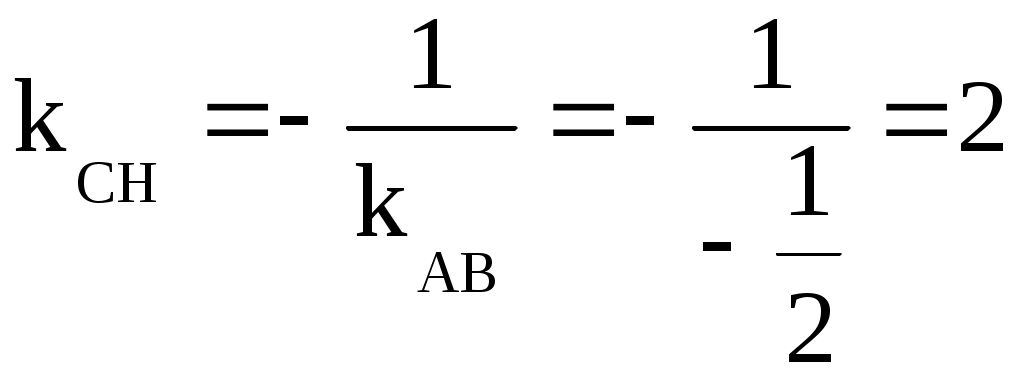
у + 2 = 2∙(х – 4)
(СН): 2х – у – 10 = 0 или
в) Определим уравнение медианы АМ.
Определим координаты точки М – середины стороны ВС.
Имеем координаты точки М
.
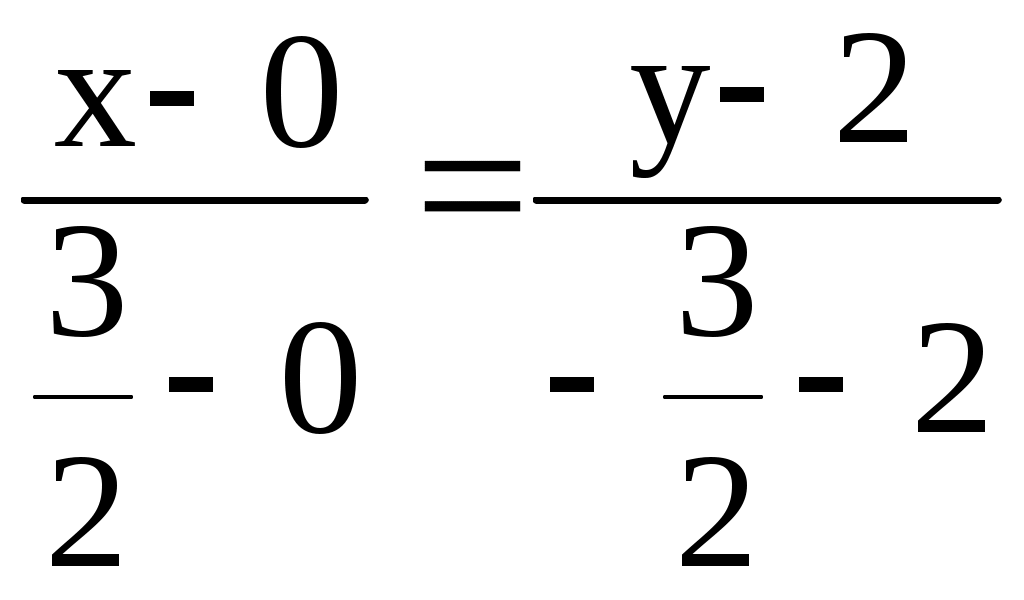
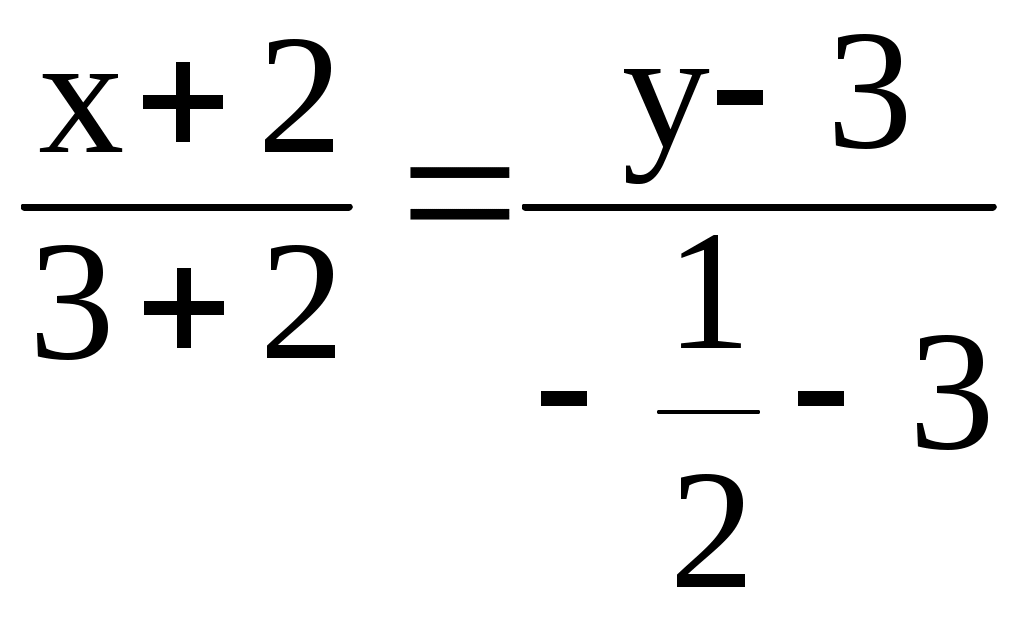
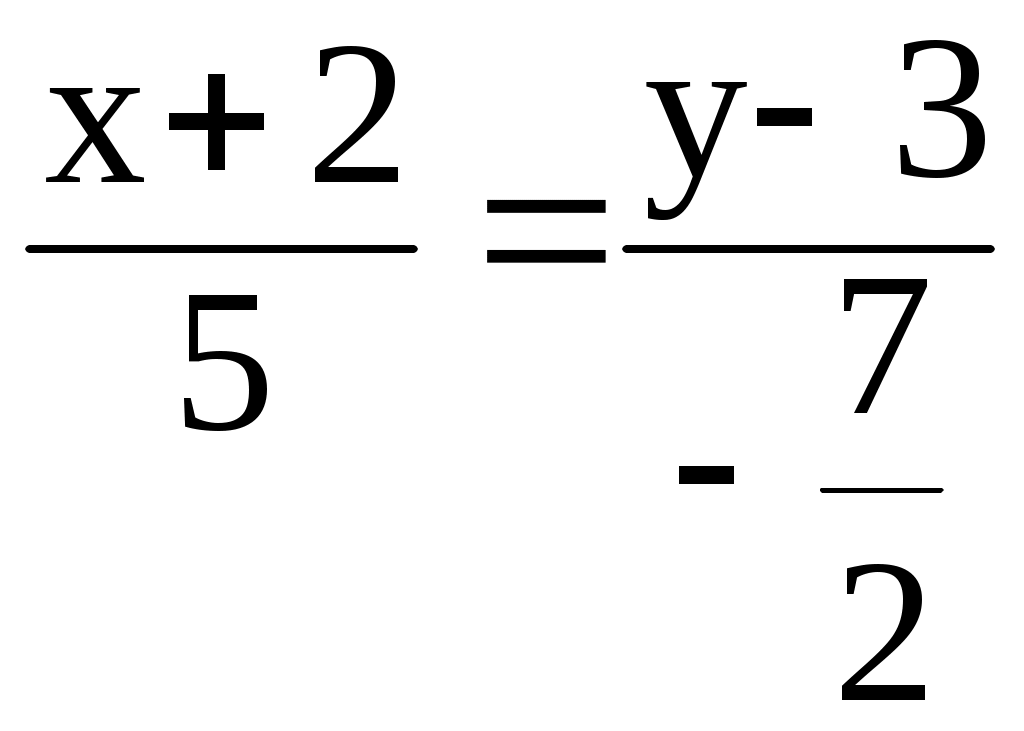
–7(х + 2) = 10(у – 3)
(АМ): 7х + 10у – 16 = 0 или у =
г) Определим расстояние от точки С до прямой АВ.
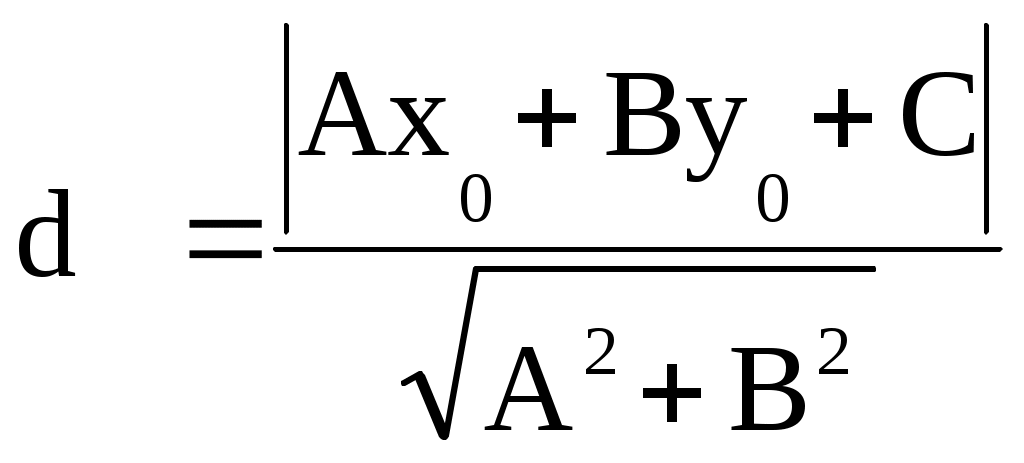
(ед.)Сделаем чертеж (рис. 7).
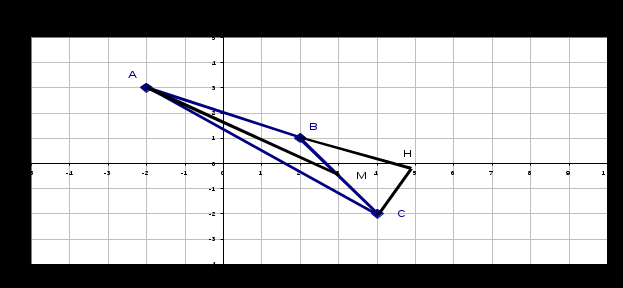
Ответ: а) (АВ): х + 2у – 4 = 0; б) (СН): 2х – у – 10 = 0;
в) (АМ): 7х + 10у – 16 = 0; г)
(ед.).Задание №6
Даны четыре точки
(3;2;–1), 
(–2;1;2), 
(–2;2;1), 
(0;–1;–2) Составьте уравнения: а) плоскости ; б) прямой ; в) прямой М, перпендикулярной плоскости; г) прямой N, проходящей через точку , параллельно прямой . Решение:
а) Определим уравнение плоскости