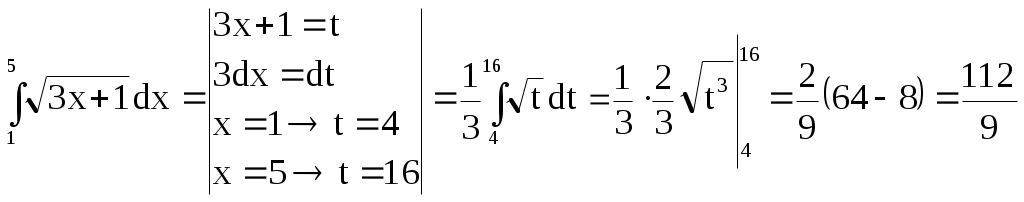Файл: Контрольная работа по дисциплине Математика, 3 семестр 2021 2022 уч г. Вариант 4 Задание 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
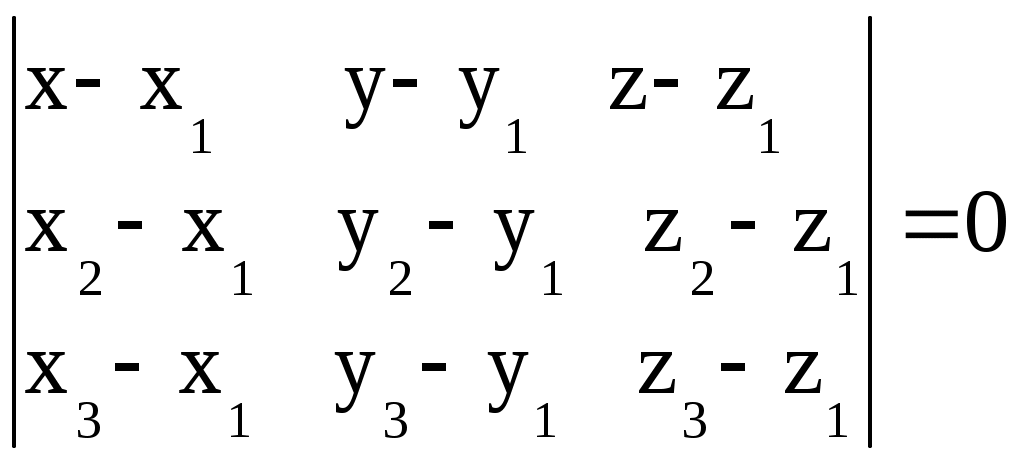
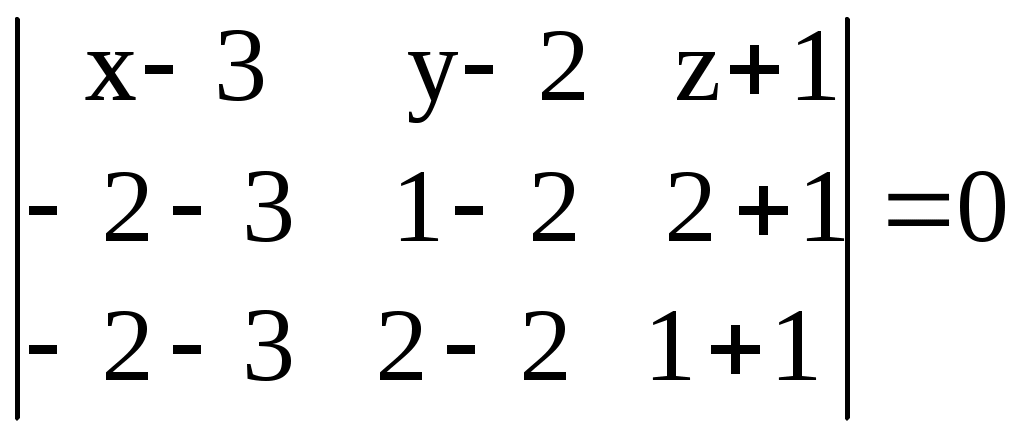
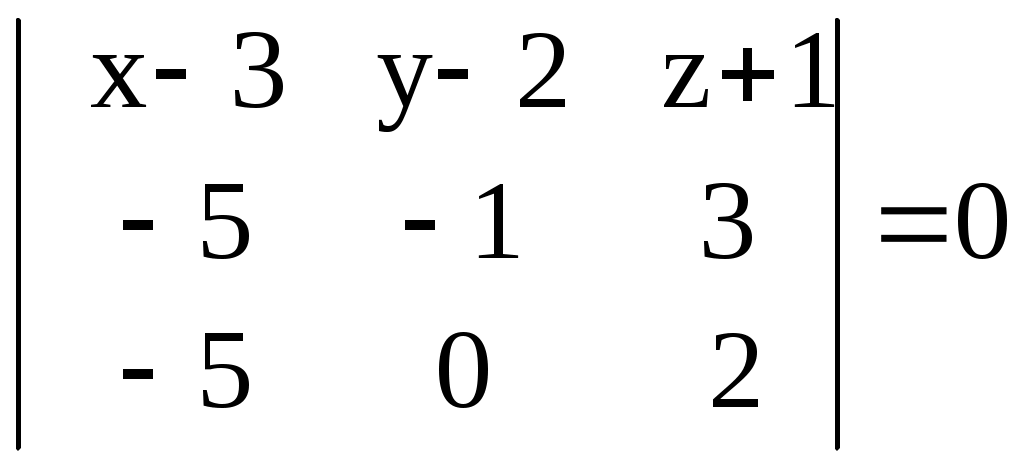
– 2(х – 3) – 15(y – 2) – 5(z + 1) +10(y – 2) = 0
2х + 5y + 5z – 11 = 0
б) Определим прямой
.
в) Определим уравнение прямой
М, перпендикулярной плоскости.Так как прямая и плоскость перпендикулярны, то нормальный вектор плоскости
= (2,5,5) будет являться направляющим вектором искомой высоты. 
искомое уравнение высотыг) Определим уравнение прямой
N, проходящей через точку , параллельно прямой . Так как прямые параллельны, то направляющий вектор прямой
= (–5, –1,3) равен направляющему вектору прямой N.
искомое уравнение прямой
Ответ: а) 2х + 5y + 5z – 11 = 0; б)
; в) 
;г)
.Задание №7
Вычислите пределы функций
1)
; 2) 
Решение:
1)
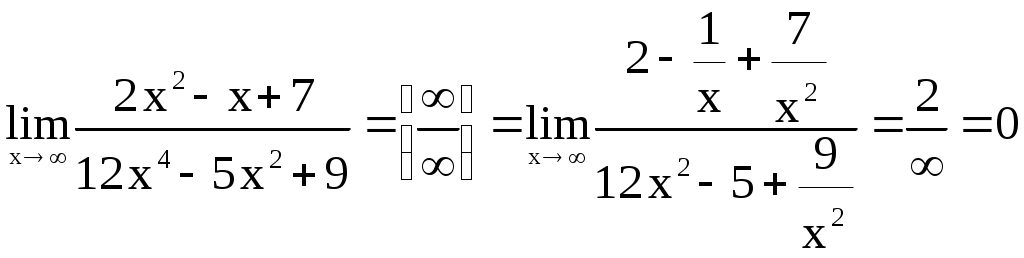
2)
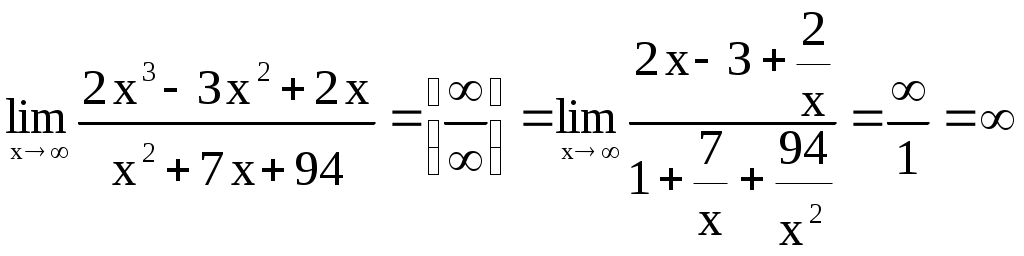
Ответ: 1) 0; 2)
.Задание №8
Найдите производную функции.
Решение:
– – 
+ 2∙(6x – 3)∙6 = 
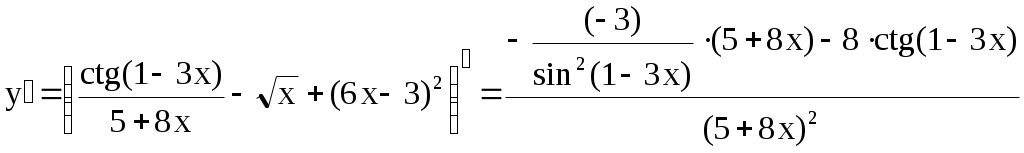– + + 12(6x – 3) =
– + 72x – 36 ==
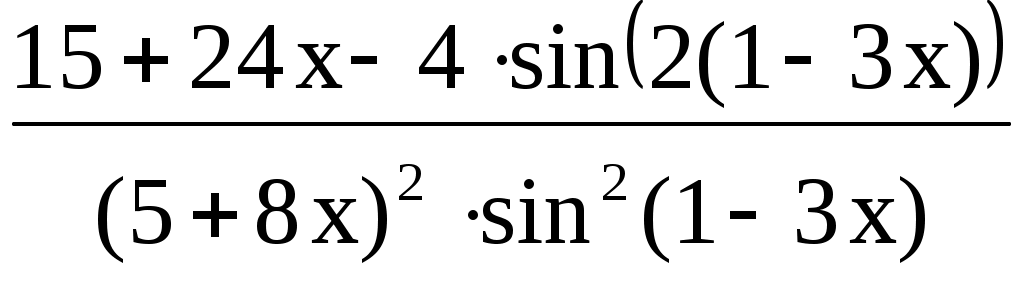– + 72x – 36Ответ:
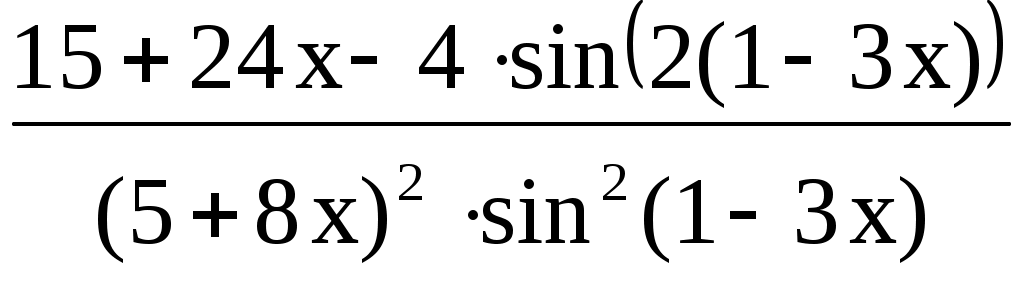– + 72x – 36.Задание №9
Исследуйте функцию на монотонность. Исследуйте функцию на экстремум. Найдите интервалы выпуклости и точки перегиба функции.
Решение:
1. Исследуем функцию на монотонность.
Определим
(x).
(x) =
(x) = 0 при 
= 0 x = 0,
| x |  |  |  | 0 |  |  |  |
| (x) | – | 0 | + | 0 | – | 0 | + |
| y(x) | убывает | min | возрастает | max | убывает | min | возрастает |
2. Определим экстремумы функции,
3. Найдем интервалы выпуклости и точки перегиба.
Определим
(x).
(x) = 
(x) = 0 при 
= 0
| x |  |  |  |  |  |
 (x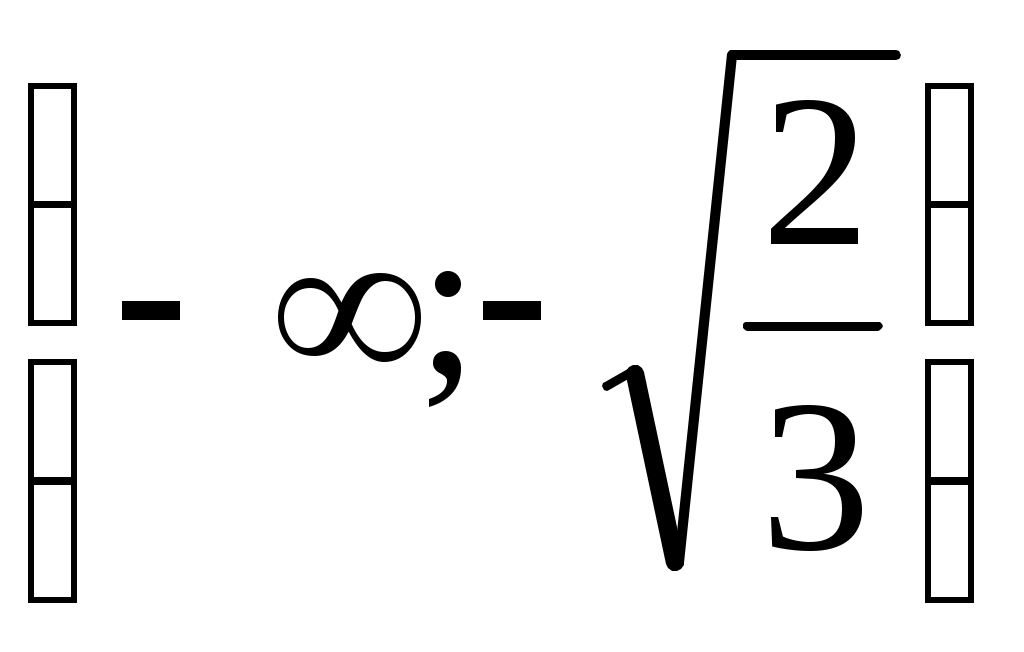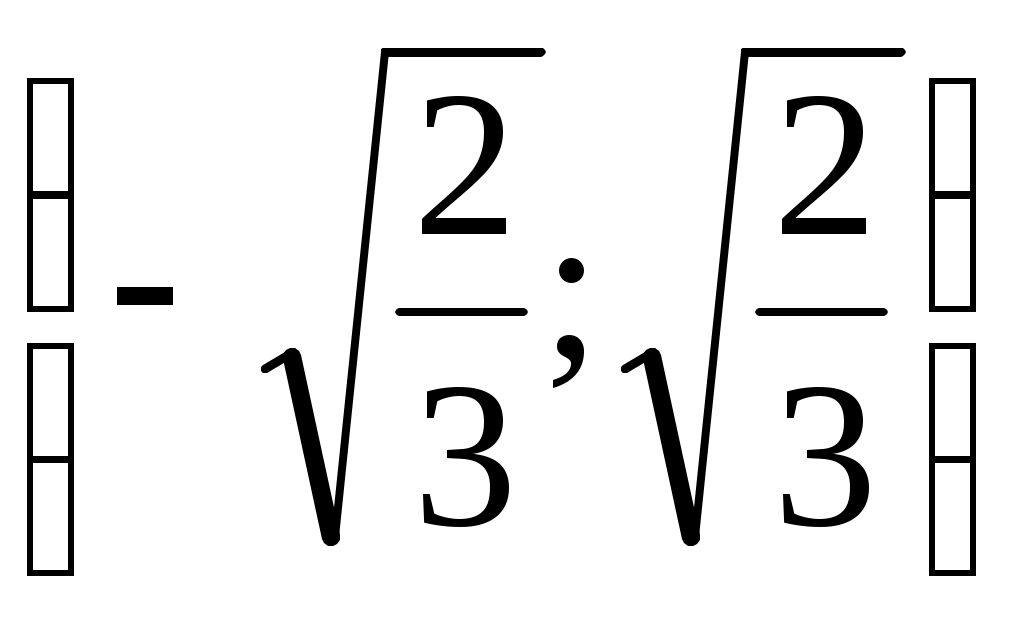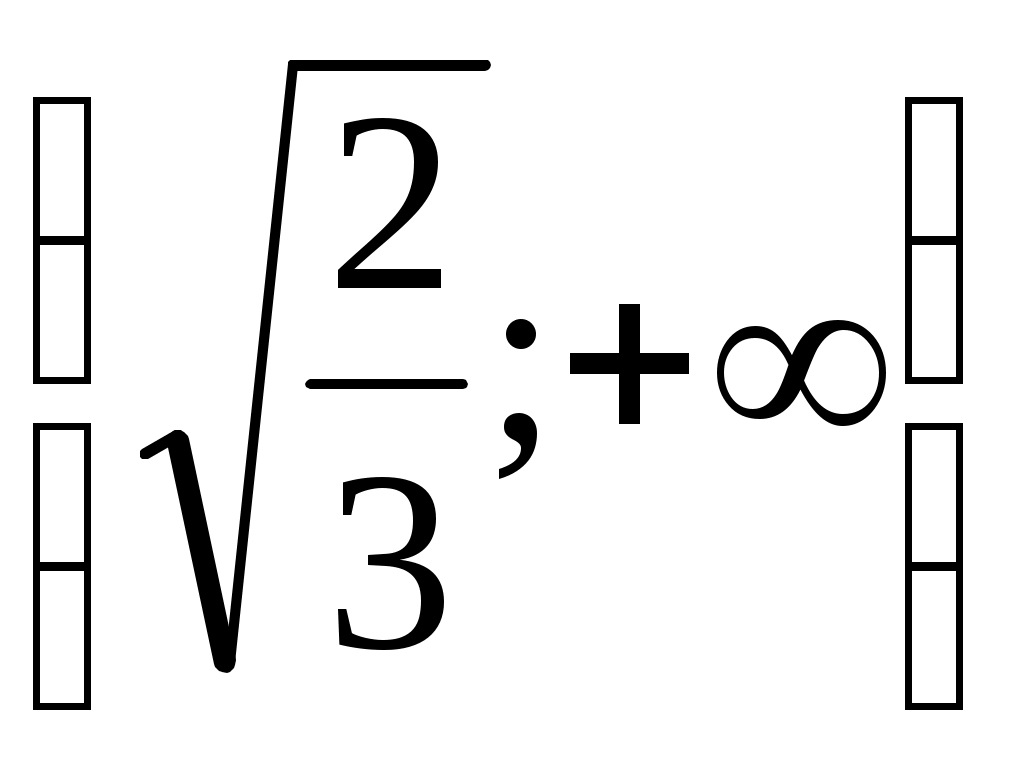) | + | 0 | – | 0 | + |
| y(x) | вогнутая | точка перегиба | выпуклая | точка перегиба | вогнутая |
Точки перегиба:
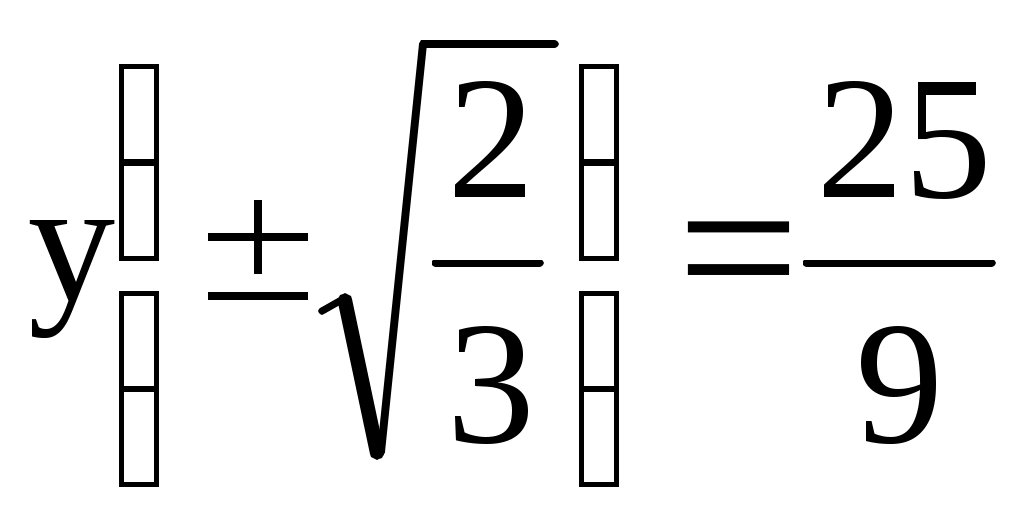
4. Сделаем чертеж (рис. 10).
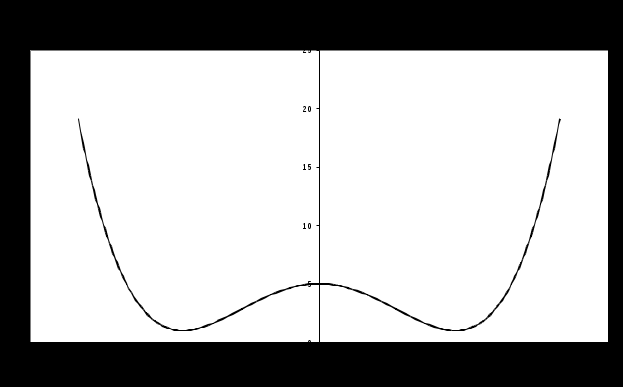
Ответ: 1.
, 
, 
;2. Точки перегиба:
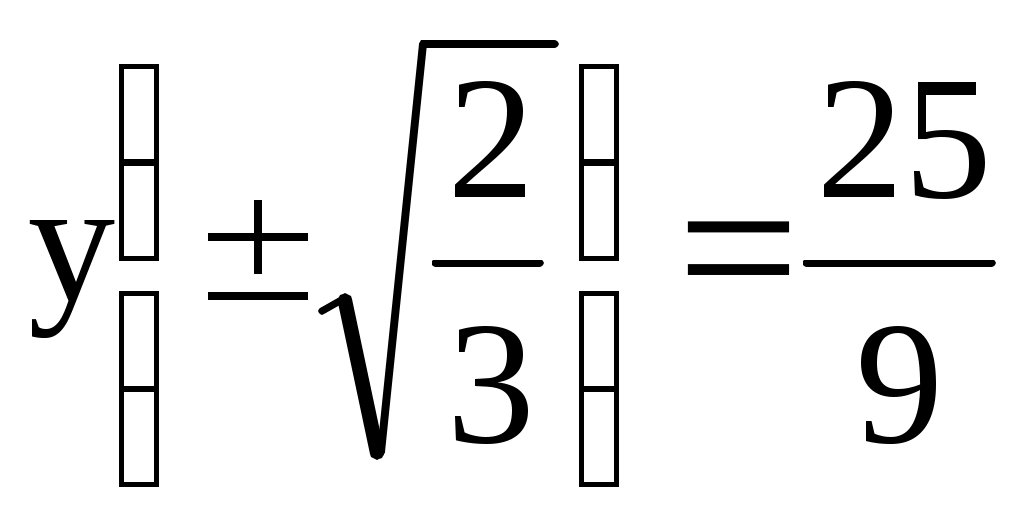.Задание №10
Найдите наименьшее и наибольшее значение функции на отрезке.
Решение:
Определим
(x). (x) = 
(x) = 0 при 
= 0 
(x) не существует при 
= 0 
= –5 – наименьшее значение. 
= –1 – наибольшее значение. 
= –3 Ответ:
; 
.Задание №11
Используя метод интегрирования по частям, вычислите интеграл.
Решение:
=
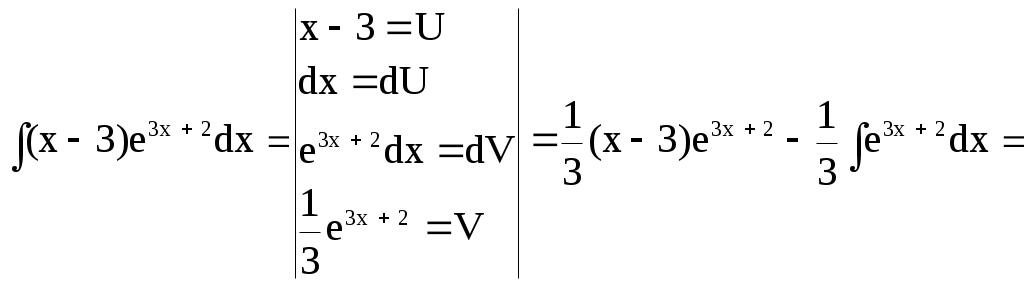
Ответ:
.Задание №12
Методом замены переменной вычислите интеграл.
Решение:
+
=
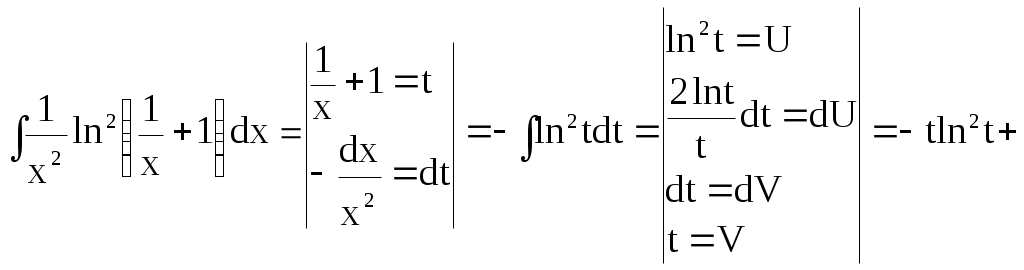
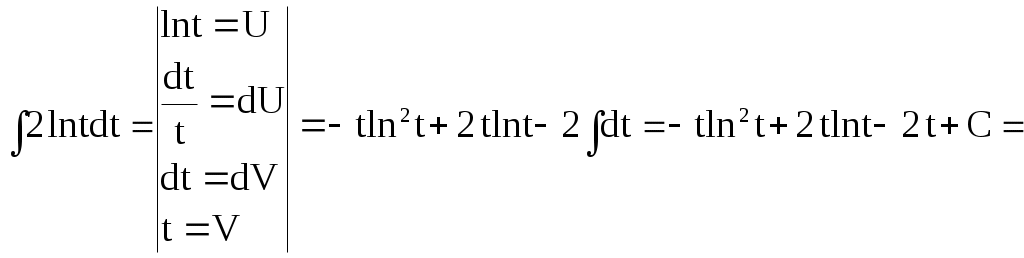
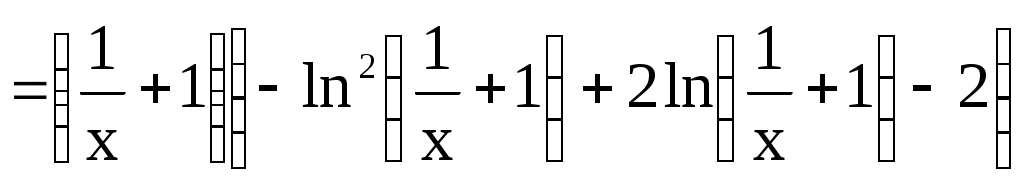
Ответ:
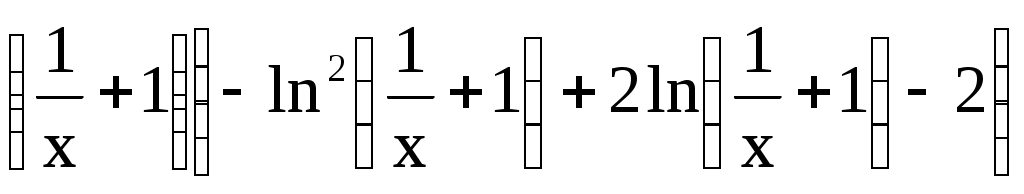.Задание №13
Вычислите интеграл
по формуле Ньютона – Лейбница.Решение:
