Файл: Связи и информатики.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Курсовая работа

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 39

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования

_______________________________________________

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

Кафедра общей теории связи

Курсовая работа по дисциплине ОТС

(Основы теории связи)

Вариант №10

Выполнил: **********

студ. гр. ******

Проверил: Сухоруков А.С.

Москва ****
Оглавлени

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ 1

Кафедра общей теории связи 1

Техническое задание 3

1. Техническое задание 3

2. Исходные данные 6

2. Структурная схема системы электросвязи 7

3. Выполнение задания 8

4. Временные диаграммы 23

5. Список использованной литературы 25


Техническое задание


Непрерывное сообщение А(t), наблюдаемое на выходе источника сообщений (ИС), представляет собой реализацию стационарного гауссовского случайного процесса с нулевым средним и известной функцией корреляции 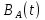. Данное сообщение передается в цифровом виде в системе электросвязи, изображённой на Рис. 1.

В ПДУ системе не основе АЦП сообщение преобразуется в первичный цифровой сигнал ИКМ, который модулирует один из информационных параметров высокочастотного гармонического переносчика. В результате формируется канальный сигнал 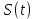ДАМ, ДЧМ или ДОФМ.

Сигнал дискретной модуляции передается по узкополосному гауссовскому НКС, в котором действует аддитивная помеха .

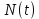В ПРУ системы принятая смесь сигнала и помехи 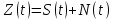подвергается при детектировании либо КП, либо НП с последующим поэлементным принятием решения методом однократного отсчета. Прием сигналов ДОФМ осуществляется либо методом СФ, либо методом СП.


Восстановление (оценка) переданного сообщения по принятому с искажениями сигналу ИКМ осуществляется на основе ЦАП с последующей ФНЧ.

В курсовой работе требуется выполнить следующее:

  1. Изобразить структурную схему системы электросвязи и пояснить назначение ее отдельных элементов.

  2. По заданной функции корреляции исходного сообщения:

    1. рассчитать интервал корреляции, спектр плотности мощности и начальную энергетическую ширину спектра сообщения;

    2. построить в масштабе графики функции корреляции и спектра плотности мощности; отметить на них найденные в п. а) параметры.

  3. Считая, что исходное сообщение воздействует на ИФНЧ с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения:

    1. рассчитать СКПФ сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ;

    2. качественно, с учетом найденных в п. а) параметров, изобразить сигналы и спектры на входе и выходе дискретизатора АЦП.

  4. Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования:

    1. рассчитать интервал квантования, пороги и уровни квантования, СКПК;

    2. построить в масштабе характеристику квантования.

  5. Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе двоичного ДКС:

    1. рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность двоичного дискретного источника;

    2. построить в масштабе графики, рассчитанных закона и функции распределения вероятностей.

  6. Закодировать значения двоичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода; кроме того:

    1. рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ;

    2. изобразить качественно на одном графике сигналы в четырех сечениях АЦП: вход АЦП, выход дискретизатора, выход квантователя, выход АЦП.

  7. Полагая, что для передачи ИКМ сигнала по НКС используется гармонический переносчик:

    1. рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра;

    2. построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра.

  8. Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношения сигнал-шум:

    1. рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС;

    2. построить в масштабе четыре графика ФПВ мгновенных значений и огибающих УГП, и суммы гармонического сигнала с УГП.

  9. С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:

    1. рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС. показатель эффективности передачи сигнала дискретной модуляции по НКС;

    2. изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи. когда он выносит ошибочные решения.

  10. Рассматривая отклик декодера ПРУ как случайный дискретный сигнал на выходе -ичного ДКС:

    1. рассчитать распределение вероятностей дискретного сигнала на выходе декодера, скорость передачи информации по -ичного ДКС, относительные потери в скорости передачи информации по -ичного ДКС;

    2. построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя.

  11. Полагая ФНЧ на выходе ЦАП приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:

    1. рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, СКПП, ССКП и ОСКП;

    2. качественно изобразить сигналы на выходе декодера и интерполятора ЦАП, а также восстановленного сообщения на выходе системы электросвязи.

  12. В виду того, что выбор начального энергетической ширины спектра исходного сообщения не приводит к минимуму ОСКП, решить оптимизационную задачу: с помощью ЭВМ определить оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления.

Привести блок-схему программы решения этой задачи на ЭВМ, распечатку программы, составленную на (выбранном самостоятельно) алгоритмическом языке, а также распечатку графика зависимости ОСКП от энергетической ширины спектра сообщения.

Непрерывное сообщение А(t), наблюдаемое на выходе источника сообщений (ИС), представляет собой реализацию стационарного гауссовского случайного процесса с нулевым средним и известной функцией корреляции ВА(t). Данное сообщение передается в цифровом виде в системе электросвязи.

Исходные данные.

Исходные данные для расчетов приведены в таблице, где РА=А2 – мощность (дисперсия) сообщения,  – показатель затухания функции корреляции, L – число уровней квантования, G0 – постоянная энергетического спектра шума НКС, h2 – отношение сигнал-шум (ОСШ) по мощности на входе детектора.


ИС; АЦП; L=8
ПДУ
НКС







PA, B2

, c-1
Способ

пере-

дачи
Частота, МГц

G0, Втс

h02

Способ

приема
Функция корреляции сообщения ВА(t)

f0
f1




2.7

32

АМ

1.9



0,0004

16

НП


=103


Структурная схема системы электросвязи


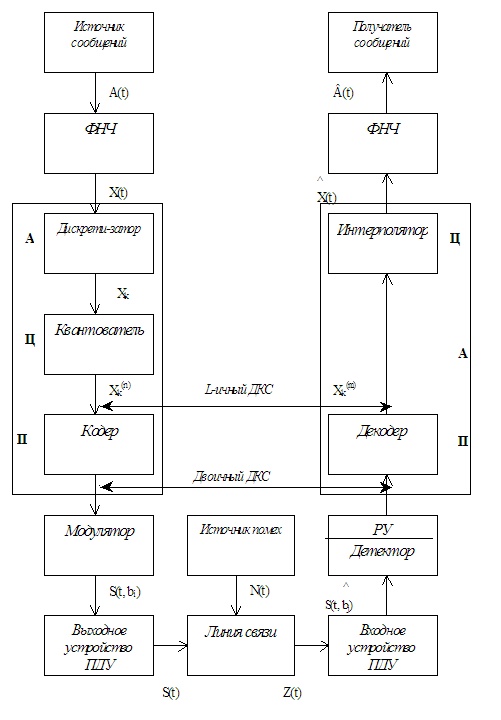
Рис.1





2. По заданной функции корреляции исходного сообщения:

2. а) Рассчитать интервал корреляции, спектр плотности мощности и начальную энергетическую ширину спектра


2. б) Построить в масштабе графики функции корреляции и спектра плотности мощности, отметив на них найденные в 2. а) параметры

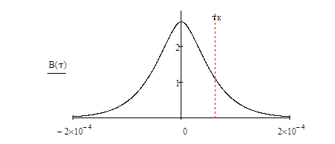
Найдем интервал корреляции:



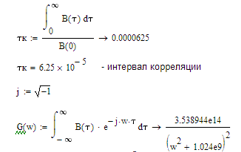
-плотность мощности сообщения

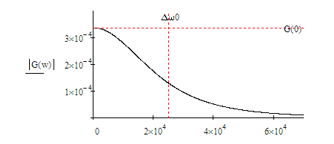
Построим энергетический спектр. т.е. спектр плотности мощности сообщения:

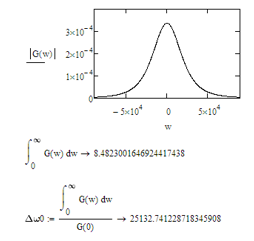Графически найдем максимальное значение энергетического спектра:



-максимальное значение

Энергетическая ширина сообщения



Спектр плотности мощности сообщения:



Функция корреляции сообщения:




3. Исходное сообщение воздействует на идеальный фильтр нижних частот с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения.

3. а) Рассчитать среднюю квадратичную погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ.



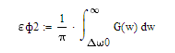
Средняя квадратическая погрешность фильтрации


Найдем среднюю мощность отклика ИФНЧ:





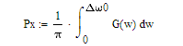
Рассчитаем частоту и интервал временной дискретизации отклика ИФНЧ:



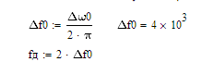
Частота временной дискретизации равна:


Интервал временной дискретизации



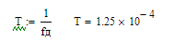
4. Пологая, что последовательность дискретных отсчетов на выходе дискретизатора далее квануется по уровню с равномерной шкалой квантования, найти:

4. а) интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования (СКПК)



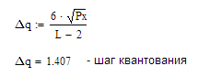
Пороги квантования:



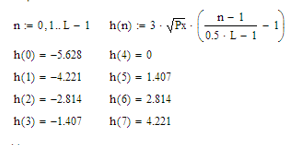
Уровни квантования:



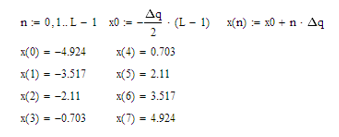
Вычислим среднеквадратическую погрешность квантования:


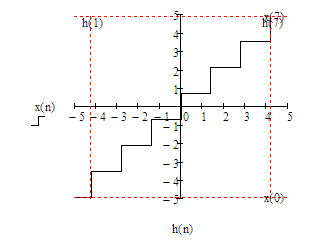
4. Построим характеристику квантования:

Характеристика квантования:



5.а) Рассмотрим отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L-ичного дискретного канала связи.

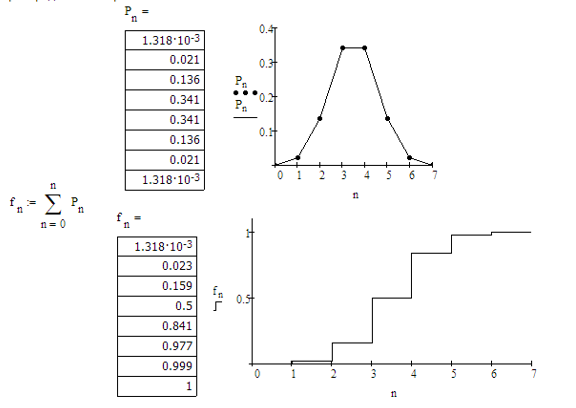
5.б) Рассчитать закон и функцию распределения вероятности квантованного сигнала, а так же энтропию, производительность и избыточность L-ичного дискретного источника.



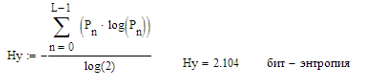
Производительность или скорость ввода информации в ДКС определяется соотношением:



5.б) Построить в масштабе графики рассчитанных законах и функции распределений вероятностей:



6. Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний:
Кодовые комбинации вероятности:



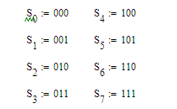
Таблица кодовых расстояний:

Смотрите также файлы