Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске.Истоки теории вероятностей: страховое дело, азартныеигры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров.Содержание курса алгебры в 7 классе.1. Выражения, тождества, уравнения. Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнений с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.2. Функции. Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и ее график.3. Степень с натуральным показателем. Степень с натуральным показателем и ее свойства. Одночлен. Функции у = 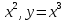и их графики.4. Многочлены. Многочлен. Сложение, вычитание и умножение многочленовРазложение многочленов на множители.5. Формулы сокращенного умножения. Формулы 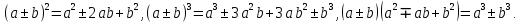Применение формул сокращенного умножения в преобразовании выражений.6. Системы линейных уравнений. Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений. 7. Повторение.Содержание курса алгебры в 8 классе.1. Рациональные дроби. Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у = 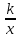и ее график.2. Квадратные корни. Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция у = 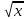, ее свойства и график.3. Квадратные уравнения. Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.4. Неравенства. Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближение. Линейные неравенства с одной переменной и их системы.

---

5. Степень с целым показателем. Элементы статистики. Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.6. Повторение.Содержание курса алгебры в 9 классе.1. Свойства функций. Квадратичная функция. Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = 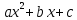, ее свойства и график. Степенная функция.2. Уравнения и неравенства с одной переменной. Целые уравнения. Дробные рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов.3. Уравнения и неравенства с двумя переменными. Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.4. Прогрессии. Арифметическая и геометрическая прогрессии. Формула n – го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.5. Элементы комбинаторики и теории вероятностей. Комбинаторное правило умножения. Перестановки, размещения, сочетания. Относительная частота и вероятность случайного события.

5. 
   Планируемые результаты изучения курса алгебры в 7-9 классах
   

РАЦИОНАЛЬНЫЕ ЧИСЛАВыпускник научится:1) понимать особенности десятичной системы счисления;2) владеть понятиями, связанными с делимостью натуральных чисел;3) выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;4) сравнивать и упорядочивать рациональные числа;5) выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применять калькулятор;6) использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.Выпускник получит возможность:7) познакомиться с позиционными системами счисления с основаниями, отличными от 10;8) углубить и развить представления о натуральных числах и свойствах делимости;9) научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛАВыпускник научится:1) использовать начальные представления о множестве действительных чисел;

---

2) владеть понятием квадратного корня, применять его в вычислениях.Выпускник получит возможность:3) развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;4) развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).ИЗМЕРЕНИЯ, ПРИБЛИЖЕНИЯ, ОЦЕНКИВыпускник научится:1) использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.Выпускник получит возможность:2) понять, что числовые данные, которые используютсядля характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;3) понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯВыпускник научится:1) владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;2) выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;3) выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;4) выполнять разложение многочленов на множители.Выпускник получит возможность:5) научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;6) применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).УРАВНЕНИЯВыпускник научится:1) решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;2) понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;3) применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.Выпускник получит возможность:4) овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики

---

, смежных предметов, практики;

5) применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.

НЕРАВЕНСТВА

Выпускник научится:

1) понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;

2) решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;

3) применять аппарат неравенств для решения задач из различных разделов курса.

Выпускник получит возможность научиться:

4) разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;

5) применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.

ОСНОВНЫЕ ПОНЯТИЯ. ЧИСЛОВЫЕ ФУНКЦИИ

Выпускник научится:

1) понимать и использовать функциональные понятия и язык (термины, символические обозначения);

2) строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;

3) понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.

Выпускник получит возможность научиться:

4) проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);

5) использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.

ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Выпускник научится:

1) понимать и использовать язык последовательностей (термины, символические обозначения);

2) применять формулы, связанные с арифметической и геометрической прогрессиями, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числес контекстом из реальной жизни.

Выпускник получит возможность научиться:

3) решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессий, применяя при этом аппарат уравнений и неравенств;

4) понимать арифметическую и геометрическую прогрессии как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.

---

ОПИСАТЕЛЬНАЯ СТАТИСТИКАВыпускник научится использовать простейшие способы представления и анализа статистических данных.Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬВыпускник научится находить относительную частоту и вероятность случайного события.Выпускник получит возможность приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов.КОМБИНАТОРИКАВыпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.Выпускник получит возможность научиться некоторым специальным приёмам решения комбинаторных задач.

6. 
   Нормы оценки знаний, умений и навыков обучающихся
   

Оценка письменных контрольных работ, обучающихся по математике.Ответ оценивается отметкой «5», если:

• 
  работа выполнена полностью;
  
• 
  в логических рассуждениях и обосновании решения нет пробелов и ошибок;
  
• 
  в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
  

Отметка «4» ставится в следующих случаях:

• 
  работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
  
• 
  допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
  

Отметка «3» ставится, если:

• 
  допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
  

Отметка «2» ставится, если:

• 
  допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
  

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

---

Смотрите также файлы

• Отчетность это сведения об имущественном и финансовом положении организации и о конечных результатах ее хозяйственной деятельности в определенном периоде.doc

• Проблема толкования права относится к общетеоретическим основам государства и права. Реализация и особенно применение правовых норм невозможны без предварительного познания смысла правовых установлений.rtf

• Баллада о матери (41й) декл. Ольга Киевская.docx

• Научный руководитель др филос наук профессор В. В. Шалин дипломная работа интеграция российского образовательного процесса на основе болонских соглашений в европейскую систему подготовки кадров для социальной работы.doc

• Лабораторная работа по дисциплине Технологическое оборудование и перспективы его развития На тему Котлетоформовочная машина мфк2240.docx