Произведём построение линий влияния поперечной силы.

Сечение: Ордината:

x = 0 Q₀ = 1

x = 0,1 ℓ Q₁ = 0,9

x = 0,2 ℓ Q₂ = 0,8

x = 0,3 ℓ Q₃ = 0,7

x = 0,4 ℓ Q₄ = 0,6

x = 0,5 ℓ Q₅ = 0,5

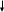
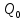
1 ℓ

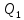0.9ℓ



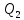
0.8ℓ



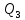
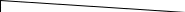
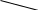0.7 ℓ



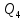0.6ℓ



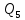
0.5ℓ

Рисунок 5-Линии влияния поперечной силы

Определим расчётные усилия от сосредоточенных сил с учётом того, что одна из них располагается над вершиной линии влияния.

Q₀ = Q₀ (1+

---

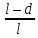
)*P = 1*(1+ 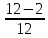)*5 = 9,2(T)

Q₁ = Q₁(1+ 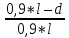)*P = 0,9*(1+ 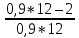)*5= 8,2(T)

Q₂ = Q₂(1+ 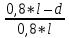)*P = 0,8*(1+ 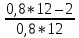)*5 = 7,2(T)

Q₃ = Q₃(1+ 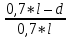)*P = 0,7*(1+ 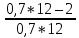)*5 = 6,2(T)

Q₄ = Q₄(1+ 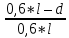)*P = 0,6*(1+ 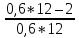)*5 = 5,2(T)

Q₅ = Q₅(1+ 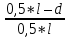)*P = 0,5*(1+ 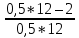)*5 = 4,2(T)

На основании расчетов строим эпюру наибольшего усилия от подвижной нагрузки в разных сечениях.



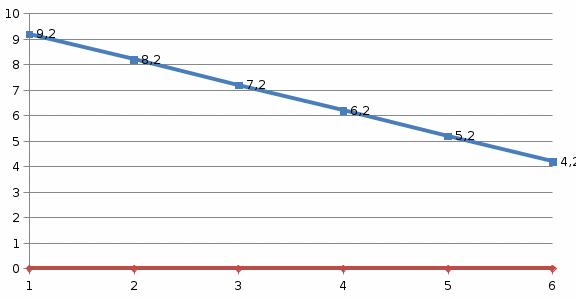
Рисунок 6 - Эпюра наибольших значений поперечной силы от подвижной нагрузки в разных сечениях балки

Определим поперечные силы от собственного веса балки в её разных сечениях.

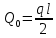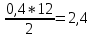= (Т)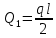

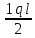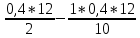- = =1,95(Т)

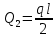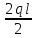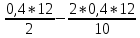- = =1,44(Т)

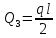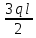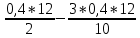- = =0,96(Т)

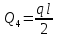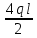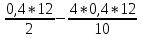- = =0,48(Т)

-

---

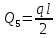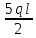
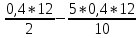= =0(Т)

На основании расчетов строим эпюру поперечной силы от равномерной распределенной нагрузки.



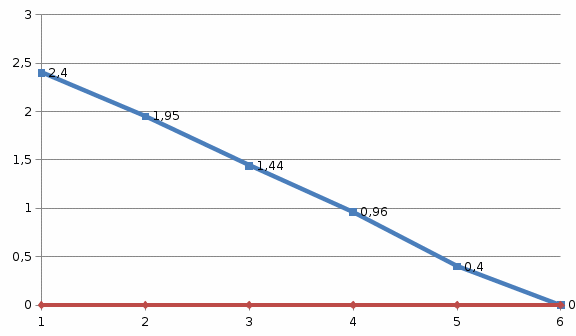
Рисунок 7-Эпюра значений силы от собственного значения балки
Определим суммарные расчетные значения поперечных сил от собственного веса и равномерно распределенных нагрузок.

=9,2+2,4=11,6(т)

=8,2+1,95=10,15(т)

=7,2+1,44=8,64(т)

=6,2+0,96=7,16(т)

=5,2+0,48=5,68(т)

=4,2+0=4,2(т)

На основании расчетов строим эпюру сосредоточенных и распределенных нагрузок.



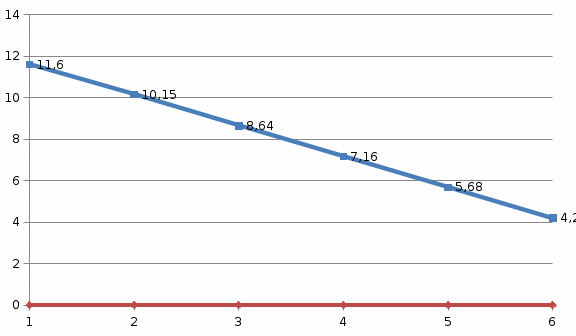
Рисунок 8 - Эпюра собственного веса и распределенных нагрузок

---

1.2 Определение высоты балки
Находим требуемую наименьшую высоту балки из условия нормы жёсткости.

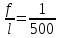от сосредоточенных грузов.

Основное допускаемое напряжение для стали Ст 3 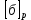=12 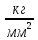, т.к. это напряжение соответствует суммарному моменту М=32,2 Т*м , то от момента 25 Т*м вызванного сосредоточенными грузами напряжение будет составлять 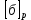= =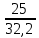 0,8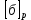 эту величину и следует учитывать вместо 12 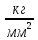при определении требуемой высоты балки.

Прогиб от двух сосредоточенных грузов расположенных симметрично в полёте равен



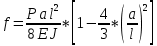
E-модуль упругости зависит от состава материала, для стали Ст3 Е=

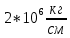
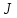- коэффициент устойчивости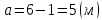



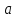-расстояние от опоры до груза

Р 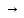М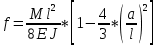

из формулы W=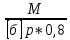

М=W*0,8 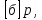из формулы W 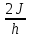, М=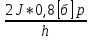

????= *

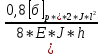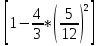
отсюда выражаем высоту

h= * = *

---

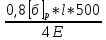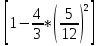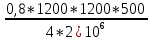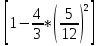
=72*0,77= =55(см)

Вывод ꞉ таким образом минимальная высота балки h=55 см .Чтобы определить требуемую высоту балки из условия ее наименьшего сечения нужно задаться толщиной вертикального листа. Для этого воспользуемся приближенным соотношением.



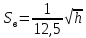
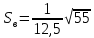=0,59

принимаем толщину вертикального листа 0,6 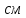или 6мм

Требуемая высота балки из условия наименьшего веса для двутаврового профиля определяется по формуле

h=1.3 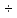1.4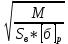

h=1,3 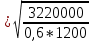=87,1(см)

Вывод꞉ Так как полученное значение требуемой высоты балки 87,1 см больше требуемой минимальной высоты балки ,то в расчётах при подборе сечения балки следует принять высоту h=55см

Высоту вертикального листа находим из соотношения

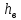=(0,95 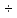0,98)*h

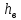=0,98*55=53,9(см) принимаем 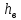=53(см)


550



53000

6

5400





455




Рисунок 9 - Подобранный профиль балки
1.3 Определение момента инерции
Находим требуемый момент инерции поперечного сечения двутавровой балки

---

Смотрите также файлы

• Контрольная работа по Философия наименования дисциплины 1,14,27,40,53. варианты Преподаватель А. Ю. Коловская подпись, дата инициалы, фамилия.docx

• Символы России.docx

• Тактика фельдшера выездной бригады при неуточнённой почечной колике.docx

• углов.docx

• Решение по делу, может по своей инициативе или по заявлению лиц, участвующих в деле, принять дополнительное решение суда в случае, если.docx