Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ)

Кафедра теории электрической связи

КУРСОВАЯ РАБОТА

по дисциплине
Общая теория связи

Выполнил студент

Группы БИК2105

Ширинянц Никита

Вариант №21

Москва 2023

Техническое задание

Непрерывное сообщение А(t), наблюдаемое на выходе источника сообщений (ИС), представляет собой реализацию стационарного гауссовского случайного процесса с нулевым средним и известной функцией корреляции В_А(t). Данное сообщение передается в цифровом виде в системе электросвязи.

Исходные данные

Исходные данные для расчетов приведены в таблице, где Р_А=_А² – мощность (дисперсия) сообщения,  – показатель затухания функции корреляции, L – число уровней квантования, G₀ – постоянная энергетического спектра шума НКС, h² – отношение сигнал-шум (ОСШ) по мощности на входе детектора.

ИС; АЦП; L=8		ПЦУ			НКС
PA, B	, c-1	Способ пере- дачи	Частота, МГц		G0, Втс	h02	Способ приема		Функция корреляции сообщения ВА(t)
			f0	f1
4,4	7	ОФМ	3,0	2,95	0,0022	6,1	СФ		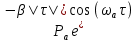, =103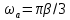

---

1. 
   Изобразить структурную схему системы электросвязи и пояснить назначение её отдельных элементов.
   

Источник сообщений – это некоторый объект или система, информацию о состоянии или поведении которого необходимо передать на некоторое расстояние. Причем под объектом или системой подразумевают человека, ЭВМ, автоматическое устройство или что-либо другое. Передаваемая от ИС информация является непредвиденной для получателя. Поэтому количественную меру передаваемой по системе информации в теории электросвязи выражают через статистические (вероятностные) характеристики сообщений (сигналов). Сообщение – есть физическая форма представления информации. Часто сообщение представляют в виде изменяющегося во времени тока или напряжения, отображающих передаваемую информацию.

В ПДУ сообщение вначале фильтруется с целью ограничения его спектра некоторой верхней частотой F_В. Это необходимо для эффективного представления отклика ФНЧ x(t) в виде последовательности отсчетов x_k=x(t_k=kT), k=0,1,2,…, наблюдаемых на входе дискретизатора. Фильтрация связана с внесением погрешности _ф(t), отображающий ту часть сообщения, которая подавляется ФНЧ. Далее отсчеты x_k квантуются по уровню. Процесс квантования связан с нелинейным преобразованием непрерывнозначных отсчетов x_k в дискретнозначные x_k⁽ⁿ⁾, n= 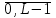, что также привносит погрешность, называемую погрешностью (шумом) квантования _q(t). Квантованные уровни y_k=x_k⁽ⁿ⁾ затем кодируются двоичным безызбыточным кодом.

БВО – блок внесения относительности.

Последовательность кодовых комбинаций 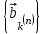образует сигнал ИКМ, который подводится к модулятору – устройству, предназначенному для согласования источника сообщений с используемой линией связи. Модулятор формирует канальный сигнал S(t,b_i), который представляет собой электрическое или электромагнитное колебание, способное распространяться по линии связи и однозначно связанное с передаваемым сообщением (в данном случае с сигналом ИКМ). Сигнал S(t,b_i) создается в результате модуляции – процесса изменения одного или нескольких параметров переносчика по закону модулирующего ИКМ сигнала. При использовании гармонического переносчика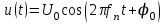

---

различают сигналы амплитудной, частотной и фазовой модуляции.

Для предотвращения внеполосных излучений в одноканальной или при организации многоканальной связи, а также для установления требуемого отношения сигнал-шум (ОСШ) на входе приемника канальный сигнал фильтруется и усиливается в выходных каскадах ПДУ.

Сигнал S(t) c выхода ПДУ поступает в линию связи, где на него накладывается помеха N(t). На вход ПРУ воздействует смесь 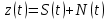переданного сигнала и помехи. Здесь во входных каскадах ПРУ принятый сигнал фильтруется и подается на детектор.

При демодуляции из принятого сигнала 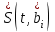выделяется закон изменения информационного параметра, который в нашем случае пропорционален сигналу ИКМ. При этом для опознавания переданных двоичных символов на выход демодулятора подключается решающее устройство (РУ). При передаче двоичных сигналов b_i=0 или 1, i=0,1, по ДКС наличие помех в НКС приводит к неоднозначным решениям (ошибкам) РУ, что, в свою очередь, вызывает несоответствие переданных 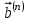и принятых 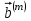кодовых комбинаций.

Наконец, для восстановления переданного непрерывного сообщения A(t), т.е. получения его оценки 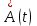, принятые кодовые комбинации подвергаются кодированию, интерполяции и низкочастотной фильтрации. При этом в декодере по двоичным кодовым комбинациям восстанавливаются L-ичные уровни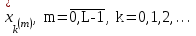

Наличие ошибок в двоичном ДКС приводит к ошибкам передачи в L-ичном ДКС и, соответственно, к возникновению шума передачи _п(t). Совокупное действие погрешности фильтрации, шумов квантования и передачи приводит к неоднозначности между переданными и принятыми сообщениями .

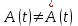В системах передачи непрерывных сообщений верность (качество) передачи считается удовлетворительным, если минимальная суммарная относительная СКП восстановления не превосходит допустимую, т.е.

---

2. 
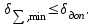
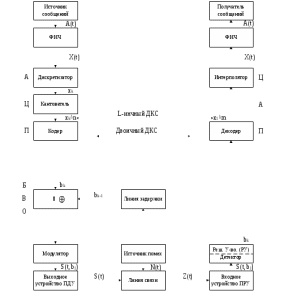
   По заданной функции корреляции исходного сообщения:
   

а) рассчитать интервал корреляции, спектр плотности мощности и начальную энергетическую ширину спектра сообщения
τ_{к =}

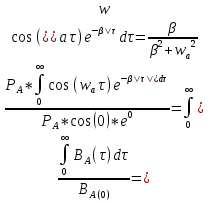
Подставив свои значения, получаем:





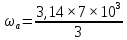
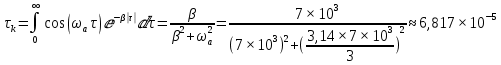
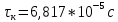
Спектр плотности мощности


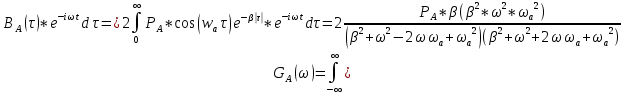
Начальная энергетическая ширина спектра сообщения:









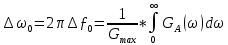
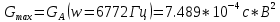
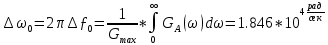
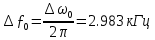
б) построить в масштабе графики функции корреляции и спектра плотности мощности; отметить на них найденные в п. а) параметры



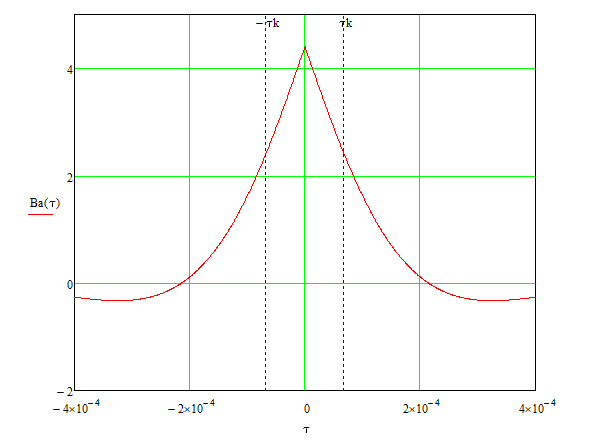
График функции корреляции



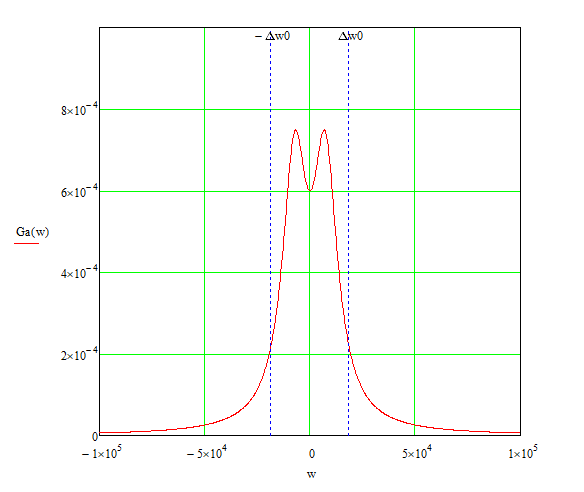
График спектра плотности мощности

2. 
   Считая, что исходное сообщение воздействует на идеальный фильтр нижних частот (ИФНЧ) с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения:
   

а) рассчитать среднюю квадратическую погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ
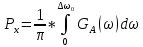=3.242B²
Найдем среднюю квадратическую погрешность фильтрации (СКПФ)



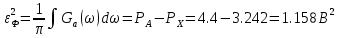
Частота и интервал временной дискретизации отклика ИФНЧ:



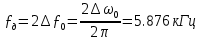
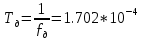с

б) качественно, с учетом найденных в п. а) параметров, изобразить сигналы и спектры на входе и выходе дискретизатора АЦП.

---

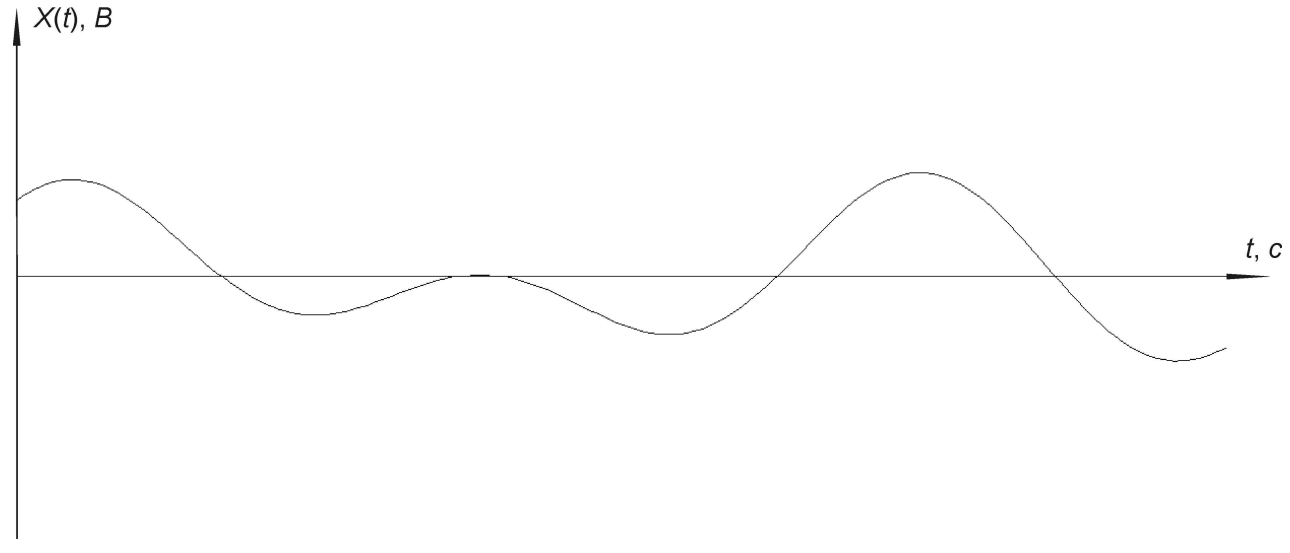
Сигнал входа АЦП



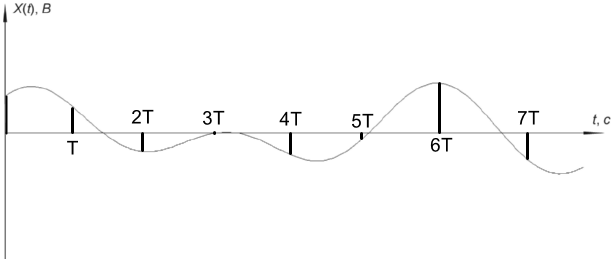
Сигнал на выходе дискретизатора



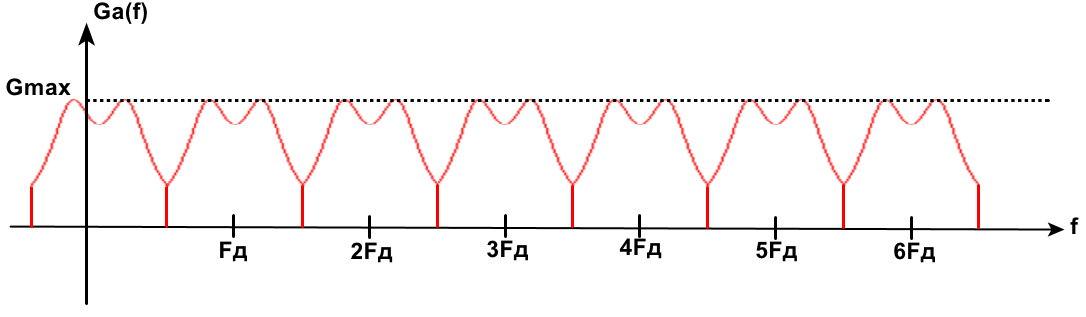
Спектр сигнала на выходе дискретизатора

2. 
   Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования:
   

а) рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования (СКПК)

Шаг квантования можно рассчитать следующим образом:

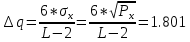В

Пороги квантования:

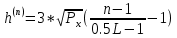, n = 1…L-1

n	0	1	2	3	4	5	6	7	8
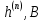	-∞	-5.4	-3.6	-1.8	0	1.8	3.6	5.4	∞

Уровни квантования:

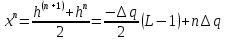n= 0…L-1

n	0	1	2	3	4	5	6	7
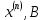	-6.3	-4.5	-2.7	-0.9	0.9	2.7	4.5	6.3

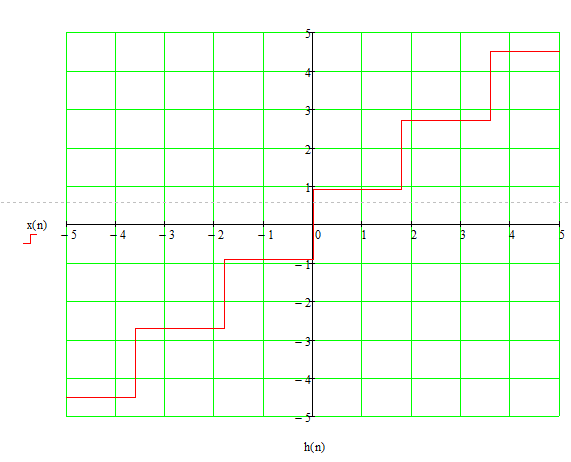
Характеристика квантователя
Средняя квадратичная погрешность:

---

Смотрите также файлы

• Казанский государственный медицинский университет кафедра госпитальной терапии.docx

• Общеобразовательная школаинтернат основного общего образования спортивного профиля.docx

• Контрольная работа по дисциплине Конституционное право Институт непрерывного и дистанционного образования.docx

• Классный час Класс 4 Количество присутствующих Количество отсутствующих.docx

• Инновационная экономика перспективы развития и совершенствования, 4 (54), 2021 65.pdf