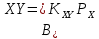
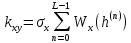
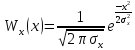
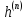-5.4	-3.6	-1.8	0	1.8	3.6	5.4
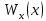	0.00246	0.03	0.134	0.222	0.134	0.03	0.00246

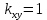
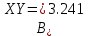
СКП квантования:







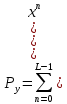
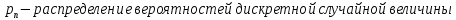
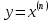
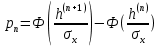, где Ф(v) – табулированная функция Лапласа

Ф(v) =



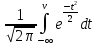
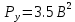
Мощность шума квантования:

2. 
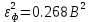
   Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L-ичного дискретного канала связи (ДКС):
   

а) рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность L-ичного дискретного источника

Соотношение вероятностей рассчитывается как

,

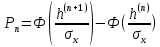Ф(v) = 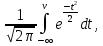Ф() – табулированная функция Лапласа

n	0	1	2	3	4	5	6	7
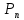	1.318e-3	0.021	0.136	0.341	0.341	0.136	0.021	1.318e-3

---

Интегральное распределение вероятностей

F_n =

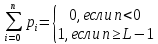
Энтропия



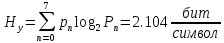
Производительность или скорость ввода информации в ДКС:



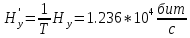
Избыточность последовательности источника:





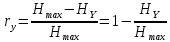
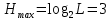
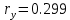
График закона распределения вероятности на выходе



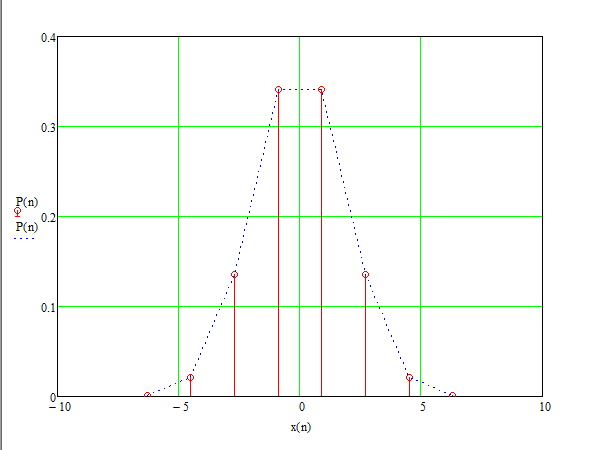
График функция распределения вероятностей



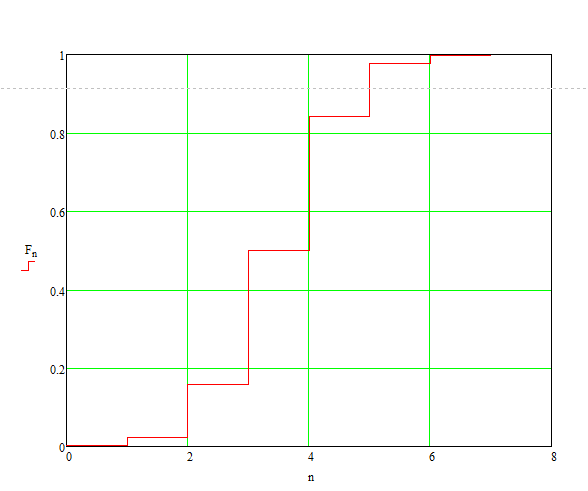
Закон распределения вероятностей
6.Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода

Таблица кодовых расстояний

	000	001	010	011	100	101	110	111
000	0	1	1	2	1	2	2	3
001	1	0	2	1	2	1	3	2
010	1	2	0	1	2	3	1	2
011	2	1	1	0	3	2	2	1
100	1	2	2	3	0	1	1	2
101	2	1	3	2	1	0	2	1
110	2	3	1	2	1	2	0	1
111	3	2	2	1	2	1	1	0

---

а) рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ

Так как среднее число нулей 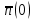и среднее число единиц 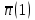в сигнале ИКМ одинаково, то и вероятности их появления одинаковы: p(0)=p(1)=0.5
Длительность одного импульса

=

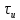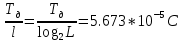
Ширина спектра элементарного прямоугольного импулься обратно пропорциональна длительности .

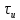Начальная ширина спектра ИКМ:





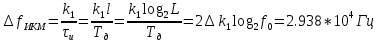
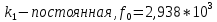
б) Изобразить качетсвенно на одном графике сигналы в четырех сечениях АЦП: вход АЦП, выход дискретизатора, выход квантователя.


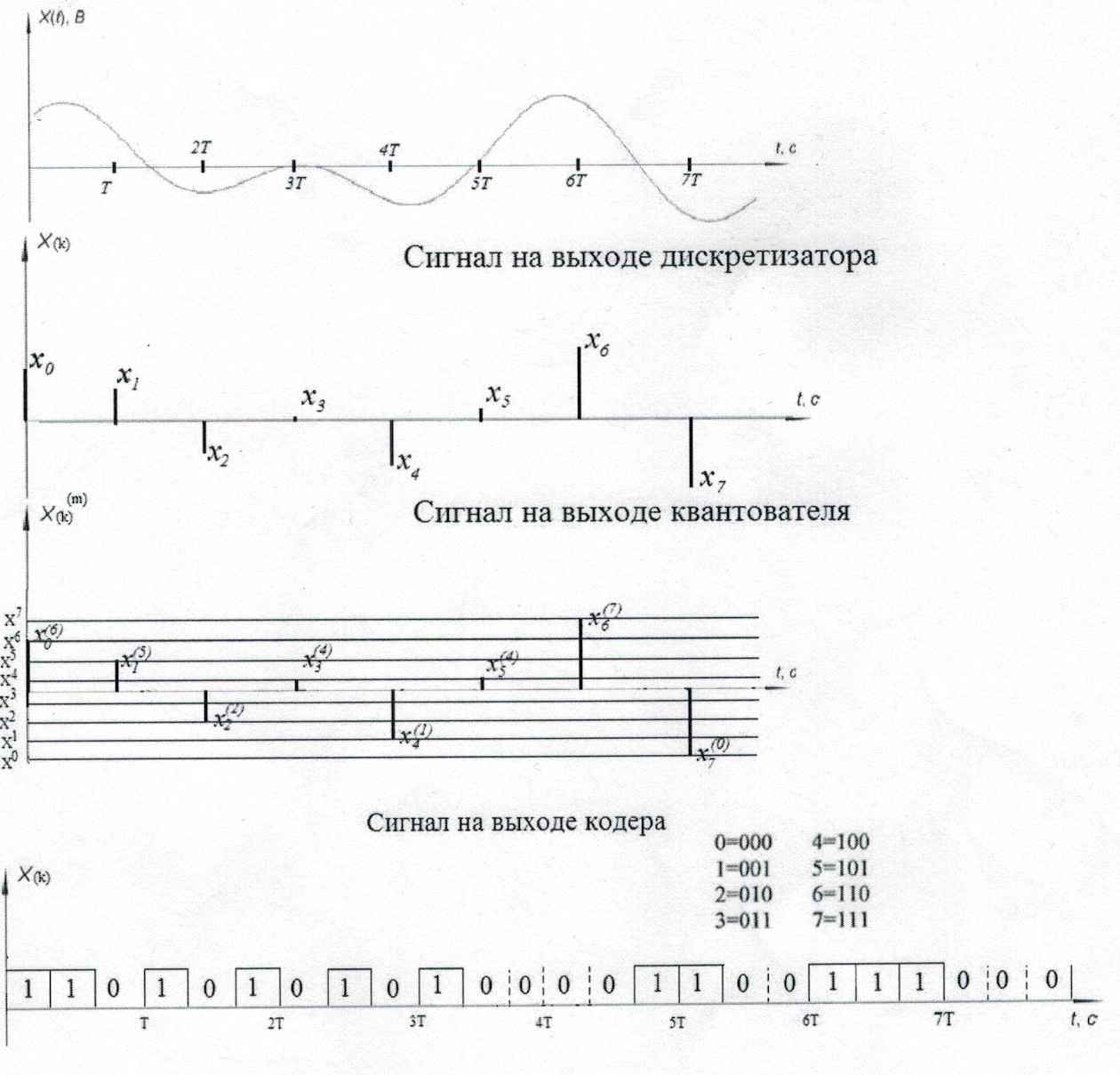
7 Полагая, что для передачи ИКМ сигнала по непрерывному каналу связи (НКС) используется гармонический переносчик:

а) рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра.

Сигнал ДОФМ представляется в виде:








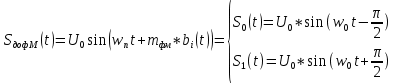
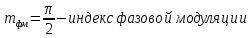
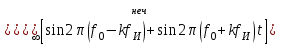
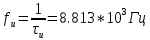
Начальная ширина спектра:



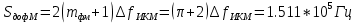
б) построить в масштабе график нормированного спектра сигнала дискретной модуляции .

Для вычисления нормированного спектра будем рассчитывать нормированные значения амплитуд гармоник:


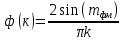
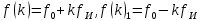–гармоники на частотах

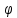k	(k)	f(k)	f(k)1
1	0.637	3.009*106	2.974*106
3	0.212	3.026*106	2.956*106
5	0.127	3.044*106	2.938*106
7	0.091	3.062*106	2.921*106
9	0.071	3.079*106	2.903*106
11	0.058	3.097*106	2.885*106
13	0.049	3.115*106	2.868*106
15	0.042	3.132*106	2.85*106
17	0.037	3.15*106	2.974*106

---

Нормированный спектр сигнала дискретной модуляции


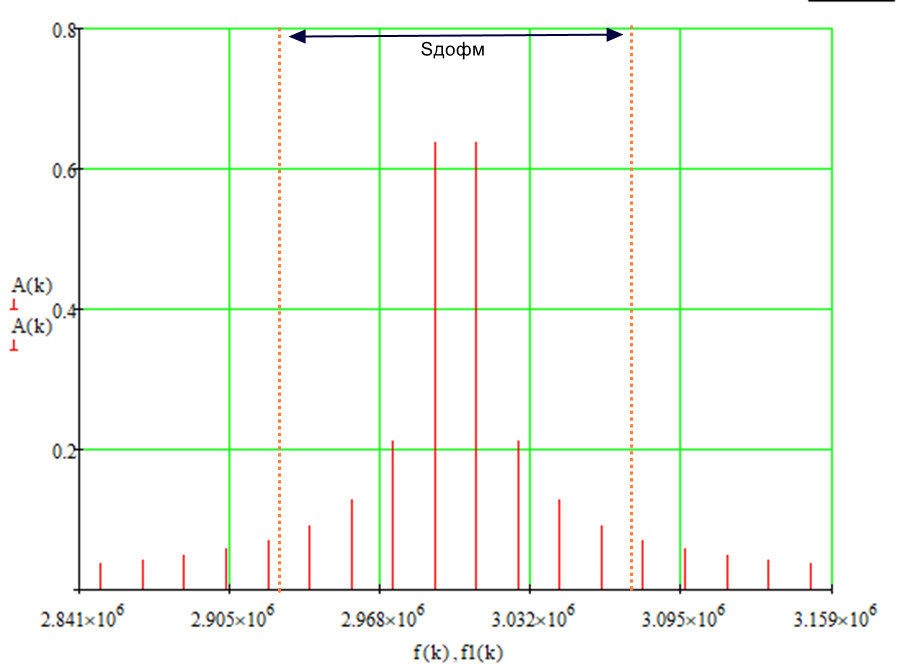
8.Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал-шум:
а) рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС

Белый шум- помеха с равномерным спектром

Мощность белого шума:

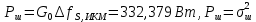
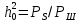-отношение сигнал/шум на входе детектора приемника

мощность сигнала дискретной модуляции: 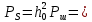2,028* 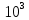Вт

мощность и амплитуда, в среднем приходящиеся на один двоичный символ:



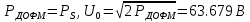
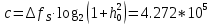бис/с-пропускная способность гауссовского НКС

б) построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП
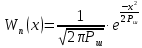– огибающая n (случайно изменяющаяся амплитуда) гауссовской помехи распределения по закону Рэлея.

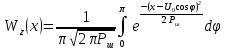- функция плотности вероятности мгновенных значений Z(t), если 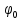распределена равномерно ( )



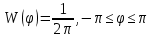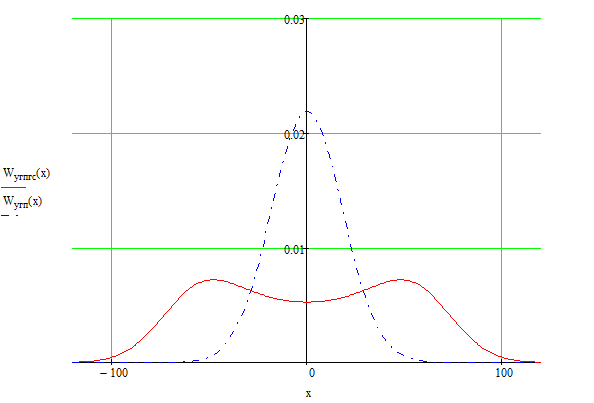
График ФПВ мгновенных значений УГП и суммы гармонического сиглала и УГП

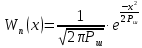– огибающая n (случайно изменяющаяся амплитуда) гауссовской помехи распределения по закону Рэлея.

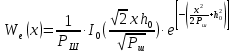- распределение Рэлея. Где I₀- модифицированная функция Бесселя нулевого порядка от мнимого аргумента.

---

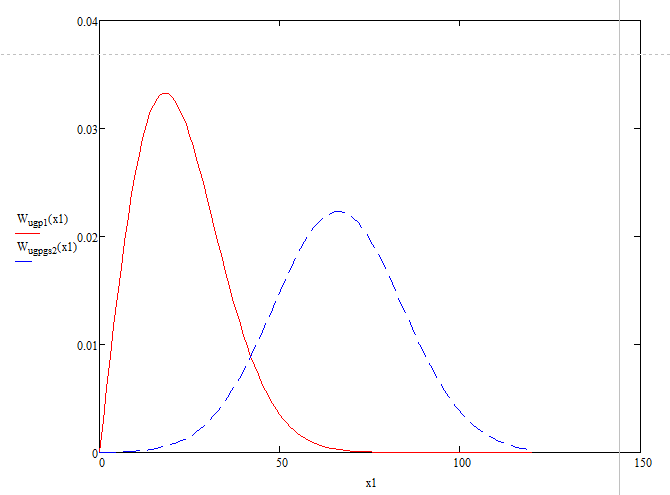
Графики огибающих УГП и суммы гармонического сигнала и УГП

9. 
   С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:
   

а) рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС

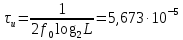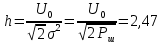с – ОСШ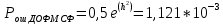

- вероятность ошибки для ДОФМ СФ

Р_{ош ДОФМ СФ}=Р_ош

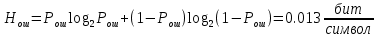- энтропия ошибочных решений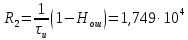

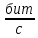– скорость передачи информации по дискретному каналу связи (для двоичного симметричного ДКС)

Так как вероятность ошибок Р_ош для различных видов сигналов зависят от h² на входе детектора, то и R2 зависит от ОСШ. Для сравнения скорости R2 при данном виде модуляции и способе приема с пропускной способностью НКС С вводят показатель эффективности:

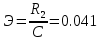- показатель эффективности системы передачи

б) изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи, когда он выносит ошибочные решения




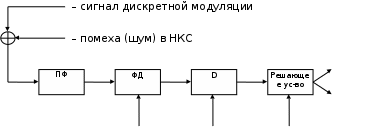
В сигналах с фазовой модуляцией (ФМ), знак выходного напряжения определяется фазой принятого сигнала в фазовом детекторе ФD.

П ри способе сравнения фаз(СФ), за счет линии задержки(ЛЗ) ОДФМ сигнал задерживается на время посылки τ_з= τ_и, совмещаются n-ая и (n-1)-ая посылки. Их фазы сравниваются в ФD. В результате восстанавливается сигнал с модуляцией по закону управляющих напряжений. К дискретизатору (D), подводится отклик детектора U(t), а так же последовательность дискретизирующих импульсов с периодом τ

---

Смотрите также файлы

• Казанский государственный медицинский университет кафедра госпитальной терапии.docx

• Общеобразовательная школаинтернат основного общего образования спортивного профиля.docx

• Контрольная работа по дисциплине Конституционное право Институт непрерывного и дистанционного образования.docx

• Классный час Класс 4 Количество присутствующих Количество отсутствующих.docx

• Инновационная экономика перспективы развития и совершенствования, 4 (54), 2021 65.pdf