Файл: Используя формулы Муавра найти все корни, и записать их в алгебраической форме.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 14

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.






Используя формулы Муавра найти все корни   , и записать их в алгебраической форме







 . Берём 







При этом 

Найти матрицу, обратную матрице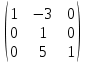 

Для вычисления обратной матрицы запишем данную матрицу, дописав к ней справа единичную матрицу: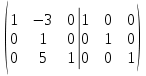



Теперь, что бы найти обратную матрицу, используя элементарные преобразования над строками матрицы, преобразуем левую часть полученной матрицы в единичную. К 1 строке добавляем вторую строку, умноженную на 3, от 3 строки отнимаем вторую строку, умноженную на 5: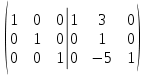



Ответ: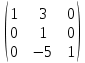 

Найти каноническое уравнение прямой, проходящей через точку A(1, 2, 3) и перпендикулярную плоскости с общим уравнением 5x – 3y – 12z – 7 = 0

Общее уравнение плоскости имеет вид:

Ax+By+Cz+D=0

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку   и имеющий направляющий вектор q(l, m, n) имеет следующий вид:



Для того, чтобы прямая была ортогональна плоскости, направляющий вектор q(l, m, n) прямой должен быть коллинеарным нормальному вектору n(A,B,C) плоскости. Следовательно, в качестве направляющего вектора прямой можно взять нормальный вектор плоскости

Таким образом, уравнение прямой, проходящей через точку   и ортогональный плоскости имеет следующий вид:



Подставляя координаты точки и координаты нормального вектора плоскости в (3), получим:



Ответ: Каноническое уравнение прямой: 

Решить СЛАУ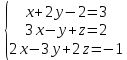 

Перепишем систему уравнений в матричном виде и решим методом Гаусса: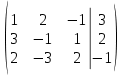



От 2 строки отнимаем 1 строку, умноженную на 3. От 3 строки отнимаем 1 строку, умноженную на 2: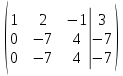



2 строку делим на -7: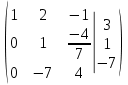



От 1 строки отнимаем 2 строку, умноженную на 2. К 3 строке добавляем 2 строку, умноженную на 7: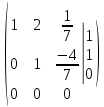



Ответ: Система имеет множество решений: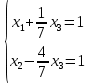



Найти канонический вид квадратичной формы 

Выпишем матрицу квадратичной формы:

 = 0







 ; 



Ответ: 

Смотрите также файлы