Файл: 2. математические модели в технической диагностике Основные понятия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 101
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
S6 S7 S3 S4 S1 S2
6 6 6 6
1 0 0 0 1 0 1 0
S0 S5 S6 S7 S4 S3 S1 S2
2
1 0
S7 S6
Рис. 2.12. Алгоритм определения состояния объекта
И функциональная модель, и граф причинно-следственных связей в конечном итоге определяют математическую модель объекта в виде таблицы состояний. Задание оператора объекта диагностирования в табличной форме достаточно удобно. Однако в ряде случаев (например, когда параметры определены на непрерывном множестве) такое представление оператора невозможно. В таких ситуациях математическая модель может быть представлена в виде аналитических зависимостей между входными возмущениями, параметрами технического состояния и диагностическими параметрами.
В технической диагностике математические (диагностические) модели объектов, устанавливающие связь между входными возмущениями, параметрами технического состояния и диагностическими параметрами (признаками) в виде аналитических зависимостей (уравнений) называются аналитическими моделями. Эти аналитические модели (зависимости) чаще всего могут быть представлены в виде алгебраических или дифференциальных уравнений. Познакомимся с некоторыми подобными моделями.
2.5 Аналитические модели в виде дифференциальных уравнений
Наиболее часто аналитические модели в виде дифференциальных уравнений применяются в вибрационной диагностике. Это связано с тем, что вибрация (упругие механические колебания) механизмов - это их реакция на действие приложенных возмущающих сил, а основным математическим аппаратом для анализа вибрации (упругих механических колебаний) технических устройств является аппарат дифференциальных уравнений [5, 7, 9, 13].
Вибрационное (колебательное) поведение технических систем описывается дифференциальным уравнением (системой уравнений), у которого (как правило) в правой части находится аналитическое выражение, определяющее зависимость возмущающих сил от времени. В левую часть этого уравнения (системы уравнений) помещены производные по времени перемещений точек механизма с коэффициентами, характеризующими инерционные (массовые), упругие (жесткостные) и демпфирующие (рассеивающие) свойства этого механизма. Отсюда следует, что анализ виброакустических процессов для целей диагностики позволяет выявить такие неисправности, которые приводят к изменению действующих на механизм возмущающих сил или к изменению инерционных, жесткостных и демпфирующих свойств этого механизма (например, разбалансировку роторов, нарушение соосности роторов, возникновение трещин, неисправности подшипниковых узлов и т.п.). Поясним это на простейшем примере.
Представим диагностируемый механизм в виде простой одномассовой колебательной системы (рис.2.13).
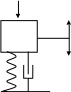F(t) F(t) - возмущающая внешняя сила;
m - масса системы;
m x(t) C - коэффициент жесткости системы;
h- коэффициент демпфирования в системе;
x(t)- перемещение центра масс по действием
C h возмущающей силы.
Рис. 2.13. Простейшая одномассовая колебательная система
Колебания центра масс этой системы описываются следующим дифференциальным уравнением:
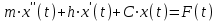. (2.9)
Общее решение этого уравнения, описывающее зависимость перемещения центра масс от времени, записывается в следующем виде:
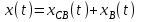, (2.10)
где xСВ(t) - определяет свободные колебания цента масс, а xВ(t) - вынужденные.
Для того чтобы в ходе решения уравнения (2.9) получить конкретные аналитические зависимости от времени свободных и вынужденных колебаний, необходимо определить в конкретном аналитическом виде зависимость от времени возмущающей силы [5, 20]. При изучении вибрационных процессов чаще всего используется представление как самих колебаний, так и действующих сил в виде ряда Фурье. Поэтому примем, что возмущающая сила, действующая на систему, является гармонической (т. е.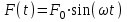
, где F0 - амплитуда возмущающей силы, - частота возмущающей силы). С учетом этого выражение (2.9) можно переписать в виде
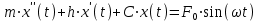. (2.11)
Решая это уравнение, получим, что свободные колебания являются затухающими и определяются выражением
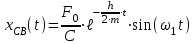, (2.12)
где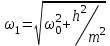
- частота свободных колебаний;
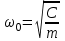- собственная частота колебаний системы.
Необходимо отметить, что в реальных системах m h, поэтому свободные колебания механических систем совершаются с частотой, практически равной собственной частоте системы (т.е.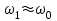
). Воспроизвести свободные колебания в реальных условиях можно путем тестового воздействия на объект коротким импульсом возмущающей силы, то есть ударом.
При возбуждении системы (см. рис. 2.13) ударом она будет совершать свободные колебания с частотой, равной собственной частоте системы. Амплитуда колебаний будет зависеть от соотношения между амплитудой силы и жесткостью системы. Скорость затухания колебаний будет определяться величиной соотношения демпфирования и массы в системе. Отсюда следует, что обнаружить неисправность объекта путем анализа его свободных колебаний можно в том случае, если эта неисправность вызовет изменение частоты свободных колебаний или скорости их затухания. Или, другими словами, если неисправность повлияет на динамические (жесткостные, демпфирующие, массовые) характеристики системы.
Если поведение системы описывается уравнением (2.11) и на нее постоянно действует гармоническая сила, то через определенный интервал времени свободные колебания затухнут, и система будет совершать только вынужденные колебания. Эти колебания будут также гармоническими, а их аналитическая зависимость определяется выражением
xВ(t) = X0 sin (t), (2.13)
где X0 - амплитуда вынужденных колебаний; - частота вынужденных колебаний.
Частота вынужденных колебаний равна частоте возбуждающей силы, а амплитуда колебаний зависит от амплитуды возбуждающей силы и коэффициента динамичности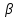
:
X0 = F0. (2.14)
Коэффициент динамичности зависит только от характеристик системы и для нашего случая определяется следующим соотношением:
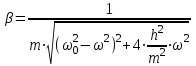(2.15)
Максимальное значение коэффициент динамичности принимает при равенстве частоты возбуждающей силы собственной частоте системы: = 0. Такое явление называется резонансом, и говорят, что система совершает резонансные колебания. Как следует из соотношения (2.15), амплитуда резонансных колебаний зависит от величины возбуждающей силы и демпфирующих свойств системы.
Приведенные соотношения свидетельствуют о том, что диагностика объектов путем анализа вынужденных колебаний возможна в том случае, если неисправности вызывают изменение возбуждающей силы (ее величины или частоты) или изменение динамических свойств самого объекта (массы, жесткости, демпфирования).
Представленные выше зависимости выходного сигнала (колебаний) описыва-ют только одно техническое состояние механизма (исправное) , для получения описаний неисправных состояний необходимо установить зависимости между параметрами силы (входным воздействием) и дефектами или зависимости между массой , жесткостью, демпфированием и дефектами, то есть для вибрационной диагностики характерно задание неявных моделей.
Реальные механизмы обладают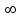
числом собственных форм и частот колебаний, для их диагностирования по вибрационным параметрам на практике можно применить следующий приём [13]. Для каждой собственной формы и частоты колебаний реального механизма устанавливается соответствие с гипотетической одномассовой системой, и реальный механизм рассматривается как набор одномассовых систем. Любые механизмы с определёнными допущениями можно представить набором одномассовых систем. Сложное входное возмущение можно представить в виде ряда Фурье, что позволяет анализировать реакцию механизма на отдельное гармоническое возмущение.
При таком подходе основная задача - это правильно определить основные (определяющие) собственные формы и частоты диагностируемого механизма. Исправное техническое состояние будет описываться характерными только для исправного объекта амплитудно-частотным составом возмущающей силы и динамическими свойствами (инерционными, жесткостными, демпфирующими) выбранных определяющих форм колебаний. Для задания неисправных технических состояний необходимо установить зависимости амплитудно-частотного состава возмущающей силы и динамических свойств определяющих форм колебаний от конкретных неисправностей механизма.
При более общем подходе реальную механическую (колебательную) систему можно представить как многомерную систему с m входами и n выходами (рис. 2.14).
F1 X1 Fj - внешняя возмущающая
: сила, действующая на j-й
Fj Xi вход системы;
A Xi - перемещение механической
: системы на i-м выходе.
Fm Xn
Рис.2.14. Упрощенное представление диагностируемого объекта в
виде многомерной колебательной системы
В этом случае оператор А представляет собой систему дифференциальных уравнений с n степенями свободы.
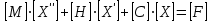. (2.16)
Если система имеет n уравнений, то симметричные матрицы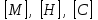
имеют размерность 
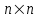и описывают соответствующие инерционные, демпфирующие и жесткостные свойства системы, а векторы [X] и [F] имеют размерность n и описывают координаты системы и возмущающие силы. Отметим, что и в этом случае диагностическая модель является неявной, что характерно для задач вибрационной диагностики.
Рассмотрим в качестве примера, как изменятся вибрационные характеристики стержня или пластины, которыми можно смоделировать вал или лопатку, при появлении трещины [14]. Представим себе балку на шарнирных опорах или с защемленным концом, у которой появилась трещина (рис. 2.15)
трещина
6 6 6 6
1 0 0 0 1 0 1 0
S0 S5 S6 S7 S4 S3 S1 S2
2
1 0
S7 S6
Рис. 2.12. Алгоритм определения состояния объекта
И функциональная модель, и граф причинно-следственных связей в конечном итоге определяют математическую модель объекта в виде таблицы состояний. Задание оператора объекта диагностирования в табличной форме достаточно удобно. Однако в ряде случаев (например, когда параметры определены на непрерывном множестве) такое представление оператора невозможно. В таких ситуациях математическая модель может быть представлена в виде аналитических зависимостей между входными возмущениями, параметрами технического состояния и диагностическими параметрами.
В технической диагностике математические (диагностические) модели объектов, устанавливающие связь между входными возмущениями, параметрами технического состояния и диагностическими параметрами (признаками) в виде аналитических зависимостей (уравнений) называются аналитическими моделями. Эти аналитические модели (зависимости) чаще всего могут быть представлены в виде алгебраических или дифференциальных уравнений. Познакомимся с некоторыми подобными моделями.
2.5 Аналитические модели в виде дифференциальных уравнений
Наиболее часто аналитические модели в виде дифференциальных уравнений применяются в вибрационной диагностике. Это связано с тем, что вибрация (упругие механические колебания) механизмов - это их реакция на действие приложенных возмущающих сил, а основным математическим аппаратом для анализа вибрации (упругих механических колебаний) технических устройств является аппарат дифференциальных уравнений [5, 7, 9, 13].
Вибрационное (колебательное) поведение технических систем описывается дифференциальным уравнением (системой уравнений), у которого (как правило) в правой части находится аналитическое выражение, определяющее зависимость возмущающих сил от времени. В левую часть этого уравнения (системы уравнений) помещены производные по времени перемещений точек механизма с коэффициентами, характеризующими инерционные (массовые), упругие (жесткостные) и демпфирующие (рассеивающие) свойства этого механизма. Отсюда следует, что анализ виброакустических процессов для целей диагностики позволяет выявить такие неисправности, которые приводят к изменению действующих на механизм возмущающих сил или к изменению инерционных, жесткостных и демпфирующих свойств этого механизма (например, разбалансировку роторов, нарушение соосности роторов, возникновение трещин, неисправности подшипниковых узлов и т.п.). Поясним это на простейшем примере.
Представим диагностируемый механизм в виде простой одномассовой колебательной системы (рис.2.13).
F(t) F(t) - возмущающая внешняя сила; m - масса системы;
m x(t) C - коэффициент жесткости системы;
h- коэффициент демпфирования в системе;
x(t)- перемещение центра масс по действием
C h возмущающей силы.
Рис. 2.13. Простейшая одномассовая колебательная система
Колебания центра масс этой системы описываются следующим дифференциальным уравнением:
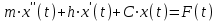. (2.9)Общее решение этого уравнения, описывающее зависимость перемещения центра масс от времени, записывается в следующем виде:
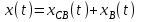, (2.10)где xСВ(t) - определяет свободные колебания цента масс, а xВ(t) - вынужденные.
Для того чтобы в ходе решения уравнения (2.9) получить конкретные аналитические зависимости от времени свободных и вынужденных колебаний, необходимо определить в конкретном аналитическом виде зависимость от времени возмущающей силы [5, 20]. При изучении вибрационных процессов чаще всего используется представление как самих колебаний, так и действующих сил в виде ряда Фурье. Поэтому примем, что возмущающая сила, действующая на систему, является гармонической (т. е.
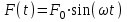, где F0 - амплитуда возмущающей силы, - частота возмущающей силы). С учетом этого выражение (2.9) можно переписать в виде 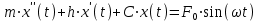. (2.11)Решая это уравнение, получим, что свободные колебания являются затухающими и определяются выражением
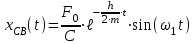, (2.12)где
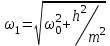- частота свободных колебаний; 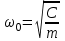- собственная частота колебаний системы. Необходимо отметить, что в реальных системах m h, поэтому свободные колебания механических систем совершаются с частотой, практически равной собственной частоте системы (т.е.
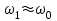). Воспроизвести свободные колебания в реальных условиях можно путем тестового воздействия на объект коротким импульсом возмущающей силы, то есть ударом. При возбуждении системы (см. рис. 2.13) ударом она будет совершать свободные колебания с частотой, равной собственной частоте системы. Амплитуда колебаний будет зависеть от соотношения между амплитудой силы и жесткостью системы. Скорость затухания колебаний будет определяться величиной соотношения демпфирования и массы в системе. Отсюда следует, что обнаружить неисправность объекта путем анализа его свободных колебаний можно в том случае, если эта неисправность вызовет изменение частоты свободных колебаний или скорости их затухания. Или, другими словами, если неисправность повлияет на динамические (жесткостные, демпфирующие, массовые) характеристики системы.
Если поведение системы описывается уравнением (2.11) и на нее постоянно действует гармоническая сила, то через определенный интервал времени свободные колебания затухнут, и система будет совершать только вынужденные колебания. Эти колебания будут также гармоническими, а их аналитическая зависимость определяется выражением
xВ(t) = X0 sin (t), (2.13)
где X0 - амплитуда вынужденных колебаний; - частота вынужденных колебаний.
Частота вынужденных колебаний равна частоте возбуждающей силы, а амплитуда колебаний зависит от амплитуды возбуждающей силы и коэффициента динамичности
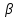:X0 = F0. (2.14)
Коэффициент динамичности зависит только от характеристик системы и для нашего случая определяется следующим соотношением:
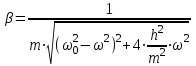(2.15) Максимальное значение коэффициент динамичности принимает при равенстве частоты возбуждающей силы собственной частоте системы: = 0. Такое явление называется резонансом, и говорят, что система совершает резонансные колебания. Как следует из соотношения (2.15), амплитуда резонансных колебаний зависит от величины возбуждающей силы и демпфирующих свойств системы.
Приведенные соотношения свидетельствуют о том, что диагностика объектов путем анализа вынужденных колебаний возможна в том случае, если неисправности вызывают изменение возбуждающей силы (ее величины или частоты) или изменение динамических свойств самого объекта (массы, жесткости, демпфирования).
Представленные выше зависимости выходного сигнала (колебаний) описыва-ют только одно техническое состояние механизма (исправное) , для получения описаний неисправных состояний необходимо установить зависимости между параметрами силы (входным воздействием) и дефектами или зависимости между массой , жесткостью, демпфированием и дефектами, то есть для вибрационной диагностики характерно задание неявных моделей.
Реальные механизмы обладают
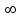числом собственных форм и частот колебаний, для их диагностирования по вибрационным параметрам на практике можно применить следующий приём [13]. Для каждой собственной формы и частоты колебаний реального механизма устанавливается соответствие с гипотетической одномассовой системой, и реальный механизм рассматривается как набор одномассовых систем. Любые механизмы с определёнными допущениями можно представить набором одномассовых систем. Сложное входное возмущение можно представить в виде ряда Фурье, что позволяет анализировать реакцию механизма на отдельное гармоническое возмущение.
При таком подходе основная задача - это правильно определить основные (определяющие) собственные формы и частоты диагностируемого механизма. Исправное техническое состояние будет описываться характерными только для исправного объекта амплитудно-частотным составом возмущающей силы и динамическими свойствами (инерционными, жесткостными, демпфирующими) выбранных определяющих форм колебаний. Для задания неисправных технических состояний необходимо установить зависимости амплитудно-частотного состава возмущающей силы и динамических свойств определяющих форм колебаний от конкретных неисправностей механизма.
При более общем подходе реальную механическую (колебательную) систему можно представить как многомерную систему с m входами и n выходами (рис. 2.14).
F1 X1 Fj - внешняя возмущающая
: сила, действующая на j-й
Fj Xi вход системы;
A Xi - перемещение механической
: системы на i-м выходе.
Fm Xn
Рис.2.14. Упрощенное представление диагностируемого объекта в
виде многомерной колебательной системы
В этом случае оператор А представляет собой систему дифференциальных уравнений с n степенями свободы.
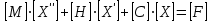. (2.16) Если система имеет n уравнений, то симметричные матрицы
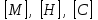имеют размерность 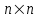и описывают соответствующие инерционные, демпфирующие и жесткостные свойства системы, а векторы [X] и [F] имеют размерность n и описывают координаты системы и возмущающие силы. Отметим, что и в этом случае диагностическая модель является неявной, что характерно для задач вибрационной диагностики. Рассмотрим в качестве примера, как изменятся вибрационные характеристики стержня или пластины, которыми можно смоделировать вал или лопатку, при появлении трещины [14]. Представим себе балку на шарнирных опорах или с защемленным концом, у которой появилась трещина (рис. 2.15)
трещина