ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 31
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
_______________________________________________________
(наименование организации образования)
Поурочный план или краткосрочный план для педагога организаций среднего образования
____________________________________________________ (тема урока)
| Раздел: | 10.4 А Производная и ее применение | |
| ФИО педагога | Мамбет М.Б | |
| Дата: | | |
| Класс: | Количество присутствующих: | Количество отсутствующих: |
| Тема урока | Критические точки и точки экстремума функции | |
| Цели обучения в соответствии с учебной программой | 10.4.1.29 - находить критические точки и точки экстремума функции; | |
| Цели урока | - знаeт необходимое и достаточное условие существования экстремума функции - находит критические точки и экстремум функции | |
Ход урока
| Этап урока/ Время | Действия педагога | Действия ученика | Оценивание | Ресурсы | ||||||||
| |
Активизация учащихся, создание ситуации успеха. Проверка домашнего задания Вопрос.Что можно сказать о наличии производной в этих точках и об ее значении? Гипотеза:в точках экстремума производная равна 0 Вопрос.Что можно сказать о наличии производной в этих точках и об ее значении? Гипотеза:в точках экстремума производная равна 0 Вопрос.Что можно сказать о наличии производной в этих точках и об ее значении? Гипотеза:в точках экстремума производная равна 0 Вопрос.Что можно сказать о наличии производной в этих точках и об ее значении? Гипотеза:в точках экстремума производная равна 0 Остановимся подробнее на точках экстремума. Вспомним определение точек максимума и минимума. Остановимся подробнее на точках экстремума. Вспомним определение точек максимума и минимума. Остановимся подробнее на точках экстремума. Вспомним определение точек максимума и минимума. Остановимся подробнее на точках экстремума. Вспомним определение точек максимума и минимума. Вопрос.Что можно сказать о наличии производной в этих точках и об ее значении? Гипотеза:в точках экстремума производная равна 0 Стратегия «Ты мне - я тебе» Задают вопросы по теоретическому материалу урока. Следит за правильностью ответов учащихся и оцениванием. Заполните таблицу. Используя геометрическую иллюстрацию, расставьте знаки производной и сделайте вывод о виде экстремума функции. Найдите экстремумы функции. a) f(x)=(x+1)2(x-2)2 b)f(x)= 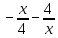 c) f(x)=- 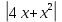 Учитель оказывает поддержку. По завершению работы сообщаются верные ответы. Задание уровня В Построим экстремумы функции и нарисуем эскиз графика данной функции (рис с искажением) Итог урока Домашнее задание:№788 (1,3) 789 (1,3) Рефлексия.
| Формулируют тему и цель урока Выполняют самопроверку домашнего задания по образцу. Отвечают на вопрос друг друга. Выполняют задание Дескриптор: Обучающийся - определяет знаки производной в интервалах; - определяет вид экстремума функции. У 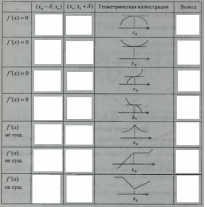 чащиеся 1 ряда выполняют задание а), 2 ряда – в), 3 ряда – с). Первый выполнивший задание записывает его на доске, остальные могут корректировать и дополнять. чащиеся 1 ряда выполняют задание а), 2 ряда – в), 3 ряда – с). Первый выполнивший задание записывает его на доске, остальные могут корректировать и дополнять.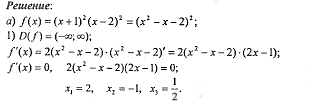 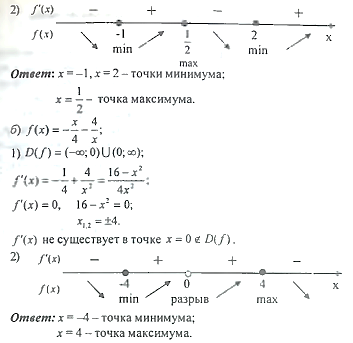 С  амостоятельная тестовая работа амостоятельная тестовая работа   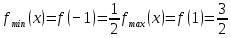 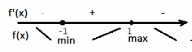 f(0)=1. f(0)=1.Отметим эти точки на координатной плоскости. З 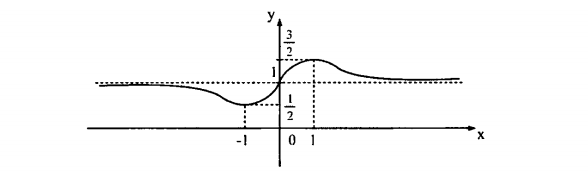 апишем функцию в виде апишем функцию в виде 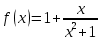 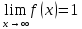 х=1 горизонтальная асимптота. х=1 горизонтальная асимптота.E(f)=[0.5;1.5] Заполняют таблицу | Оценивается правильность решения ( баллов) Взаимопроверка. проверка по образцу. Взаимопроверка. Обратная связь с учителем ФО (мах 10 баллов, за каждое по 2 балла) Обратная связь учителя | Презентация Раздаточный материал И.П. Рустюмова, Т.А. Кузнецова, С.Т. Рустюмова Пособие по подготовке к ЕНТ по математике |