1 Кбит/с = 10³ бит/с;

1 Мбит/с = 10⁶ бит/с;

1 Гбит/с = 10⁹ бит/с.

При отсутствии в канале связи помех I_s^max = log₂ n; тогда

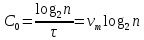(2)

– максимально возможное значение пропускной способности (это обстоятельство отражено индексом «0»). В реальном канале
I_s^max ≤log₂ n и, следовательно, C ≤C₀. Пропускной способность канала связи – максимально возможная скорость передачи по этому каналу, которая обеспечивается при источнике с максимальной энтропией. Еще раз подчеркнем, пропускная способность – характеристика канала связи. Для дискретного канала она зависит от технической скорости передачи, которая ограничивается полосой пропускания канала, и от потерь информации. Последние зависят от помех, действующих в канале, способов обработки сигналов в передатчике и приемнике, а также и от технической скорости передачи.

Скорость передачи информации. Если источник выдает ν_m элементарных сигналов в единицу времени, а средняя длина кода одного знака составляет K(A, x), то, очевидно, отношение ν_m /K(A, x) будет выражать число знаков первичного алфавита, выдаваемых источником за единицу времени. Если с каждым из них связано среднее количество информации I^(X), то можно найти общее количество информации, передаваемой источником за единицу времени — эта величина называется скоростью передачи или энтропией источника (будем обозначать ее J):

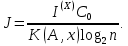(3)

Согласно первой теореме Шеннона при любом способе кодирования



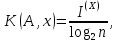
хотя может быть сколь угодно близкой к этому значению. Следовательно, всегда J ≤ C₀, т. е.

Скорость передачи информации по каналу связи не может превысить его пропускной способности.

В этом результате нет ничего неожиданного: представьте трубу, через которую за единицу времени может проходить объем воды

---

C, и источник, выдающий J воды за это же время; ясно, что если трубу присоединить к источнику, то вода не будет теряться только в том случае, если C  J.

Как показано в теории Шеннона, данное утверждение справедливо как при отсутствии в канале помех (шумов) (идеальный канал связи), так и при их наличии (реальный канал связи).

Пример. Первичный алфавит состоит из трех знаков с вероятностями p₁ = 0,2; p₂ = 0,7; p₃ = 0,1. Для передачи по каналу без помех используются равномерный двоичный код. Передача ведется на частоте 500 Гц. Каковы пропускная способность канала и скорость передачи?

Поскольку код двоичный, n = 2, а из (2) C₀ = 500 бит/с.

Число знаков первичного алфавита N = 3.

I^(X) = I₁ = −0,2 log₂ 0,2 − 0,7 log₂ 0,7 − 0,1 log₂ 0,1 = 1,16 бит,

K(A, 2) >log₂ N = 2. Следовательно, получаем

2. 
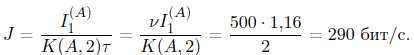
   Влияние шумов на пропускную способность дискретного канала связи
   
   1. 
      Математическая постановка задачи
      

Используем для анализа процесса передачи информации по дискретному каналу с помехами энтропийный подход.

Если считать опытом Xотправку сигнала, а Y— получение его из канала, то величина I(X, Y) выражает собой информацию, которая содержится в сигнале Xотносительно полученного сигнала Y:

I(X, Y) = H(Y) − H(Y|X).

Cледует сделать несколько замечаний.

1. Ситуация H(Y|X)= 0 (выходные сигналы совпадают с входными) соответствует идеальному каналу без помех.

2. Если Xи Yнезависимы, т. е. отсутствует связь между сигналами на входе и выходе канала, то H(Y|X)= H(Y) и информация не передается.

3. Потери информации при передаче характеризуются апостериорными вероятностями, входящими в выражение для H(Y|X)

4. Ранее было показано, что I(X, Y) = I(Y, X), т. е. Xсодержит относительно Yто же количество информации, что и Yотносительно X. Следовательно,

I(Y, X) = H(X) − H(X|Y).

(4)

Сущность задачи о передаче информации по реальному каналу состоит в том, чтобы построить заключение о том, какой сигнал

---

Xбыл отослан в случае приема Y.

Пусть опыт Yсостоит в выяснении того, какой сигнал был получен на приемном конце канала; исходами этого опыта являются сигналы y_j, общее число которых равно m. Опыт Xсостоит в выяснении того, какой сигнал был послан на вход канала; исходами этого опыта являются сигналы, образующие алфавит x_i; их общее количество равно n.

Смысл выражения (4) в применении к рассматриваемой ситуации состоит в том, что распознанный на приемном конце сигнал содержит информацию о сигнале, который был отправлен, но в общем случае информацию не полную. Влияние помех в канале таково, что в процессе передачи часть начальной информации теряется и исход опыта Yне несет полной информации относительно предшествующего исхода опыта X.

Энтропия, связанная с определением того, какой сигнал передан



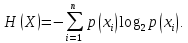
H_н(X|Y) – условная энтропия (энтропия опыта Xпри условии, что реализовался опыт Y):





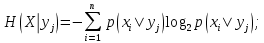
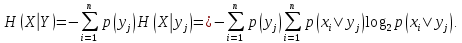
Окончательно для средней информации на один элементарный сигнал имеем (5)



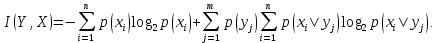
Часто бывает удобнее воспользоваться подобным же соотношением, которое получается на основе равенства

I(Y, X) = I(X, Y) = H(Y) − H_α(Y|X)

Тогда (6)



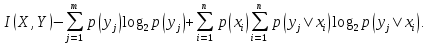
Таким образом, для определения информации сигнала на приемном конце канала необходимо знание априорных и апостериорных вероятностей. Справедливо и обратное утверждение: знание априорных и апостериорных вероятностей позволяет установить (вычислить) информацию, связанную с переданным сигналом.

Как уже указывалось, апостериорные вероятности определяются свойствами канала связи, а априорные – особенностями источника (точнее, кодера). Следовательно, воспользовавшись (5) или (6) и варьируя значения p(a_i) в допустимых по условию задачи пределах, можно найти наибольшее значение max{I(Y, X)}. Тогда

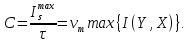(7)

Полученное выражение определяет порядок решения задачи о нахождении пропускной способности конкретного канала:

---

1) исходя из особенностей канала, определить априорные и апостериорные вероятности;

2) варьируя p(x_i) и пользуясь (5), найти максимальное информационное содержание элементарного сигнала;

3) по (7) вычислить пропускную способность.

Пример.

Пусть в канале отсутствуют помехи или они не препятствуют передаче. Тогда m = n, сигналы на приемном конце совпадают с отправленными. Это означает, что апостериорные вероятности p(x_i|y_j) = 1 при i = j и p(y_j|x_i) = 0 при i  j. B этом случае H(X|Y) = 0 и, следовательно, max{I(Y, X)}= = max{H(X)}= log₂ n (это значение достигается, если появление всех входных сигналов равновероятно). Из (6) получаем C = ν_m log₂ n, что совпадает с (3). Тем самым показано, что определение (3) пропускной способности канала без помех является частным случаем более общего определения (6).

Рассмотрим некоторые примеры каналов передачи информации с помехами.

2. 
   Однородный двоичный симметричный канал
   

Пусть на вход канала подаются сигналы двух типов (0 и 1 — например, импульс и пауза) и они же принимаются на выходе, т. е. {x}= {b}, m = n. Пусть, далее, вероятность ошибки передачи для обоих сигналов одинакова и равна p; такой канал называется двоичным симметричным (относительно инверсии 0 ↔ 1). Если вероятность ошибки p, то для дополнительных событий вероятность безошибочной передачи равна 1 − p.

Применяя принятые выше обозначения для апостериорных вероятностей, можно записать

p₀(1) = p₁(0) = p; p₀(0) = p₁(1) = 1 − p,

Этим соотношениям может быть дана графическая интерпретация (рис. 3) (он называется графом канала). Линии со стрелками указывают, в какие принимаемые сигналы могут перейти те, что отправлены на входе; рядом со стрелками указаны вероятности соответствующих переходов.

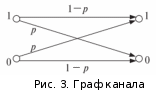Найдем пропускную способность канала, воспользовавшись определением (7). Оно, в свою очередь, требует вычисления I(Y, X) (или I(X, T)) и установления ее максимума как функции p. Если по-прежнему опыт Xсостоит в распознавании сигнала на входе канала, а опыт Y— на выходе, с учетом того, что y₁ = x₁, а y₂ = x₂, и воспользовавшись выражением (6), получаем

---

H₀(Y) = H₁(Y) = −(1−p) log₂(1−p)−p log₂ p.

и

H(Y|X) = p(0)H₀(Y) + p(1)H₁(Y) =
= {p(0) + p(1)}{−(1 − p) log₂(1−p)−p log₂ p}=
= −(1−p) log₂(1−p)−plog₂ p,

поскольку p(0)+p(1) = 1 как достоверное событие. Другими словами, в рассматриваемом канале энтропия H(Y|X) не зависит от значений p(0) и p(1), а определяется только вероятностью искажений сигнала при передаче. Следовательно,

C = ν_m max{H(Y)+(1−p) log₂(1−p) + p log₂ p}.

Поскольку m=2, max{H(Y)}= 1. Таким образом, окончательно для пропускной способности симметричного двоичного канала имеем

C(p) = ν_m{1 + (1 − p) log₂(1 − p) + p log₂ p}.

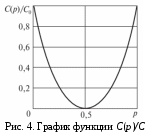График функции C(p)/C₀ изображен на рис. 4. Максимального значения равного ν_m функция C(p) достигает при p = 0 (очевидно, это означает отсутствие помех) и при p = 1 — это соответствует ситуации, когда канал полностью инвертирует входные сигналы (т.е. заменяет 0 на 1, а 1 на 0) — это не служит препятствием для однозначной идентификации посланного сигнала по принятому и, следовательно, не снижает пропускной способности канала. Во всех остальных ситуациях 0
1 и C(p)<ν_m. Наконец, при p=0,5 пропускная способность становится равной 0 – это вполне естественно, поскольку вероятность искажения 0,5 соответствует ситуации, при которой независимо от того, какой сигнал был послан, на приемном конце с равной вероятностью может появиться любой из двух допустимых сигналов. Ясно, что передача в таких условиях оказывается невозможной.

Поскольку канал двоичный, согласно (3) ν_m = C₀. Проведя соответствующую замену, получим

C = C0{1+(1−p) log2(1−p)+p log2 p}.

(8)

Выражение в фигурных скобках не превышает 1, следовательно, справедливо соотношение C  C₀, т.е. можно считать доказанным, что наличие помех снижает пропускную способность (и даже может сделать ее равной 0).

Пример.

Каково отношение C/C₀, если средняя частота появления ошибки при передаче сообщения в двоичном симметричном канале составляет 1 ошибочный сигнал на 100 переданных?

Очевидно, вероятность появления ошибки передачи p = 0,01. Следовательно, из (8) получаем

C/C₀ = 1 + p log₂ p + (1 − p) log₂(1 − p) ≈ 0,9192,

т. е. пропускная способность канала снизилась приблизительно на 8 %. Следует заметить, что отношение C/C₀ убывает при увеличении вероятности искажения довольно быстро, что иллюстрируется таблицей:



Отдельно следует обсудить вопрос, каким образом может быть установлен факт, что канал является симметричным и как определить вероятность искажения. Эти данные не вытекают ни из какой теории и могут быть получены только опытным путем.

На вход в канал подаются большое количество (для обеспечения заметной статистики) чередующихся сигналов 0 и 1 (рис. 5), а на приемных концах подсчитывается, сколько пришло тех или иных сигналов. Если число искаженных сигналов на обоих приемных концах одинаково (близко), то можно делать вывод о симметричности канала. Отношение количества искаженных (ошибочных) импульсов к числу отправленных, очевидно, даст вероятность искажения.

2. 
   Однородный симметричный канал со стиранием
   

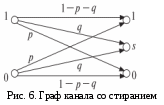
Снова рассмотрим двоичный канал (на входе сигналы 0 и 1 с вероятностями появления p(0) и p(1) соответственно). Допустим, что на приемном конце любой из них с вероятностью p может быть интерпретирован как противоположный, но, помимо этого, с вероятность q искажения в канале оказываются такими, что из-за конечной точности приемника принятый знак не идентифицируется ни с одним из поступающих на вход.

B таком случае можно считать, что принят новый сигнал s, появление которого следует интерпретировать как пропажу (стирание) входного сигнала (как если бы при переписывании мало разборчивого текста все непонятные буквы мы заменяли бы каким-то знаком) – по этой причине канал назван двоичным симметричным со стиранием. По-видимому, вероятность стирания q > p, поскольку это событие требует меньшего искажения исходного сигнала, чем его инверсия.

Апостериорные вероятности в этом случае составят:

p₀(0) = p₁(1) = 1 − p − q; p₀(1) = p₁(0) = p; p₀(s) = p₁(s) = q.

Граф канала будет показан на рис. 6.

Для определения пропускной способности вновь, как и при решении предыдущей задачи, воспользуемся соотношением (6).

Расчет условной энтропии дает:

H₀(y) = H₁(y)=−(1−p−q) log₂(1−p−q)−plog₂ p−qlog₂ q;

H(Y|X) = p(0)H₀(y)+p(1)H₁(y) =

= {p(0) + p(1)}{−(1 − p − q) log₂(1 − p − q) − p log₂ p − q log₂ q}=
= {−(1−p−q) log₂(1−p−q)−p log₂ p−q log₂ q};

вновь учтено, что p(0)+p(1) = 1 как достоверное событие. Таким образом,

I(X, Y) = H(X)+(1−p−q) log₂(1−p−q)−p log₂ p−q log₂ q.

Поскольку H (Y|X) не зависит от значений априорных вероятностей, I(X, Y) достигает максимума при таких p(0) и p(1), когда наибольшее значение приобретает энтропия H(Y). Для нахождения H(Y) необходимо знать вероятности всех сигналов, появляющихся на выходе из канала (обозначим эти вероятности q_j, j = 0, 1, 2).

Вероятность появления s (стирания) уже установлена: q₂ = q. Для 0 вероятность q₀ =p(0)(1−p−q)+p(1)p; аналогично для 1 находим q₁ = p(1)p + p(1)(1−p−q). Тогда

H(Y) = −q₁ log₂(q₁)−q₂ log₂ q₂ −q log₂ q.

Поскольку q определяется особенностями канала и не зависит от априорных вероятностей сигналов на входе, наибольшим H(Y) будет при максимальном значении выражения −q₁ log₂ q₁ −q₂ log₂ q₂, причем при любых p(0) и p(1) справедливо q₁ + q₂ = = 1 − q. Можно показать, что указанное выражение достигает максимума при условии q₁ = q₂ = 0,5(1 − q). Тогда





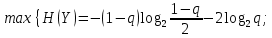
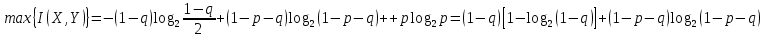
Окончательно для пропускной способности двоичного симметричного канала со стиранием имеем

C = ν_m{(1−q)[1−log₂(1−q)]+(1−p−q) log₂(1−p−q) + p log₂ p}.

Проанализируем полученный результат C = C(p, q): C будет уменьшаться при увеличении как p, так и q. Если вероятности p и q отличны от 0, то, как видно из полученного выражения, C < C₀.

В реальных двоичных каналах со стиранием p, т. е. вероятность такого искажения входного сигнала, при котором его невозможно распознать, выше вероятности такого искажения, при котором сигнал становится похожим на второй из используемых сигналов.

В тех ситуациях, когда p пренебрежимо мала и единственным искажением оказывается стирание сигнала, пропускная способность оказывается равной C=ν_m(1−q). График этой функции представлен на рис. 7.

Полученный результат представляется вполне закономерным: при p = 0 из ν_m двоичных сигналов, передаваемых по каналу за единицу времени, в среднем ν_mq будет «стираться», но при этом остальные ν_m(1−q) сигналов будут на приемном конце расшифровываться без потерь, и с каждым из них связан ровно 1 бит информации.

Заканчивая рассмотрение характеристик реального дискретного канала передачи информации, следует сделать следующие заключения.

1. Помехи, существующие в реальном канале связи, приводят к снижению его пропускной способности (по сравнению с аналогичным каналом без помех).

2. Пропускная способность реального канала может быть рассчитана по известным априорным и апостериорным вероятностям. Для их определения требуются статистические исследования передачи информации в канале.

2. 
   Модель потоков ошибок в дискретном канале
   

5.1 Общая характеристика моделей потоков ошибок
Вектором ошибки называют поразрядную разность (для двоичного сигала по mod₂) между принятой кодовой комбинацией Bⁿ и переданной Aⁿ:

mod_m (AⁿBⁿ)Eⁿ,

тогда

Bⁿ= mod_m(Eⁿ+ Aⁿ)

При передаче двоичным кодом кодовые комбинации представляют совокупность 0 и 1, а суммирование производится по модулю 2.
Двоичный симметричный канал представляют как сумматор по модулю 2, к которому подключены источник сообщений и источник ошибок. Оба источника выдают двоичные последовательности длиной n. Будем обозначать символы в последовательности ошибок e_i. Каждый элемент последовательности {e} складывается с соответствующим элементом последовательности, поступающей от источника сообщений {a}, в двоичном канале по модулю 2 (рис. 8).
В дискретных каналах различают

– r-кратные ошибки (каналы с независимыми ошибками);

– пакеты ошибок (зависимые или группирующиеся ошибки).

Пакеты – это последовательность нескольких искажённых символов:

B = A + e,

если е = 0 – ошибки нет, если е = 1 – есть ошибка.

Число ошибочных элементов определяет вес вектора ошибок ||E||.

Пример. Пусть на вход ДК поступает последовательность 10011011, на выходе имеем последовательность 11010111. Вывод: на передаваемый сигнал воздействовала некоторая помеха, что привело к искажению. Отдельных символов. Математически это записывается следующим образом:

10011011 – вектор входного сигнала а_i

01001000 – вектор ошибки e_i

11010111 – вектор выходного сигнала b_i

Число ошибочных элементов определяет вес вектора ошибок. Для рассматриваемого примера вес вектора ошибок ||E||=2.

Группа ошибок, ограниченная двумя крайними ошибочными элементами, называется пакетом (пачкой) ошибок.

Длина L пачки ошибок – важный параметр, так как его используют при выборе помехоустойчивых кодов.

В примере на рис. 9 L=5.

Если ошибки при приёме отдельных символов кодовой комбинации происходят независимо друг от друга c вероятностью p, то вероятность безошибочного приёма кодовой комбинации из n элементов будет равна (1-p)ⁿ , а вероятность ошибочного её приёма равна значению 1-(1-p)ⁿ. Вероятность одновременного числа ошибок t в информационной последовательности определяется значением p^t . Вероятность того, что в комбинации, имеющей n разрядов, n–t элементов не искажены, составляет (1-p)^n–t . Следовательно, вероятность одного заданного сочетания ошибок t в nразрядной последовательности составляет величину p^t (1-p)^n–t.

Общее количество возможных комбинаций t-кратных ошибок в n-разрядной комбинации составляет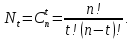



Отсюда вероятность наличия в комбинации из n разрядов t ошибок в любом сочетании равна

=

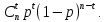
При независимом распределении ошибок свойства канала по выходу как источника ошибок {e_i} задаются единственным параметром – вероятностью ошибки р на символ.

Кроме независимых ошибок в канале могут возникать группирующиеся ошибки. Они образуются в каналах с памятью. Одной из основных причин таких ошибок являются перерывы, возникающие из-за плавного снижения уровня сигнала ниже порога чувствительности приёмника, когда приём сигнала фактически прекращается. Перерывы могут быть различной длительности, и некоторые из них способны даже вызывать прекращение сеанса связи. Кроме этого, причиной перерывов могут быть неисправности в аппаратуре, несовершенство её эксплуатации, проведение измерений и др. Перерывы и импульсные помехи являются основной причиной появления группирующихся ошибок при передаче дискретных сообщений по различным видам каналов связи. Импульсные помехи – это помехи, сосредоточенные по времени. Они представляют собой случайную последовательность импульсов, имеющих случайные амплитуды и следующих друг за другом через случайные интервалы времени, причём вызванные ими переходные процессы, не перекрываются во времени. Причины появления этих помех: коммутация соединений в электронной аппаратуре, наводки с высоковольтных линий, грозовые разряды, прием отраженных сигналов и т.п.

---

Смотрите также файлы

• Дисциплина Информатика и информационнокоммуникационные технологии в профессиональной деятельности Практическое занятие 4 Обучающийся Уланова Александра Александровна Преподаватель Афанасьева Ирина Эриковна.doc

• Натуральный ряд чисел. 5 класс, умк а. Г. Мерзляк, В. Б. Полонский и др.docx

• Исследование ценностей национальнокультурной самостоятельности в отдельных социальнодемографических группах населения России.docx

• Характеристики дискретного канала связи Влияние шумов на пропускную способность дискретного канала связи Однородный двоичный симметричный канал.pptx

• Солнце огромный пылающий шар. Большая Медведица.docx